基于非负矩阵分解的多视图聚类方法、系统、设备及介质

本技术涉及多视图聚类，尤其是涉及一种基于非负矩阵分解的多视图聚类方法、系统、设备及介质。

背景技术：

1、随着多视图数据在许多现实应用中变得越来越普遍，学习多视图数据是机器学习研究中的一个新兴问题。例如，多组类数据现在无处不在，可以从同一对象中获得不同的信息类型，例如纹理信息、 形状信息，颜色信息等。在这些场景中，同一组对象具有通过不同测量方法或方式收集的不同视图，其中任何特定的单视图数据可能不足以全面描述所有对象的信息。因此，多视图无监督学习的一个主要目标是寻找跨视图的共识聚类使得相似的对象被分组到同一簇中，而不相似的对象被分成不同的簇中。

2、现有的相关方法通过不同应用驱动的不同目标函数来解决这个问题。然而，大多数现有的多视图nmf相关方法要么仅仅对视图权重进行定义，而忽视单个视图中不同特征的有效性，要么在推导共识聚类时先验已知特定特征的权重。在实践中，这样的假设可能无效，因为数据集往往特征量庞大且具有许多嘈杂特征。由于这些嘈杂特征可能会导致聚类错误，因此，现有的相关方法聚类效果较差。

技术实现思路

1、本技术旨在提出一种基于非负矩阵分解的多视图聚类方法、系统、设备及介质，能够提高聚类结果的准确性，从而提高聚类效果。

2、第一方面，本技术实施例提供了一种基于非负矩阵分解的多视图聚类方法，所述方法包括：

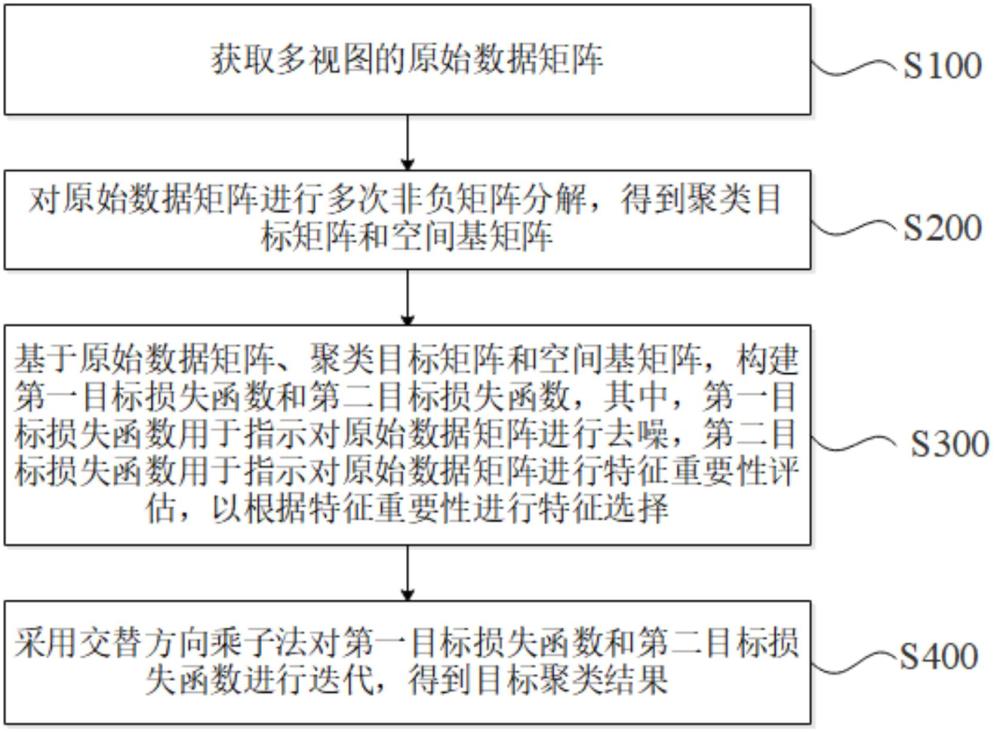
3、获取多视图的原始数据矩阵；

4、对所述原始数据矩阵进行多次非负矩阵分解，得到聚类目标矩阵和空间基矩阵；

5、基于所述原始数据矩阵、所述聚类目标矩阵和所述空间基矩阵，构建第一目标损失函数和第二目标损失函数，其中，所述第一目标损失函数用于指示对所述原始数据矩阵进行去噪，所述第二目标损失函数用于指示对所述原始数据矩阵进行特征重要性评估，以根据所述特征重要性进行特征选择；

6、采用交替方向乘子法对所述第一目标损失函数和所述第二目标损失函数进行迭代，得到目标聚类结果。

7、与现有技术相比，本技术第一方面具有以下有益效果：

8、本方法通过对原始数据矩阵进行多次非负矩阵分解，得到聚类目标矩阵和空间基矩阵；基于原始数据矩阵、聚类目标矩阵和空间基矩阵，构建第一目标损失函数和第二目标损失函数，其中，第一目标损失函数用于指示对原始数据矩阵进行去噪，第二目标损失函数用于指示对原始数据矩阵进行特征重要性评估，以根据特征重要性进行特征选择，由于原始数据矩阵中往往包含各种非线性和非高斯噪声与异常值，因此通过第一目标损失函数对原始数据矩阵进行去噪，能够很好的降低高维数据的复杂噪声对聚类结果的影响，增强了聚类过程的鲁棒性；同时通过第二目标损失函数对原始数据矩阵进行特征重要性评估，然后根据特征重要性进行特征选择，能够提高聚类的正确性。采用交替方向乘子法对第一目标损失函数和第二目标损失函数进行迭代，采用交替方向乘子法能够提高收敛速度，并且收敛性能好，并且能够在收敛之后，根据加权直接得出聚类结果，提高了聚类效果。

9、在一些实施方式中，所述基于所述原始数据矩阵、所述聚类目标矩阵和所述空间基矩阵，构建第一目标损失函数和第二目标损失函数，包括：

10、构建特征比例因子矩阵；

11、通过所述空间基矩阵约束所述聚类目标矩阵和所述原始数据矩阵的关系，以及，通过约束所述空间基矩阵、所述聚类目标矩阵和所述原始数据矩阵的非负性，构建引入所述特征比例因子矩阵的第一目标损失函数；

12、通过范数对所述原始数据矩阵和所述聚类目标矩阵进行约束，构建引入所述特征比例因子矩阵的第二目标损失函数。

13、在一些实施方式中，通过如下方式构建特征比例因子矩阵：

14、

15、其中，表示特征比例因子矩阵在第j行第j列的特征比例因子，表示特征比例因子矩阵在第j列的元素，表示聚类目标矩阵第j行的元素，表示聚类目标矩阵的总行数，表示范数。

16、在一些实施方式中，通过如下方式构建引入所述特征比例因子矩阵的第一目标损失函数：

17、

18、其中，表示原始数据矩阵，表示特征比例因子矩阵，表示聚类目标矩阵，表示空间基矩阵，表示转置，表示超参数，表示范数。

19、在一些实施方式中，通过如下方式构建引入所述特征比例因子矩阵的第二目标损失函数：

20、

21、其中，和表示可调超参数，表示原始数据矩阵，表示特征比例因子矩阵，表示聚类目标矩阵，表示损失项，表示元素全为1的向量，表示范数。

22、在一些实施方式中，所述采用交替方向乘子法对所述第一目标损失函数和所述第二目标损失函数进行迭代，得到目标聚类结果，包括：

23、将所述第一目标损失函数和所述第二目标损失函数相加，得到总损失函数；

24、将所述特征比例因子矩阵、所述聚类目标矩阵和所述原始数据矩阵输入总损失函数，采用交替方向乘子法对所述总损失函数进行迭代，得到目标聚类结果。

25、在一些实施方式中，所述将所述特征比例因子矩阵、所述聚类目标矩阵和所述原始数据矩阵输入总损失函数，采用交替方向乘子法对所述总损失函数进行迭代，得到目标聚类结果，包括：

26、将所述特征比例因子矩阵、所述聚类目标矩阵和所述原始数据矩阵中任一个参数作为变量，另外两个参数作为常量；

27、将所述变量和所述常量输入总损失函数，采用交替方向乘子法对所述总损失函数进行循环迭代，直到达到预设条件，得到目标聚类结果。

28、第二方面，本技术实施例还提供了一种基于非负矩阵分解的多视图聚类系统，所述系统包括：

29、数据矩阵获取单元，用于获取多视图的原始数据矩阵；

30、非负矩阵分解单元，用于对所述原始数据矩阵进行多次非负矩阵分解，得到聚类目标矩阵和空间基矩阵；

31、损失函数构建单元，用于基于所述原始数据矩阵、所述聚类目标矩阵和所述空间基矩阵，构建第一目标损失函数和第二目标损失函数，其中，所述第一目标损失函数用于指示对所述原始数据矩阵进行去噪，所述第二目标损失函数用于指示对所述原始数据矩阵进行特征重要性评估，以根据所述特征重要性进行特征选择；

32、聚类结果获得单元，用于采用交替方向乘子法对所述第一目标损失函数和所述第二目标损失函数进行迭代，得到目标聚类结果。

33、第三方面，本技术实施例还提供了一种电子设备，包括至少一个控制处理器和用于与所述至少一个控制处理器通信连接的存储器；所述存储器存储有可被所述至少一个控制处理器执行的指令，所述指令被所述至少一个控制处理器执行，以使所述至少一个控制处理器能够执行如上所述的一种基于非负矩阵分解的多视图聚类方法。

34、第四方面，本技术实施例还提供了一种计算机可读存储介质，所述计算机可读存储介质存储有计算机可执行指令，所述计算机可执行指令用于使计算机执行如上所述的一种基于非负矩阵分解的多视图聚类方法。

35、可以理解的是，上述第二方面至第四方面与相关技术相比存在的有益效果与上述第一方面与相关技术相比存在的有益效果相同，可以参见上述第一方面中的相关描述，在此不再赘述。