一种基于层次分析法的探头选型分析方法与流程

本发明属于盾构施工，具体涉及一种基于层次分析法的探头选型分析方法。

背景技术：

1、近年来，随着我国基础设施建设的快速发展，盾构技术在推动地铁快速建设方面发挥了重要作用。目前，主流的盾构类型包括土压平衡盾构和泥水平衡盾构。其中，渣土作为土压平衡盾构压力平衡的媒介，一方面可以平衡前方掌子面的水土压力，防止土体失稳；另一方面可以平衡螺机压力，保证设备顺利出渣。因此，往往需要通过渣土改良使渣土具有良好的流动性、合适的塑性、较低的抗剪强度和黏附强度、较小的渗透系数和一定的压缩性，从而便于排土和控制土舱压力降低刀盘结泥饼、刀具磨损、螺机喷涌的风险。

2、目前不同学者使用的试验仪器和评价指标各不相同，目前缺乏统一的评价标准；此外，由于缺乏盾构智能化方面的深入研究与工程实践，盾构掘进过程中渣土改良状态信息获取滞后，决策控制依赖人为经验致使盾构盲目掘进，导致渣土改良策略与地层条件不适应、掘进效率低等问题一直存在，因此，有必要研发一款盾构渣土改良效果评价机器人，用于渣土实时取样与检测，并结合掘进参数，指导改良参数的快速调整。机器人与试验台皆通过安装在其上的搅拌装置搅拌渣土，检测搅拌探头插入渣土时的贯入阻力以及探头旋转时的转矩，从而评价渣土的塑流性。

3、搅拌探头作为机器人与试验台中直接与渣土接触的装置，其形状决定了所测贯入阻力与转矩的敏感性，对不同形状搅拌探头贯入渣土以及搅拌过程进行仿真，并在数值模拟结果的基础上利用层次分析法对不同形状搅拌探头测量的搅拌转矩与贯入阻力敏感性进行分析，为机器人与试验台的研发应用提供帮助，是一项具有实用意义的工作。

技术实现思路

1、为了克服现有技术中的技术问题，本发明提供了一种基于层次分析法的探头选型分析方法，运用层次分析法计算各重要因素的权重值，对权重值进行评分得到影响评分，并根据搅拌探头的综合评分进行排序，最后可根据工程实际选取更利于该工程的搅拌探头，解决了上述技术问题。

2、本发明设计了一种基于层次分析法的探头选型分析方法，将带入既有数据进行分析，主要包括以下步骤：

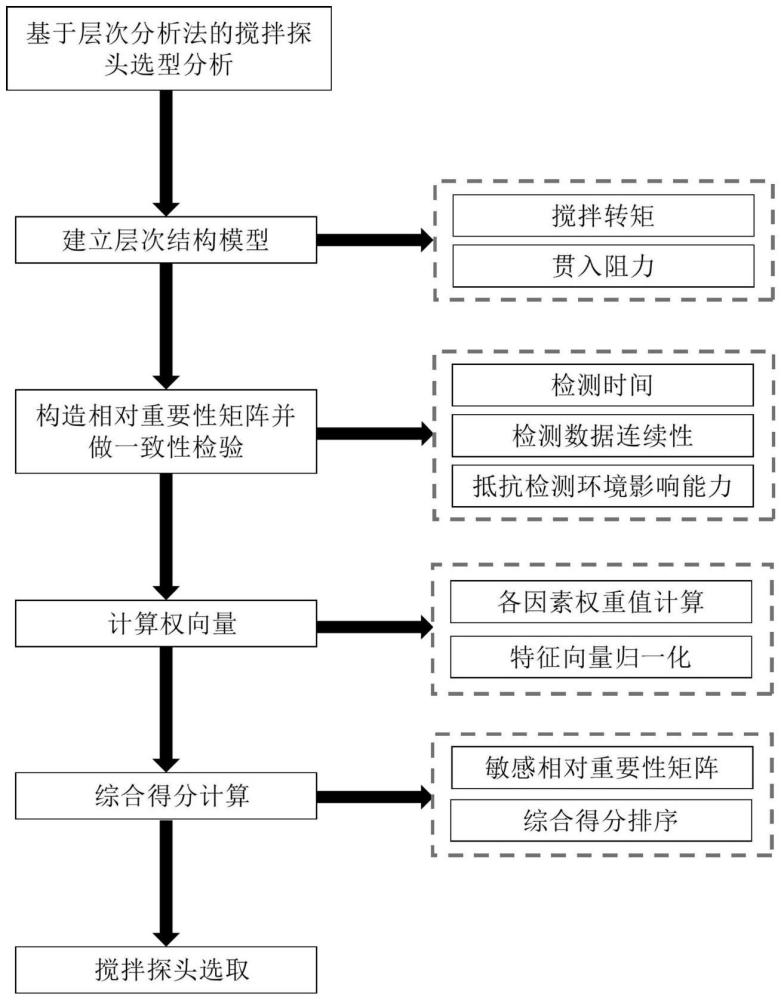
3、s1：建立层次结构模型；

4、s2：构造相对重要性矩阵并做一致性检验；

5、s3：计算权量；

6、s4：综合得分计算。

7、上述的一种基于层次分析法的探头选型分析方法，所述步骤s1中对于搅拌探头选型而言，对备选型号的多个测搅拌探头按照搅拌转矩、贯入阻力2个选型标准构建层次结构模型。

8、上述的一种基于层次分析法的探头选型分析方法，所述步骤s1中探头搅拌转矩、贯入阻力可根据数值模拟取得。

9、上述的一种基于层次分析法的探头选型分析方法，所述步骤s2中结合风险权重评价分值表以及搅拌转矩和贯入阻力两两对比结果建立相对重要性矩阵a；

10、上述的一种基于层次分析法的探头选型分析方法，所述步骤s2中风险权重评价分值表如下：

11、

12、

13、上述的一种基于层次分析法的探头选型分析方法，所述步骤s2中影响搅拌探头选型的主要因素是搅拌转矩与贯入阻力，但是考虑到检测时间、检测数据连续性、抵抗检测环境影响能力等因素，对于搅拌探头来说搅拌转矩的重要性要稍大于贯入阻力。

14、上述的一种基于层次分析法的探头选型分析方法，所述步骤s2中成对比较法把所有有关因素进行两两比较根据重要性风险评价分值表给出风险权重分值aij，则相对重要性矩阵a为：

15、

16、ij的范围为1至n，n为有关因素的个数，本发明主要考虑探头的搅拌转矩和贯入阻力两个因素，因此n＝2。

17、上述的一种基于层次分析法的探头选型分析方法，所述步骤s2中搅拌转矩和贯入阻力两两对比结果如下，相对重要性矩阵为

18、

19、 i/j 搅拌转矩 贯入阻力 搅拌转矩 1 3 贯入阻力 1/3 1

20、上述的一种基于层次分析法的探头选型分析方法，所述步骤s2中计算相对重要性矩阵a的最大特征值λmax和归一化特征向量βa，计算方法如下：

21、

22、

23、上述的一种基于层次分析法的探头选型分析方法，所述步骤s2中对所求相对重要性矩阵a需进行判断是否具有满意一致性，若计算结果ci≤0.1时则满足具有满意一致性，反之则需要重新构建相对重要性矩阵，其判断公式如下：

24、

25、式中n为矩阵的阶数。

26、上述的一种基于层次分析法的探头选型分析方法，所述步骤s2中由公式可求得λmax(a)＝2，βa＝(0·75，0·25)t，ci＝0，故得到搅拌转矩的权重为0.75，贯入阻力的权重值为0.25。

27、上述的一种基于层次分析法的探头选型分析方法，所述步骤s3中分别计算各探头搅拌转矩敏感性权重和贯入阻力敏感性权重。

28、上述的一种基于层次分析法的探头选型分析方法，所述步骤s3中转矩和贯入阻力随黏度变化曲线斜率是评价搅拌探头转矩敏感度的重要标准，可通过数值模拟取取得不同搅拌探头转矩和贯入阻力随黏度变化曲线斜率：

29、 探头型号 转矩随黏度变化曲线斜率 贯入阻力随黏度变化曲线斜率 探头1 <![cdata[b₁]]> <![cdata[c₁]]> 探头2 <![cdata[b₂]]> <![cdata[c₂]]> 探头3 <![cdata[b₃]]> <![cdata[c₃]]> ..... ..... ..... 探头n <![cdata[b_n]]> <![cdata[c_n]]>

30、上述的一种基于层次分析法的探头选型分析方法，所述步骤s3中转矩和贯入阻力的相对重要性归一化矩阵β2和β3以及最大特征值λ2max和λ3max可由权利要求11所给公式计算，相对重要性矩阵β21和β31为：

31、β21＝(b1 b2 b3 .... b5)t

32、β21＝(c1 c2 c3 .... c5)t

33、上述的一种基于层次分析法的探头选型分析方法，所述步骤s3中本发明既有转矩和贯入阻力随黏度变化曲线斜率数据如下：

34、 探头型号 转矩随黏度变化曲线斜率 贯入阻力随黏度变化曲线斜率 探头b1 2.076 0.210 探头b2 1.670 0.142 探头c2 3.434 0.212 探头p2 1.288 0.390 探头s1 1.120 0.542

35、上述的一种基于层次分析法的探头选型分析方法，所述步骤s3中既有转矩和贯入阻力随黏度变化曲线斜率数据如下可求得最大特征值λ2＝5，λ3＝5，归一化特征向量为：

36、β2＝(0.217，0.174，0.358，0.134，0.117)t

37、β3＝(0.140，0.095，0.142，0.261，0.362)t。

38、上述的一种基于层次分析法的探头选型分析方法，所述步骤s3中既有转矩和贯入阻力随黏度变化曲线斜率数据如下可求得最大特征值λ2max＝5，λ3max＝5，归一化特征向量：

39、β1＝(0.217，0.174，0.358，0.134，0.117)t

40、β2＝(0.140，0.095，0.142，0.261，0.362)t。

41、上述的一种基于层次分析法的探头选型分析方法，所述步骤s4中通过计算所得相对重要性矩阵βa，β2，β3转矩和贯入阻力对应权重值乘其对应权向量再求和即可的得到对应探头的综合得分，根据综合得分选取更贴合工程实际的探头。

42、上述的一种基于层次分析法的探头选型分析方法，所述步骤s4中通过既有数据计算综合得分如下：

43、β1＝(0.75，0.25)t

44、β1＝(0.217，0.174，0.358，0.134，0.117)t

45、β2＝(0.140，0.095，0.142，0.261，0.362)t

46、则b1探头综合得分为0.75×0.217+0.25×0.140＝0.198，同理可求得各个探头的得分如下。

47、 探头型号 转矩(权重0.75) 贯入阻力(权重0.25) 综合得分 探头b1 0.217 0.140 0.198 探头b2 0.174 0.095 0.154 探头c2 0.358 0.142 0.304 探头p2 0.134 0.261 0.166 探头s1 0.117 0.362 0.178

48、上述的一种基于层次分析法的探头选型分析方法，所述步骤s4中根据各探头的综合得分对各探头进行排序分级，最后选取适合工程实际的探头。

49、总体而言，通过本发明所构思的以上技术方案与现有技术相比，可以达到以下有益效果：本发明一种基于层次分析法的探头选型分析方法，利用层次分析法对搅拌探头进行选型分析，得到可以同时兼顾贯入阻力与搅拌转矩检测灵敏度要求的搅拌探头，为机器人与试验台的研发应用提供帮助，提高掘进施工效率，节约了工期，有效降低了施工成本和施工难度。