一种非线性液体晃动的半解析数值仿真方法、介质及终端

本发明属于数值仿真，尤其涉及一种非线性液体晃动的半解析数值仿真方法、介质及终端。

背景技术：

1、为加快建设国家现代化高质量水利基础设施网络，统筹解决水资源、水生态、水环境、水灾害问题，保障国家水安全重大战略部署的顺利开展，我国近年来实施了一系列重大调水工程，其中南水北调工程已成为优化水资源配置、畅通南北经济循环的生命线。渡槽作为南水北调工程中的关键交叉建筑，关乎整条供水线路的安全运行，南水北调渡槽多位于我国7度以上的高地震烈度地区，面临着极端地震、大风、洪水等灾害的巨大威胁，据统计，自1974年至2023年底，我国就有20余次渡槽破坏案例，其中地震破坏3例，风致破坏5例，造成此类破坏的主要原因是在地震或大风的作用下储液结构产生震动，进而引起内部液体晃动，如果外部激励频率与液体固有晃动频率接近，液体与结构之间极易产生共振现象，加之渡槽内部水体质量巨大，往往是结构自身重量的很多倍，最终可能造成整个系统的倾覆、垮塌、失稳、破坏。

2、针对这些问题，现有研究对水体的考虑一般采用理想状态下的westergaard模型和housner弹簧-质量模型，前者假设结构的振动频率远高于液体，认为流体对结构的作用是均匀分布的，忽略了局部效应，难以模拟流体对结构的局部影响；而housner模型引入水体附加质量的同时，增加了弹簧刚度模型，但housner模型难以描述液体晃动的高度非线性动力学行为，分析结果普遍偏小，且无法模拟渡槽扭转变形，在渡槽基础刚性较大时失效，导致现有数值仿真方法结果精度和效率偏低，同时，现有数值仿真方法需要域内离散，网格更新繁琐，计算成本高。公开号为cn105928677a的专利申请提供了异形水箱结构液体晃动频率测试方法，包括选取或者制作待测液体晃动频率的异形水箱结构。在液体深度范围内布置孔隙水压力传感器。向异形水箱结构中注水，使水面达到目标高度。将盛水的异形水箱结构固定在振动台上。通过数据线连接孔隙水压力传感器和高速静态应变测试分析系统，高速静态应变测试分析系统和计算机。振动台启动给异形水箱结构提供外界激励，将记录到的动水压力时程曲线进行降噪处理。提取时程曲线中液体自由晃动阶段的数据信息。将数据曲线进行fourier变换，从小到大记录每一个幅值纵坐标出现极大值时对应的横坐标频率，频率数值即为该水箱结构液体晃动的第i阶频率。此方案当中的理论推导也是基于housner理论进行分析，存在与现有技术当中相同的弊端。

3、因此，如何提供一种精确度和效率高的同时，成本也较低的液体晃动研究方法，是本技术领域人员亟待解决的问题。

技术实现思路

1、针对现有技术的不足，本发明的目的是提供一种非线性液体晃动的半解析数值仿真方法，以解决现有技术当中对液体晃动行为研究分析结果精确度和效率偏低的同时，成本也较高的问题；另外本发明还提供了一种非线性液体晃动的半解析数值求解介质及终端。

2、为了解决上述技术问题，本发明采用了如下的技术方案：

3、第一方面，本发明提供了一种非线性液体晃动的半解析数值仿真方法，包括以下步骤：

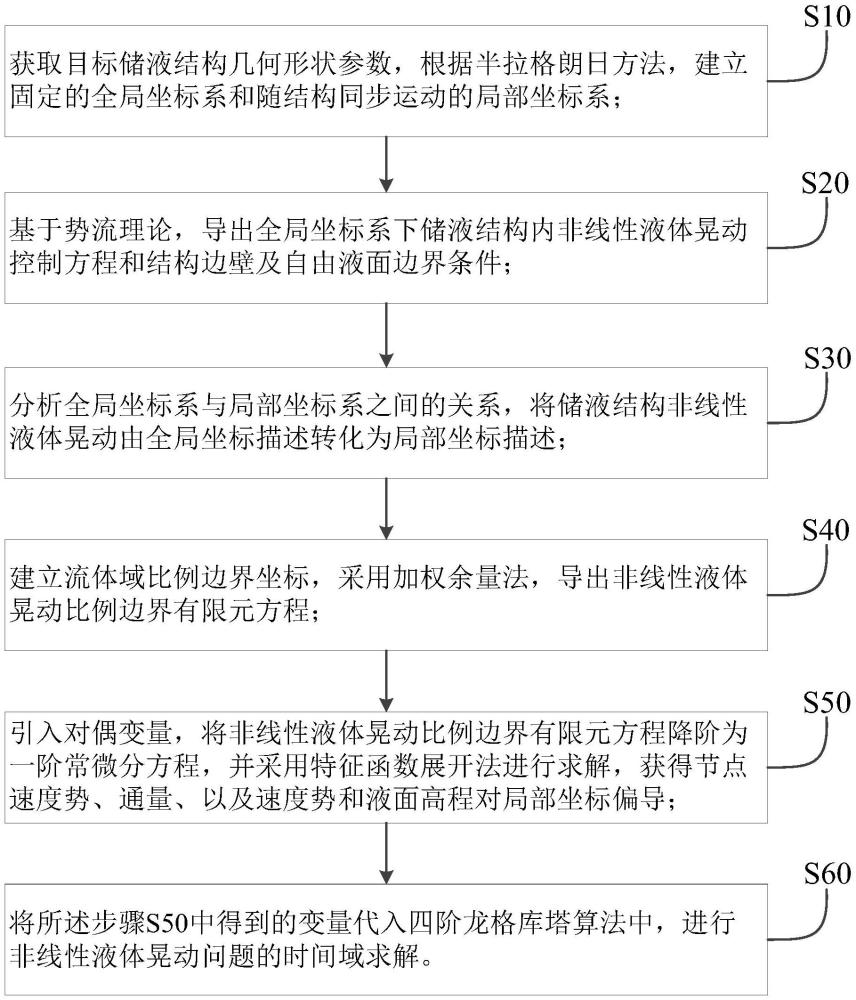
4、s10、获取目标储液结构几何形状参数，根据半拉格朗日方法，建立固定的全局坐标系和随结构同步运动的局部坐标系；

5、s20、基于势流理论，导出全局坐标系下储液结构内非线性液体晃动控制方程和结构边壁及自由液面边界条件；

6、s30、分析全局坐标系与局部坐标系之间的关系，将储液结构非线性液体晃动由全局坐标描述转化为局部坐标描述；

7、s40、建立流体域比例边界坐标，采用加权余量法，导出非线性液体晃动比例边界有限元方程；

8、s50、引入对偶变量，将非线性液体晃动比例边界有限元方程降阶为一阶常微分方程，并采用特征函数展开法进行求解，获得节点速度势、通量、以及速度势和液面高程对局部坐标偏导；

9、s60、将所述步骤s50中得到的变量代入四阶龙格库塔算法中，进行非线性液体晃动问题的时间域求解。

10、进一步的，所述步骤s10中，将整个水体所形成的流体区域定义为ω，根据半拉格朗日方法，建立全局固定笛卡尔坐标系oxz和随储液结构移动的局部坐标系oxz，初始时刻，两个坐标系源点均位于储液结构自由液面中心处，在结构晃动过程中，全局坐标系oxz位置保持不变，而局部坐标系oxz跟随储液结构同步运动。

11、进一步的，所述步骤s20中，假设流体无黏、无旋、不可压缩，根据势流理论，流体域ω内流场满足二维拉普拉斯方程：

12、

13、其中，为液体的速度势，为作用于x和z坐标的laplace算子，储液结构边壁和底部假设为刚性边界γrigid，边界条件需满足：

14、

15、其中，梯度算子sc＝(sx,sz)t，表示外荷载作用下储液结构的位移，n表示计算域边界单位外法线向量，自由液面上的运动学和动力学边界条件可表示为：

16、

17、其中，ηx表示液面高程，t为时间，g为重力加速度。

18、进一步的，所述步骤s30中，坐标系oxz与oxz之间满足下列关系：

19、

20、自由液面上的运动学和动力学边界条件可进一步表示为：

21、

22、其中，自由液面高程为η＝ηx-sz，自由液面上的速度势表示为：

23、

24、结合得到：

25、

26、同时，总速度势包括液体晃动和结构移动，即

27、

28、其中，φ为由液体晃动引起的速度势，后两项依次表示由结构沿横向和纵向移动对速度势的贡献。

29、局部坐标系xyz下的控制方程和边界条件表示为：

30、

31、其中，φ为由液体晃动引起的速度势，拉普拉斯算子和均是关于移动坐标系xyz的。

32、进一步的，所述步骤s40中，采用加权余量法，结合所述步骤s30中控制方程和边界条件可得如下弱形式积分方程：

33、

34、其中，vn表示oxz坐标系下流体速度，w是任意权函数；

35、定义径向和环向坐标分别为ξ和s，其中ξ取值区间为0至1，分别对应比例中心和域边界，沿环向将计算域几何边界离散为边界单元，采用局部坐标s∈[-1,1]用于高斯积分的程序实现；

36、关于坐标x和z的偏微分算子表示为：

37、

38、其中，|jb|＝xbzb,s-zbxb,s，

39、在比例边界坐标中，液体速度表示为：

40、

41、其中，[b1(s)]＝[b1(s)][n(s)]，[b2(s)]＝[b2(s)][n(s)],s，[n(s)]为与环向坐标相关的形函数矩阵；

42、采用伽辽金方法和格林函数理论，非线性液体晃动问题控制方程的积分弱形式最终解耦为如下表达式：

43、[e0]ξ2{φ(ξ)},ξξ+ξ([e0]+[e1]t-[e1]){φ(ξ)},ξ-[e2]{φ(ξ)}＝0

44、[e0]ξ{φ(ξ)},ξ+[e1]t{φ(ξ)}＝-∫s[n(s)]tvndγ,ξ＝ξ0

45、[e0]ξ{φ(ξ)},ξ+[e1]t{φ(ξ)}＝∫s[n(s)]tvndγ,ξ＝ξ1

46、上式即为非线性液体晃动问题比例边界有限元方程及其边界条件，其中

47、[e0]＝∫s[b1(s)]t[b1(s)]|jb|ds，

48、[e1]＝∫s[b2(s)]t[b1(s)]|jb|ds，

49、[e2]＝∫s[b2(s)]t[b2(s)]|jb|ds。

50、进一步的，所述步骤s50中，引入关于径向坐标ξ的对偶变量：

51、

52、其中，{q(ξ)}＝[e0]ξ{φ(ξ)},ξ+[e1]t{φ(ξ)}为流体通量，{q(ξ)}对ξ的偏导为：

53、{q(ξ)},ξ＝[e0]ξ{φ(ξ)},ξξ+[e0]{φ(ξ)},ξ+[e1]t{φ(ξ)},ξ

54、对所述步骤s40中非线性液体晃动比例边界有限元方程重新整理得到：

55、[e1]ξ{φ(ξ)},ξ+[e2]{φ(ξ)}＝[e0]ξ2{φ(ξ)},ξξ+[e0]ξ{φ(ξ)},ξ+ξ[e1]t{φ(ξ)},ξ

56、结合得到：

57、ξ{q(ξ)},ξ＝[e1]ξ{φ(ξ)},ξ+[e2]{φ(ξ)}

58、从流体通量表达式得到{φ(ξ)}对ξ的偏导数：

59、ξ{φ(ξ)},ξ＝[e0]-1{q(ξ)}-[e0]-1[e1]t{φ(ξ)}

60、考虑对偶变量{x(ξ)}，以上两式变为

61、ξ{x(ξ)},ξ＝[z]{x(ξ)}

62、其中，为hamiltonian矩阵；

63、非线性液体晃动一阶常微分方程解表示为下式：

64、{x(ξ)}＝ξλ{φ}

65、其中，λ和{φ}分别为[z]矩阵的特征值和特征向量。

66、进一步的，定义包含t时刻自由液面坐标和速度势的单一变量：

67、kt＝{xt,zt,φt}t

68、其中xt＝{x1,x2,x3,…,xnx}t，zt＝{z1,z2,z3,…,znx}t，φt＝{φ1,φ2,φ3,…,φnx}t；

69、其中，(xi)i＝1,2,…,nx、(zi)i＝1,2,…,nx和(φi)i＝1,2,…,nx表示自由液面第i个节点坐标和速度势，nx为沿x向节点总数，kt关于时间t的导数表示为：

70、

71、t+△t时刻自由液面节点坐标和速度势表示为：

72、

73、其中：

74、k1＝△tf(t,kt)

75、k2＝△tf(t+△t/2,kt+k1/2)

76、k3＝△tf(t+△t/2,kt+k2/2)

77、k4＝△tf(t+△t,kt+k3)。

78、进一步的，执行所述步骤s10至步骤s50得到t时间步所有边界节点速度势和通量，并将计算得到的t时刻所有边界节点速度势和通量代入所述步骤s60中，执行所述步骤s10至步骤s50得到t+△t时刻所有未知变量。

79、第二方面，本发明还提供了一种计算机可读存储介质，所述存储介质存储有计算机程序，所述计算机程序被处理器执行时实现如上所述方法。

80、第三方面，本发明还提供了一种电子终端，包括：处理器及存储器；所述存储器用于存储计算机程序，所述处理器用于执行所述存储器存储的计算机程序，以使所述终端执行如上所述方法。

81、本发明提供的非线性液体晃动的半解析数值仿真方法、介质及终端与现有技术相比，至少具有如下有益效果：

82、现有技术对液体晃动研究通常采用westergaard模型和housner弹簧-质量模型，存在精度和效率偏低的问题，另外现有数值仿真方法需要域内离散，网格更新繁琐，计算成本高。本发明采用比例边界有限元法模拟储液结构内流体非线性晃动问题，仅需离散计算域边界，沿径向具有解析性质，降低了计算维度，提高了计算效率；本发明基于势流理论、加权余量法和格林函数将储液结构内非线性液体晃动问题转化为求解二阶常微分方程，通过引入对偶变量将二阶常微分方程转化为一阶常微分方程，并采用特征向量展开法进行求解，同时采用四阶龙格-库塔算法进行时间域求解，提高了计算精度；本发明考虑了自由液面非线性边界条件，采用半拉格朗日方法定义全局坐标系和随储液结构同步运动的局部坐标系，网格更新只需在局部坐标系下自由表面进行，整个发明计算精度与效率高的同时，还降低了计算成本。