一种岩体高温-时效-弹塑性耦合损伤计算方法

本发明属于深部岩体工程，具体涉及一种岩体高温-时效-弹塑性耦合损伤计算方法。

背景技术：

1、随着深部矿产资源开采，地热资源采集和高地温隧道开挖等深部工程的发展，高温成为了制约安全生产不可忽略的重要因素。岩体本身具有强烈的非均质性，其内部不同矿物组分的热膨胀系数不同，会导致岩体在高温作用下产生温度应力。温度应力驱使岩体内部的孔隙和微裂纹不断发育、扩展、聚集成核，产生细观损伤，进而造成岩体宏观力学性质的劣化。此外，由于深部高地应力的作用，围岩在承受小于其抗压强度的荷载时，依然会产生蠕变变形，诱发迟滞性岩爆灾害。

技术实现思路

1、本发明为了解决现有技术中的不足之处，提供一种岩体高温-时效-弹塑性耦合损伤计算方法，本发明通过建立合理的本构模型，综合考虑高温和时效作用下岩体损伤的演化规律，对深部岩体工程的稳定性评价和防灾设计具有重要的工程实践意义。

2、为解决上述技术问题，本发明采用如下技术方案：一种岩体高温-时效-弹塑性耦合损伤计算方法，包括以下步骤：

3、s1、基于连续损伤力学、岩体粘弹塑性理论建立基于morh-coulomb(mc)准则的岩体时效-弹塑性耦合损伤模型；

4、s2、推导高温-时效-弹塑性耦合损伤演化方程，建立岩体高温-时效-弹塑性耦合损伤模型；

5、s3、针对岩石的非均质性，建立弹性模量和粘聚力的weibull分布方程；

6、s4、基于有限元方法和应力回映算法实现岩体高温-时效-弹塑性耦合损伤模型的数值求解；

7、s5、通过布谷鸟-有限元算法的迭代求解，获取岩体高温-时效-弹塑性耦合损伤模型的工程计算参数。

8、进一步的，步骤s1具体计算过程为：

9、s1-1、推导岩体时效损伤演化方程，具体过程如下：

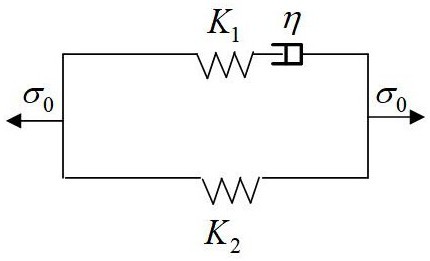
10、对岩体而言，当轴压小于长期强度时，岩体力学模型采用poytin-thomson模型进行表达，岩体本构方程为：

11、

12、式(1)中，ε为轴向应变；σ0为轴向应力；k1、k2、η均为弹性元件和黏性元件的力学参数；

13、对式(1)进行化简可得：

14、ε＝σ0[p+qexp(-rt)]   (2)

15、式中，

16、通过式(2)推导出弹性模量随时间的演化方程为：

17、e(t)＝p+qexp(-rt)   (3)

18、根据连续损伤力学理论，材料的时效损伤表示为：

19、

20、式(4)中，d(t)为时间效应引起的损伤变量；e为损伤后t时刻的弹性模量；e0为损伤前的弹性模量；

21、s1-2、建立岩体弹塑性损伤演化方程，具体过程如下：

22、当轴压大于长期强度时，岩体内部会出现弹塑性损伤dm，弹塑性损伤dm为变量，dm表示为的幂指数形式：

23、

24、式(5)中，α取值范围为(0,+∞)，决定了损伤后岩体材料软化曲线的初始斜率；β取值范围为[0,1)，决定了岩体最大损伤值；为等效塑性应变，表达式为：

25、

26、式(6)中，εp1、εp2、εp3分别为三个方向上的主塑性应变；

27、s1-3、推导时效-弹塑性耦合损伤演化方程，将岩石视为由未损伤、弹塑性损伤dm和时效损伤d(t)三部分组成；设未损伤、弹塑性损伤dm和时效损伤d(t)的作用面积分别为a1、am和at，总作用面积为a，当轴压低于长期强度时，岩体内部只发生时效损伤；根据连续损伤理论可知岩体时效损伤变量d(t)的表达式为：

28、

29、当轴压大于长期强度时，岩体内部未产生损伤的部分会发生塑性流动，产生弹塑性损伤dm；弹塑性损伤dm的表达式为：

30、

31、对整个岩石微元体而言，其总的耦合损伤dc是由时效损伤d(t)和弹塑性损伤dm共同组成；因此，耦合损伤dc的表达式为：

32、

33、将式(7)、(8)代入式(9)可得：

34、dc＝dr+dm-drdm   (10)

35、式(10)即为岩体时效-弹塑性耦合损伤表达式；

36、s1-4、基于mc准则建立考虑损伤的岩体时效-弹塑性耦合损伤模型，具体包括：考虑损伤作用的mc屈服准则表达式为：

37、

38、式中：i1为应力张量第一不变量；j2为应力偏量第二不变量；θ为罗德角；为内摩擦角；c为粘聚力；

39、其在主应力空间多屈服面形式为：

40、

41、由kuhn-tucker加卸载准则可得：

42、dλi≥0，fi≤0,，dλi，fi(σ，γ，dc)≤0   (13)

43、考虑损伤的应力-应变本构关系为：

44、

45、式中，εe为弹性应变；为损伤弹性矩阵，is为四阶对称张量，(is)ijkl＝1/2(vikδjl+δilδjk)；g(dc)、k(dc)分别为损伤剪切模量和体积模量；

46、g(dc)、k(dc)分别用初始剪切模量g0和初始体积模量k0表示：

47、

48、由式(15)看出，损伤最终还会导致岩体弹性模量发生弱化；

49、屈服势函数ψi与屈服函数形式相同，用膨胀角ψ代替内摩擦角即可；

50、当应力点在屈服函数面上时，只有一个塑性因子不为零：

51、

52、式(17)中：εp为塑性应变；γ为塑性因子；na为与塑性势函数ψ1正交的流动向量；

53、当应力点位于右棱线上，有两个塑性因子不为零：

54、

55、式(19)中：n6为与塑性势函数ψ6正交的流动向量；

56、当应力点位于左棱线上，塑性应变表达式与式(18)相同，此时:

57、

58、式(20)中：n2为与ψ2正交的流动向量；

59、当应力点位于mc准则的尖点处，6个塑性因子均不为零：

60、

61、累积塑性应变求解公式：

62、

63、进一步的，步骤s2具体过程为：

64、s2-1、高温造成的岩体损伤dt的演化方程为：

65、

66、式(23)中：et为高温影响后的弹性模量，其表达式为：

67、et＝a-bexp(c×t)   (24)

68、式(24)中：a、b、c均为常数，由试验拟合而得；t为温度；

69、s2-2、根据s1-3的推导过程，可得岩体高温-时效-弹塑性耦合损伤dco表达式为：

70、dco＝d(t)+dm+dt-d(t)dm-dtdm-dtdt+d(t)dmdt   (25)

71、将式(25)中的dco代替式(11)～(15)中的dc，可得岩体高温-时效-弹塑性损伤模型。

72、进一步的，步骤s3具体过程为：

73、将岩体视为有限多个代表性体积元(representative volume element，rve)的集合，则第i个rve单元中的某个力学参数可用weibull统计分布函数描述为

74、pi＝p0·xi   (26)式(26)中，p0为岩石试样的宏观性质，此处为弹性模量e和粘聚力c；xi为相应的weibull随机数；

75、x的累积分布函数(cumulative distribution function,cdf)w(x)和概率密度函数(probability density function,pdf)w(x)由双参数weibull分布演化为双参数weibull分布，此时的cdf和pdf的数学期望值和方差分别为：

76、

77、式中，г为gamma函数；e(x)为数学期望函数；var(x)为方差函数。

78、进一步的，步骤s4的具体过程为：

79、s4-1、给定计算时间，由式(23)和式(24)计算得到时效损伤值dt；如图6所示；

80、利用有限元方法计算tn+1荷载步的温度场，获得各高斯点上的温度值t，根据式(23)和式(24)获得温度dt的损伤值；

81、对于各向同性材料，温度只会引起膨胀或收缩，因此由式(31)计算tn+1时刻的温度应变：

82、

83、s4-2、有限元法中的已知量为tn时刻的应力增量σn，总应变εn+1和总应变增量δε；根据式(32)计算可得荷载应变增量：

84、δεepd＝δε-δεt   (32)

85、s4-3、根据弹性关系计算应力增量：

86、δσe＝deδε   (33)

87、式(33)中，δσe弹性应力增量；de为弹性本构矩阵；

88、此时，预测弹性应力可以表示为：

89、σtrial＝σn+δσe   (34)

90、式(34)中，σtrial为预测应力；

91、由于问题的对称性，在π平面上六分之一区域进行讨论；将预测应力各分量按照大小进行排序代入屈服函数(12)中的第一式进行判断，如果屈服函数：

92、

93、则当前计算步仍在弹性区，对所有变量进行更新：

94、

95、如果式(35)不成立，则需进行塑性修正，将试算应力映射回屈服面上。

96、进一步的，所述塑性修正的具体过程为：

97、假设更新应力位于屈服函数主平面上，则由式(16)可知，需对塑性因子增量δγ进行求解，假设初值：

98、

99、为tn+1时刻的等效塑性应变，为tn时刻的等效塑性应变；

100、此时相应的屈服函数为：

101、

102、建立new-raphson迭代式对δγ进行求解：

103、

104、进行收敛性判断：

105、

106、

107、式(41)中：

108、当|f1|≤tol时，计算完成，更新应力状态：

109、

110、对更新后的应力进行判定，如果σ1≥σ2≥σ3，则应力更新成立，对应力、应变和损伤变量进行更新，退出当前迭代步；否则假设返回应力位于棱线上；

111、在m-c准则的任意棱线上有偏应力si＝sj，其偏应力更新方程为：

112、

113、式(43)中：为na、nb的偏量部分；令t为垂直于的偏张量，则t为：

114、t1＝1-sinv，t2＝-2，t3＝1+sinψ   (44)

115、令:

116、

117、当s>0时，更新应力应在右棱线上，s<0时，更新应力在左棱线；

118、当返回应力位于右棱线时，根据塑性流动法则式(18)和式(19)，对δγa和δγb进行求解；

119、设定迭代计算初始值：

120、

121、在右棱线处应满足屈服方程f1＝0，f6＝0，即:

122、

123、式(47)中：

124、

125、建立δγa和δγb的newton-raphson迭代式子：

126、

127、式(51)中：d为残差矩阵，表达式如下：

128、

129、式(52)中：

130、

131、进行收敛性判断：

132、

133、当满足|f1|+|f6|＜0时，退出迭代过程，将求得δγa和δγb代入下面表达式进行更新：

134、

135、当返回左棱线时，将式(49)和式(54)进行重写，其他表达式不变：

136、

137、此时的应力更新表达式如下：

138、

139、对更新后的应力重新进行判断，如果满足σ1≥σ2≥σ3，返回右(左)棱线成立，否则返回尖点；

140、m-c屈服准则的顶点在静力水准轴上，其值为应力回映公式为：

141、

142、此时有pn+1＝p，即：

143、

144、又由可知，式(62)为的函数，利用newton-raphson法对进行求解：

145、设置迭代初始值：

146、

147、由式(62)建立残差方程：

148、

149、建立关于的迭代式：

150、

151、计算残差，进行收敛性检验：

152、

153、如果r≤tol，则计算收敛，对应力进行更新：

154、σ1：＝σ2：＝σ3：＝pn+1   (67)

155、应力计算完成后对弹塑性损伤dm进行更新，其表达式为：

156、

157、在新求得的损伤变量基础上，对应力进行再次修正：

158、

159、式(70)中：σ'n+1为最终计算所得的应力。

160、进一步的，步骤s5具体过程为：

161、s5-1、岩体高温-时效-弹塑性耦合损伤模型中的弹性模量e、泊松比μ、粘聚力c、内摩擦角ψ、温度损伤参数a、b和c，时效损伤参数p、q和r能够通过室内单、三轴压缩试验和蠕变试验确定，但是弹塑性损伤α和β采用峰后段曲线确定，且易受围压影响，需要依据工程实况进行反演；

162、根据工程设计图纸，建立有限元求解模型；由现场位移监测点的位置确定有限元模型中的研究节点；

163、s5-2、给定式(5)中损伤参数α和β的取值范围，其中α取值范围为[0,+∞]，β取值范围为[0,1]；

164、s5-3、初始化一个具有n个鸟窝的种群，被鸟巢主人发现的概率pa和迭代次数t，随机生成鸟巢的位置，每个鸟巢位置代表一对损伤参数(α，β)。

165、进一步的，步骤s5-3具体过程为：

166、1)、将每个鸟巢代表的损伤参数写入模型的有限元程序，计算研究节点的位移值，并与实测值带式(71)计算得到适应值，并保留具有最优适应值的鸟巢：

167、

168、式(71)中，fi为适应值；yi为监测点实际监测值；为有限元计算对应节点的位移值；n为预测样本个数；

169、2)、按照levy飞行过程进行鸟巢的更新：

170、

171、式(72)中，x(t+1)，xi(t)为鸟巢在第t+1次、第t次迭代时的位置；α为步长比例因子，α＞0；s为步长；为点对点乘法；l(s,λ)为随机游走的路径，并服从u＝t-λ的指数分布，其中λ为常数，一般取λ∈(1,3]；

172、levy飞行机制的核心是短距离游走和长距离跳跃交替变化，当处于短距离游走时种群的多样性将会提高，处于长距离跳跃时种群搜索具有方向的多样性，搜索更为详细；对称l(s,λ)稳定分布的积分形式为：

173、

174、式(73)没有解析解，当s≥s0＞0时，即：s→∞时，l(s,λ)的计算公式为：

175、

176、式(74)中，通常取β＝1；levy的飞行时间与方程呈指数关系，σ2(t)～t3-β，1≤β≤3；根据mantegna方法可以获得服从莱维分布的随机步长的方法，其表达式如下：

177、

178、3)、对更新后的鸟巢的适应度进行计算，与上代鸟巢的适应度进行比较并更新最优鸟巢的位置，判断是否满足条件，如果满足则停止迭代，否则返回第1)步。

179、采用上述技术方案，本发明相对现有技术具有突出的实质性特点和显著的进步，具体地说，本发明提供了一种适用于岩体的高温-时效-弹塑性耦合损伤模型，该模型能够表征温度、时间效应和荷载作用下的耦合损伤对岩体强度和刚度的弱化作用；提供的有限元算法和应力回映算法能够实现对模型精确、高效的求解；提供的布谷鸟-有限元耦合算法能够对模型中的损伤参数进行识别，提高模型的工程应用精度。