面向条件分支约束的智能车轨迹规划问题建模系统的制作方法

本发明涉及智能车轨迹规划问题建模，尤其涉及一种面向条件分支约束的智能车轨迹规划问题建模系统。

背景技术：

1、智能车的轨迹规划旨在生成反映行车局部路径与速度的时空轨线，使得车辆能够从给定的起始运动状态(一般包括车辆位置、姿态、行驶速度、加速度、前轮角度以及前轮角速度等)迁移至既定的终止运动状态，符合车辆内部运动学约束与外部环境避障约束等，并在严格保障上述约束得以满足的前提下尽量使得既定的性能指标(一般从行车安全隐患、轨迹平滑性、乘车舒适性等方面考虑)得到优化。

2、轨迹规划问题的顺利求解依赖精准高效的轨迹规划问题模型构建，即轨迹规划问题建模技术，本方法聚焦于轨迹规划问题求解之前的问题建模环节，拟提出一种实现高性能问题建模的信息化系统。

3、车辆在行驶过程中，往往会遭遇一些条件分支约束，它们书写为“如果xxx-那么xxx”的格式，例如，如果车辆驶入某一局部既定区域，那么车速应不高于10km/h。这些条件分支约束呈现不可微分的性质，如果在轨迹规划命题的构建环节掺入这种条件分支约束，则所构建的命题难以被有效求解。

4、目前市面上不存在能够在轨迹规划任务遭遇条件分支约束时妥善解决轨迹规划问题模型可微分性的建模技术。因此，有必要提出一种面向条件分支约束的智能车轨迹规划问题建模系统，以解决上述问题。

技术实现思路

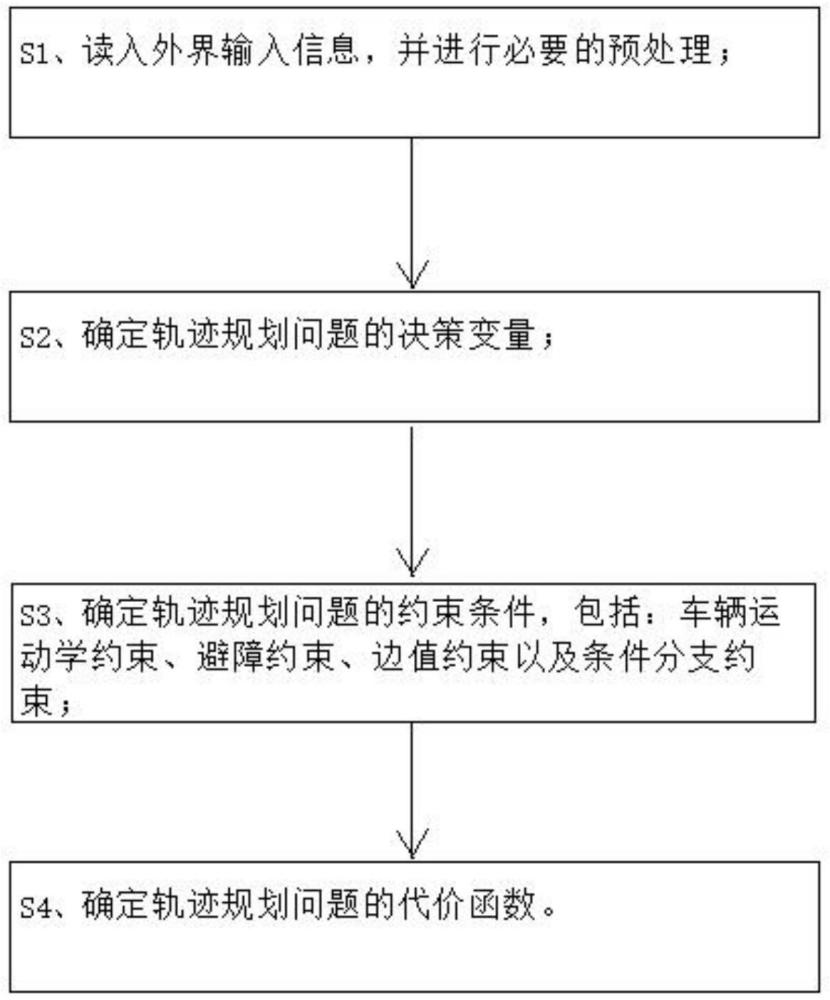
1、本发明针对在轨迹规划命题的构建环节掺入不可微分性质的条件分支约束时，则所构建的命题难以被有效求解的问题，提出了一种面向条件分支约束的智能车轨迹规划问题建模系统，包括以下处理步骤：

2、s1、输入端信息的读入与预处理；

3、s2、确定轨迹规划问题的决策变量；

4、s3、确定轨迹规划问题的约束条件，所述约束条件包括：车辆运动学约束、避障约束、边值约束以及条件分支约束；其中前三项都是寻常轨迹规划问题中的约束，而最后一项，即条件分支约束是本专利最核心的原创的技术；其中所述条件分支约束原理为：

5、最简单的条件分支约束，即

6、if q≥0,then g(q)≥0,        (4)

7、其中q为函数的自变量；

8、已知sigmod函数σ(q)的表达式为：

9、

10、其中自变量q∈(-∞,+∞)，n＞0为充分大的正实数，n取值越大则σ(q)对阶跃函数step(q)的拟合效果越好；

11、利用sigmoid函数σ(q)将条件分支约束式(4)书写为以下处处光滑可微分的不等式约束：

12、(σ(q)-ε2)·g(q)≥-ε，      (6)

13、其中ε→0+为充分小的正实数参数，以下针对式(6)的合理性进行解释与分析：

14、当q＞0时，σ(q)→1，不等式(6)退化为(1-ε2)·g(q)≥-ε，即

15、

16、由于ε与0的距离充分小，-ε/(1-ε2)→0-，此时不等式(7)可近似表征约束g(q)≥0，拟合误差为-ε/(1-ε2)；

17、当q＜0时，σ(q)-ε2→-ε2。此时不等式(6)简化为-ε2·g(q)≥-ε，即g(q)≤ε-1。由于ε→0+，所以ε-1→+∞，因此g(q)≤ε-1等价于g(q)≤+∞，这表示(6)在q＜0条件下并未对g(q)取值产生限制，因此符合条件分支约束式(4)表示的内容；

18、当q＝0时，σ(0)＝0.5，此时不等式(6)表示为(0.5-ε2)·g(0)≥-ε，即g(0)≥-ε/(0.5-ε2)；由于ε→0+，-ε/(0.5-ε2)→0-，所以不等式(6)可在临界条件q＝0之处近似表征g(q)≥0，拟合误差为-ε/(0.5-ε2)；

19、综上所述，式(6)能够在一定误差容限内将条件分支约束(4)近似地表示；

20、在式(4)基础上，更一般的条件分支约束可记为以下格式：

21、if f(q)≥0,then g(q)≥0，        (8)

22、其中q为函数的自变量；类比于式(6)，此时的处处可微分表达式可构建为：

23、(σ(f(q))-ε2)·g(q)≥-ε，       (9)

24、因此，“如果…那么…”语句所表示的基本语句可以利用式(9)予以表达；

25、然而，有时语句是复合型的，例如具有“如果a(q)<0且b(q)<0，那么c(q)<0或d(q)<0或e(q)<0”这样的更为复杂的语句；为此，逻辑表达式之中的或、与的建模方法，以及在条件分支约束中掺入或、与表达式后构成的复合条件分支表达式的建模方法为：

26、首先，针对“与”运算进行建模，采用以下“与”运算约束

27、(f1(q)≤0)∧(f2(q)≤0)，         (10)

28、该式等价于：

29、max(f1(q),f2(q))≤0，          (11)

30、由于max()运算可以由logsumexp函数估计，因此式子(11)可表示为以下处处可微分的光滑表达式：

31、

32、在上式中，n＞0，n为由用户设置的影响拟合精度的常数，n越大则拟合max()运算的精度越高；

33、其次，对“或”运算进行建模，采用以下“或”运算表达式：

34、(f1(q)≤0)∨(f2(q)≤0)        (13)

35、该式等价于：

36、min(f1(q),f2(q))≤0，        (14)

37、将其转化为针对max()的运算，即：

38、max(-f1(q),-f2(q))≥0，       (15)

39、在上述或、与表达式的基础上，一则复合条件分支约束表达式则为：

40、“如果a(q)<0且b(q)<0，那么c(q)<0或d(q)<0或e(q)<0”

41、首先，将“如果”语句部分表达出来，其内容为“a(q)<0且b(q)<0”，基于上述推导，该表达式应书写为：

42、

43、即：

44、

45、其次，将“那么”语句部分表达出来，其内容为“c(q)<0或d(q)<0或e(q)<0”，基于上述推导，该表达式应书写为：

46、

47、在分别处理完“如果”、“那么”语句后，完整的条件分支约束表达式，此时套用公式(9)，将式(18)视为f(q)、将式(19)视为g(q)，则有

48、

49、综上所述，式(20)以处处光滑的方式表示了“如果a(q)<0且b(q)<0，那么c(q)<0或d(q)<0或e(q)<0”这样的复合条件分支约束；

50、所以，条件分支约束的建模方法具体为以下步骤：

51、step1，明确列出条件分支约束语句，形如“如果a(q)<0且b(q)<0，那么c(q)<0或d(q)<0或e(q)<0”；

52、step2，从上述语句中提取出“如果”表达式，如以上式为例，“如果”表达式为a(q)<0且b(q)<0；随后利用或、与表达式转化公式(12)或(16)对其进行处处可微分化表示，表示结果为一个代数不等式，记为m(q)>0；

53、step3，从上述语句中提取出“那么”表达式，如以上式为例，“那么”表达式为c(q)<0或d(q)<0或e(q)<0；随后利用或、与表达式转化公式(12)或(16)对其进行处处可微分化表示，表示结果为一个代数不等式，不妨记为p(q)>0；

54、step4，利用式(9)表示“如果m(q)>0，那么p(q)>0”，并将所构建的处处可微分的约束记录下来；

55、s4、确定轨迹规划问题的代价函数；

56、将上述步骤中构造的决策变量、约束、代价函数合在一起，就构成了一则完整的轨迹规划问题数据，随后将其输出系统，以便下游使用。

57、在本发明的一个优选实施方式中，s1中输入端信息的读入与预处理具体包括：

58、首先，从系统外部读入车辆当前状态信息，即车辆当前客观上的运动状态，此时加速度为a0，速度为v0，姿态角度为theta0，前轮角度为phi0，前轮角速度为omega0，车辆后轮中心点的横坐标位置为x0，纵坐标位置为y0，将上述变量存储下来，准备后续步骤之中使用；

59、其次，从系统外部读入车辆轨迹规划任务信息，具体包括车辆行驶的局部终点运动状态，假设轨迹规划的时间区间是t∈[0,t]，其中t>0，t代表局部轨迹规划的完成时刻，是由用户指定的已知参数，例如t＝10秒；在t时刻，假设任务指定的加速度为af，速度为vf，姿态角度为thetaf，前轮角度为phif，前轮角速度为omegaf，车辆后轮中心点的横坐标位置为xf，纵坐标位置为yf。将上述变量存储下来，准备后续步骤之中使用；

60、接着，读入高精度地图，并将其中记录的、位于(x0,y0)附近且可能影响到行车过程的固定障碍物，记录在集合set_obs之中，其中每个元素elem是一个结构体变量，代表每一个障碍物的轮廓信息，假设每个障碍物在惯性坐标系中占据的区域是一个凸多边形(凹多边形可拆解为一系列凸多边形)，elem结构体利用其x与y字段记录了该多边形的有序顶点坐标；

61、最后，读入传感器识别到的地面标识信息，并将其表示为条件分支语句，例如“如果车辆后轮中心点落在某个地面凸多边形区域内，那么车速不应超过10km/h”，或者“如果车辆后轮中心点落在某个地面凸多边形区域内且车辆姿态角度在某一区间内，那么车速不应低于5km/h或车辆前轮转角不应超过0.5rad”；记录在一个字符串str之中存储下来，准备后续步骤之中使用。

62、进一步地，s2中确定轨迹规划问题的决策变量包括：x(t)代表t时刻车辆后轮中心点所在位置在惯性坐标系中的横坐标值，y(t)代表t时刻车辆后轮中心点所在位置在惯性坐标系中的纵坐标值，v(t)及a(t)分别代表车辆在t时刻的速度与加速度，φ(t)代表在t时刻的车辆的前轮偏转角，ω(t)为t时刻的前轮偏转角速度，θ(t)代表车辆在t时刻的姿态角；上述所有变量中t∈[0,t]。

63、进一步地，s3中车辆运动学约束为：

64、

65、其中lw代表车辆轮轴距。

66、进一步地，s3中避障约束为：

67、环境中的障碍物记录在集合set_obs之中，假设其中每个凸多边形障碍物elem占据的二维平面空间表示为occupied(elem)，那么避障约束条件则表示为：

68、(2)

69、其中fp(·,·,·):代表从位置姿态到车身在二维平面投影的非线性映射，公式(2)表示在0～t时间内的任意一个时刻t，车身与任意一个静态障碍物均不发生碰撞。

70、进一步地，s3中边值约束为：

71、在初始时刻t＝0以及终止时刻t＝t，车辆按照行驶任务会处于相应的运动状态，相关数值已传递至系统中，因此两点边值约束构建为以下等式：

72、

73、进一步地，s4中确定轨迹规划问题的代价函数的具体方法为：

74、轨迹规划问题的代价函数应确保车辆行驶平顺，则将代价函数设计为：

75、

76、其中，wa,ww＞0为权重；

77、代价函数体现了自动驾驶车辆因变化速度或变化前轮角度而消耗的能量，该项越小则车辆行驶轨迹越平顺，通过调节权重wa,ww即可在行车轨迹的速度平顺性与方向平顺性上做出折中与权衡。

78、实施本发明实施例，具有如下有益效果：

79、本面向条件分支约束的智能车轨迹规划问题建模系统首次系统性地解决了条件分支约束的处处光滑(处处可微分)建模难题，不仅具有理论高度，在实际工程实践中具有非常好的实践效果；

80、经过矿山自动驾驶营运车辆长达600余天的实际使用数据统计，该方法使得条件分支约束的建模覆盖率持续保持在100％，且从未失败，因此具有很好的算法(系统)稳定性。