一种求解大变形曲梁支反力的计算方法

本发明涉及曲梁支反力分析，特别涉及一种求解大变形曲梁支反力的计算方法。

背景技术：

1、曲梁在大变形时其刚度特性会产生明显的非线性变化，通过改变曲梁的形状，可以实现所需要的刚度特性。因此，曲梁常常被作为准零刚度隔振装置的准零刚度元件，如图3所示，其通常被认为是一端固定，一端可动铰支。由于曲梁的特殊刚度特性是由曲梁发生大变形屈服产生的，而传统的梁理论是在小线性假设下提出的，在大变形情况下，其中性轴形状不满足经典梁理论的假设，因此传统的梁理论不再适用于大变形曲梁的分析。

2、目前，针对大变形曲梁的分析问题，主要的计算方法是非线性有限元方法和打靶法。非线性有限元方法在分析大变形曲梁问题上具有较高的可信度，但是其计算过程较长，且存在几何更改复杂、与计算软件(matlab和python等)进行交互时间长的问题。而在设计所需要的准零刚度元件时，需要对大量的曲线形状进行分析，然后迭代寻优，这会导致优化过程存在迭代效率低的问题。打靶法在已知外力求解曲梁的变形时，通过合理设置求解容差，其求解效率和精度均较高。典型准零刚度的力-位移曲线如图4所示，在准零刚度区间时，其支反力差别很小，这意味着对于给定力的准零刚度元件求解，打靶法在准零刚度区间求解得到的位移值有无限多个。而对于给定位移的情况，在允许容差范围内，其支反力可以认为具有唯一性。但是，这种情况需要进行反复迭代求解，计算效率较低。

3、针对给定位移的情况下，打靶法计算大变形曲梁的支反力需要进行反复迭代求解的问题，现有技术尚未进行研究和解决，大变形曲梁支反力的计算效率较低。

技术实现思路

1、本发明提供了一种求解大变形曲梁支反力的计算方法，用以解决现有技术中大变形曲梁支反力的计算效率较低的问题。

2、一方面，本发明提供了一种求解大变形曲梁支反力的计算方法，包括以下步骤：

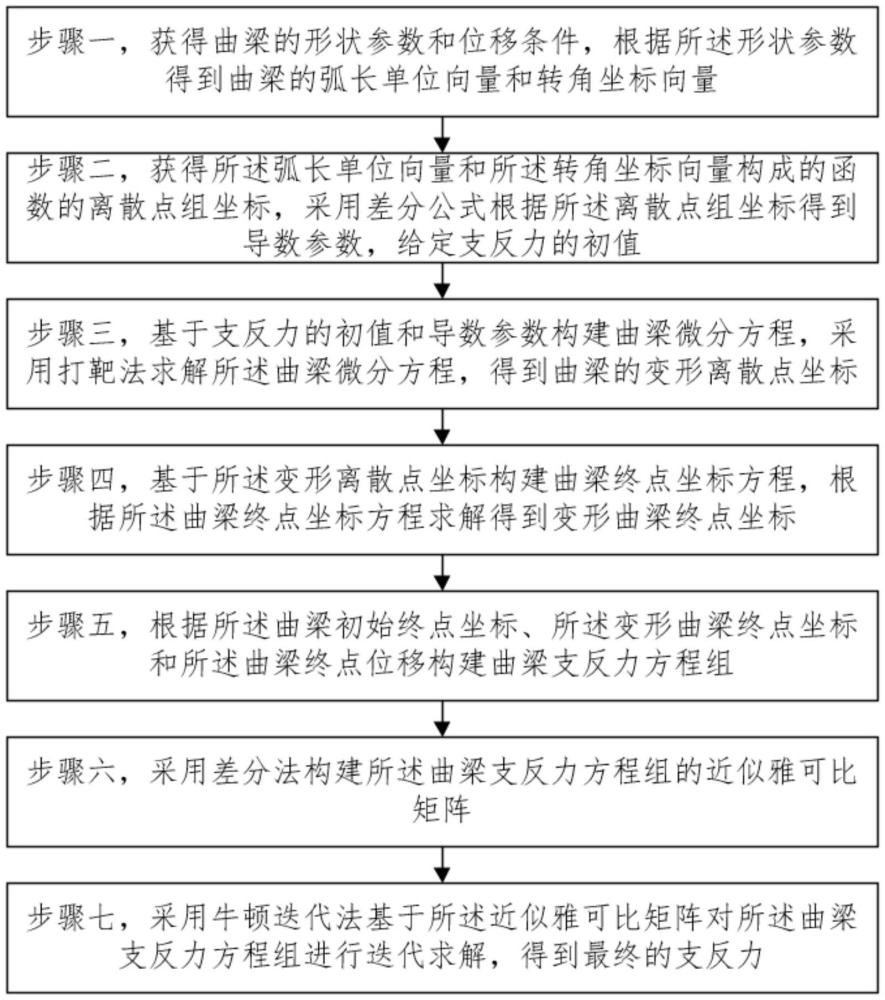
3、步骤一，获得曲梁的形状参数和位移条件，根据所述形状参数得到曲梁的弧长单位向量和转角坐标向量。

4、所述形状参数包括：曲梁起点坐标、曲梁初始终点坐标和曲梁离散点坐标，所述位移条件包括：曲梁终点位移。

5、步骤二，获得所述弧长单位向量和所述转角坐标向量构成的函数的离散点组坐标，采用差分公式根据所述离散点组坐标得到导数参数，给定支反力的初值。

6、步骤三，基于支反力的初值和导数参数构建曲梁微分方程，采用打靶法求解所述曲梁微分方程，得到曲梁的变形离散点坐标；所述支反力包括：竖向外载荷和横向外载荷。

7、步骤四，基于所述变形离散点坐标构建曲梁终点坐标方程，根据所述曲梁终点坐标方程求解得到变形曲梁终点坐标。

8、步骤五，根据所述曲梁初始终点坐标、所述变形曲梁终点坐标和所述曲梁终点位移构建曲梁支反力方程组。

9、步骤六，采用差分法构建所述曲梁支反力方程组的近似雅可比矩阵。

10、步骤七，采用牛顿迭代法基于所述近似雅可比矩阵对所述曲梁支反力方程组进行迭代求解，得到最终的支反力。

11、在一种可能的实现方式中，步骤一中，根据弧长公式得到曲梁的弧长向量和总弧长，所述弧长单位向量是根据所述弧长向量和所述总弧长得到。

12、所述转角坐标向量是根据转角坐标公式得到。

13、在一种可能的实现方式中，步骤七包括：

14、设置迭代条件。

15、当所述迭代条件不满足时，采用牛顿迭代公式对所述竖向外载荷和所述横向外载荷进行更新，并返回步骤三进行迭代。

16、当所述迭代条件满足时，输出当前迭代的支反力的初值，即为最终的支反力。

17、本发明中的一种求解大变形曲梁支反力的计算方法，具有以下优点：

18、通过结合打靶法求解曲梁微分方程、差分法构建曲梁支反力方程组的近似雅可比矩阵、牛顿迭代法对曲梁支反力方程组进行迭代求解，在保证计算精度的前提下提高了曲梁支反力的计算效率。

技术特征：

1.一种求解大变形曲梁支反力的计算方法，其特征在于，包括以下步骤：

2.根据权利要求1所述的一种求解大变形曲梁支反力的计算方法，其特征在于，步骤一中，根据弧长公式得到曲梁的弧长向量和总弧长，所述弧长单位向量是根据所述弧长向量和所述总弧长得到；

3.根据权利要求2所述的一种求解大变形曲梁支反力的计算方法，其特征在于，步骤一中，所述弧长公式如下式所示：

4.根据权利要求1所述的一种求解大变形曲梁支反力的计算方法，其特征在于，步骤二中，获得所述弧长单位向量u和所述转角坐标向量η构成的函数η(u)的离散点组坐标(u,η)，采用差分公式根据所述离散点组坐标(u,η)得到导数参数，包括：d2η/du2、η(0)和η(1)；

5.根据权利要求4所述的一种求解大变形曲梁支反力的计算方法，其特征在于，步骤三中，基于支反力的初值和导数参数构建曲梁微分方程如下式所示：

6.根据权利要求5所述的一种求解大变形曲梁支反力的计算方法，其特征在于，步骤四中，所述曲梁终点坐标方程如下式所示：

7.根据权利要求6所述的一种求解大变形曲梁支反力的计算方法，其特征在于，步骤五中，所述曲梁支反力方程组如下式所示：

8.根据权利要求7所述的一种求解大变形曲梁支反力的计算方法，其特征在于，步骤六中，所述近似雅可比矩阵j如下式所示：

9.根据权利要求1所述的一种求解大变形曲梁支反力的计算方法，其特征在于，步骤七包括：

技术总结本发明公开了一种求解大变形曲梁支反力的计算方法，包括以下步骤：获得曲梁的形状参数和位移条件，根据形状参数得到曲梁的弧长单位向量和转角坐标向量；构建曲梁微分方程，采用打靶法求解曲梁微分方程，得到曲梁的变形离散点坐标；构建曲梁终点坐标方程，根据曲梁终点坐标方程求解得到变形曲梁终点坐标；构建曲梁支反力方程组；采用差分法构建曲梁支反力方程组的近似雅可比矩阵；采用牛顿迭代法对曲梁支反力方程组进行迭代求解，得到最终的支反力。本申请通过结合打靶法求解曲梁微分方程、差分法构建曲梁支反力方程组的近似雅可比矩阵、牛顿迭代法对曲梁支反力方程组进行迭代求解，在保证计算精度的前提下提高了曲梁支反力的计算效率。技术研发人员：刘静,李鑫斌,许亚军,刘建昱,潘光受保护的技术使用者：西北工业大学技术研发日：技术公布日：2024/9/9