一种非均质地聚物再生混凝土细观数值模型建模方法

本发明属于混凝土细观数值计算，尤其涉及一种非均质地聚物再生混凝土细观数值模型建模方法。

背景技术：

1、地聚物再生粗骨料混凝土作为一种典型的非均质复合材料，主要由天然粗骨料、再生粗骨料、河砂、胶凝体、孔隙等组成。这些组分在空间中随机分布，使得不同材料单元表现出不同的物理力学性质，试件内部表现出显著的非均匀性，进一步影响了地聚物再生混凝土宏观力学性能，使其呈现出显著的离散性。此外粉煤灰颗粒形状、大小和碱激发剂模数均会影响地聚物反应进程、反应速率及最终反应产物，造成了地聚物砂浆基底力学性能上的差异性。添加的再生粗骨料由于存在更多的内部缺陷进一步加剧了地聚物再生粗骨料混凝土的不均匀性，从而导致其抗压强度表现出更大的随机性和离散性。《混凝土强度检验评定标准》(gb/t 50107-2010)中所选用的混凝土离散程度值，主要是基于过去混凝土种类相对有限的情况，对普通混凝土进行统计分析后得出的结果。然而，随着混凝土种类的日益丰富，尤其是绿色建筑材料地聚物再生混凝土的出现，其强度离散程度明显偏大，原规定对地聚物再生混凝土的离散程度存在不适用性。因此有必要在现有规范的基础上，对地聚物再生混凝土进行深入的研究，并根据实际情况做出适当的调整，以确保评定标准的准确性和适用性。在进行地聚物再生粗骨料混凝土细观数值研究时，其通常被认为是由粗骨料、粗骨料-旧砂浆界面过渡区、旧砂浆、旧砂浆-新砂浆界面过渡区和新砂浆组成，各相均质的材料。但是，材料细观结构构成及其性质会显著影响宏观尺度上的力学性能及对数值计算结果的离散性统计分析，采用均质细观模型会忽略材料单元的差异性，影响数值计算的精度。然而各相划分网格后单元数量通常具有数十万个甚至百万个，通过试验或以往研究数据获取各个单元参数是有困难的。因此地聚物再生混凝土细观数值研究急需一种将细观结构与单元材料属性相关联，提高计算精度，进而描述细观结构对grac宏观力学离散性能的影响。

技术实现思路

1、为解决上述技术问题，本发明提出了一种非均质地聚物再生混凝土细观数值模型建模方法，实现了对地聚物再生粗骨料混凝土宏观力学性能离散性的有效模拟。

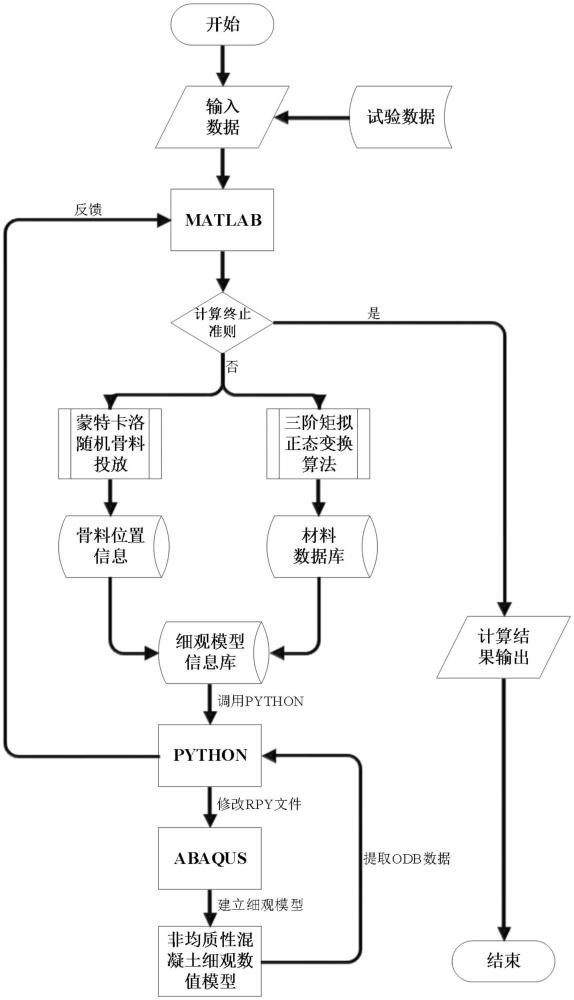
2、为实现上述目的，本发明提供了一种非均质地聚物再生混凝土细观数值模型建模方法，包括：

3、s1、获取地聚物再生混凝土力学试验数据；

4、s2、根据预设的试件尺寸信息结合所述地聚物再生混凝土力学试验数据，通过蒙特卡洛算法计算骨料大小、数量及位置信息；

5、s3、在matlab中搭建互相关变量三阶矩拟正态变换算法框架，确定互相关变量及拓展后材料数量，结合骨料大小、数量及位置信息，构建非均质细观模型信息库，为步骤s4计算材料本构模型时提供材料抗压强度、弹性模量、峰值应变参数数值；

6、s4、在python中基于《混凝土结构设计规范》和混凝土弹塑性损伤模型，提取s3建立的非均质细观模型信息库中各材料的抗压强度、弹性模量、峰值应变数值，建立所述地聚物再生混凝土细观成分的塑性本构模型参数计算程序；

7、s5、编写abaqus有限元模型py程序，提取s2计算骨料信息和s4材料本构模型数据，构建地聚物再生混凝土非均质细观模型；

8、s6、调用abaqus运行s5编写py程序，基于所述地聚物再生混凝土非均质细观模型进行计算，获得计算结果；

9、s7、通过matlab调用python调取abaqus计算结果，存储到matlab中，并对所述计算结果进行统计；若满足终止条件则计算终止，获得数值结果用于表征地聚物再生混凝土宏观强度离散性能，若不满足终止条件则返回s2，重复步骤s2至s7。

10、进一步的，所述互相关变量包括抗压强度、弹性模量和峰值应变。

11、进一步的，搭建互相关变量三阶矩拟正态变换算法框架，确定互相关变量及拓展后材料数量，结合骨料大小、数量及位置信息，构建非均质细观模型信息库的方法为：

12、x为基于选定的随机变量的有限试验数据，所述有限试验数据指砂浆抗压强度、弹性模量、峰值应变，其中含有n组数据，xi为其中的第i组数据，分别为抗压强度xic，弹性模量xie和峰值应变xic；描述相关随机变量之间关系的为公式(3)，[xic xie xiε]是互相关随机变量，[zic zie ziε]是互相关标准正态随机变量，u是独立标准正态变量；

13、x＝[x1 x2 … xi … xn]t (1)

14、xi＝[xic xie xiε]t (2)

15、

16、其中，μc,μe和με，σc,σe和σε是基于试验数据，各指定随机变量的均值和标准差；zic、zie和ziε是正态标准空间内互相关变量，ac/ae/aε、bc/be/bε及cc/ce/cε组成系数矩阵；

17、依据测量数据的偏度信息求解[θc θe θε]t，

18、

19、其中，和基于试验数据，统计后得到的各指定随机变量的偏度；

20、获取[θc θe θε]t值后，ac/ae/aε、和cc/ce/cε下式求解，

21、

22、cc/ce/cε,bc/be/bεc求解完成后得到公式(5)；

23、根据相关系数的定义，互相关变量xic、xie和xiε之间的相关系数为ρce、ρeε和ρεc，对试验数据统计分析得到，见公式(6)；

24、互相关标准正态变量zic、zie和ziε之间的相关系数为ρ0ce、ρ0eε和ρ0εc，相关系数矩阵在式(7)；正态空间互相关变量相关系数之间的关系ρ0ce、ρ0eε和ρ0εc通过式(8)和ρce、ρeε和ρεc之间的关系求解获得；

25、

26、对cz进行cholesky分解，将cz分为下三角矩阵和其转置的乘积，如式(9)，uij为独立标准正态随机向量ui中第j个元素，ui和zi之间的关系如式(10)；

27、

28、将式(10)和式(11)带入到式(3)得到式(12)，得到互相关随机向量xi由独立标准正态随机向量ui表示，完成独立标准正态随机变量的逆正态变换；

29、

30、利用matlab生成m个独立标准正态随机向量ui，并将ui带入式(12)后建立新材料库wnew；为保证材料库材料单元属性的合理性，材料强度、弹性模量和峰值应变需要满足式(15)，确保材料单元发生了塑性损伤变形；

31、u＝[u1 u2 … ui … um]t (13)

32、wnew＝[x1 x2 … xi … xn]t (14)

33、

34、进一步的，根据《混凝土结构设计规范》和混凝土弹塑性损伤模型，计算所述地聚物再生混凝土力学试验数据的材料损伤因子和应力-应变关系的方法包括：

35、

36、其中，σc和σt分别是单轴抗压和和抗拉强度；dc和dt分别代表混凝土在单轴压缩和拉伸下的损伤因子；e0是初始弹性模量；εc和εt分别是单轴压缩和拉伸应变；和分别是单轴塑性压缩和拉伸应变。

37、本发明技术效果：本发明公开了一种非均质地聚物再生混凝土细观数值模型建模方法，解决了传统均质细观模型无法精确表征单元材料在空间上的异质性和随机性的问题，从而实现了对地聚物再生粗骨料混凝土宏观力学性能离散性的有效模拟；本发明在地聚物再生混凝土细观数值计算领域提出的基于非正态互相关变量三阶矩拟正态变换算法的地聚物再生混凝土细观非均质建模方法相对于传统的均质细观模型具有显著的计算精度优势，构建了一个全面且完整的数值分析框架，能够精确地模拟地聚物再生混凝土的概率破坏行为，为地聚物再生混凝土的性能分析和优化提供了有力支持。