一种基于页岩气压裂井下裂缝实时三维拟合系统及方法

本发明涉及页岩气开发，具体涉及一种基于页岩气压裂井下裂缝实时三维拟合系统及方法。

背景技术：

1、在页岩气开发这一前沿领域，水力压裂技术是解锁深层页岩中天然气资源的关键。然而，面对地下地质构造的复杂性和天然裂缝网络的不确定性，当前的压裂过程实时拟合技术暴露出显著的局限性，这不仅影响了开采效率，也限制了对地下资源的准确评估和有效开发。

2、具体而言，现有技术存在的问题主要包括：模型简化与现实脱节：传统压裂模拟技术往往忽视了地下地质结构的复杂性，尤其是天然裂缝的分布、走向及其对压裂效果的直接影响。这种简化处理导致模型与实际地层特性之间存在较大差距，模拟结果难以准确反映真实压裂过程，降低了开采策略的针对性和有效性。

3、在考虑地质复杂性时，模型计算量急剧增加，现有的计算方法和硬件设施往往难以在保证精度的同时，实现高效的数据处理和分析。这导致实时性要求高的压裂过程控制与优化成为难题，影响现场决策的时机。

4、基于此，急需一种基于页岩气压裂井下裂缝实时三维拟合系统及方法，能够在实现对井下裂缝实时准确的三维拟合的同时确保拟合的高效率。

技术实现思路

1、本发明的目的之一在于提供一种基于页岩气压裂井下裂缝实时三维拟合系统及方法，能够在实现对井下裂缝实时准确的三维拟合的同时确保拟合的高效率。

2、为了达到上述目的，提供了一种基于页岩气压裂井下裂缝实时三维拟合系统，包括：

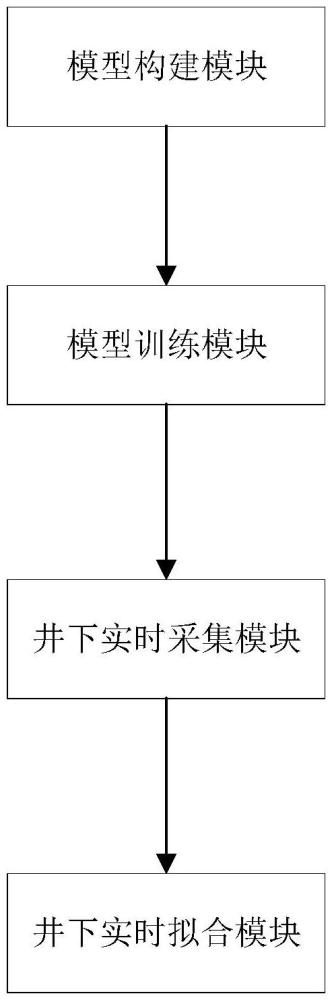
3、模型构建模块，用于通过简化的三维位移不连续法，构建数值模拟模型；所述简化的三维位移不连续法仅在缝高方向离散一个单元；

4、模型训练模块，用于从数据库中获取历史真实地层所对应的历史地质参数、历史压裂曲线以及历史微地震数据，并将历史地质参数作为数值模拟模型的输入，输出对应的预测压裂曲线和预测裂缝形态，并通过历史微地震数据，构建历史裂缝形态，并基于预测压裂曲线和预测裂缝形态，以及历史压裂曲线和历史裂缝形态，通过预设的模型训练策略，对数值模拟模型进行迭代训练，直到满足最大迭代次数；

5、井下实时采集模块，用于实时获取当前真实地层所对应的当前地质参数；

6、井下实时拟合模块，用于将当前地质参数作为训练好后的数值模拟模型的输入，输出对应的当前压裂曲线和当前裂缝形态。

7、本方案的技术原理及效果：在本方案中首先通过简化的三维位移不连续法来实现对应的数值模拟模型的构建，且该简化的三维位移不连续法仅在缝高方向离散一个单元，相比三维位移不连续方法，通过排除非垂直裂缝和剪应力垂直分量的微小简化以及消除了垂直高度方向上的离散化，在保证裂缝形态模拟的精度的同时裂缝模拟的计算效率也得到提高了。

8、之后通过数据库中的历史真实地层的历史地质参数、历史压裂曲线以及历史微地震数据，其中，将历史地质参数输入到数值模拟模型中，输出预测压裂曲线和预测裂缝形态，通过历史为地质数据来构建历史裂缝形态，之后通过预测压裂曲线和预测裂缝形态，以及历史压裂曲线和历史裂缝形态，采用预设的模型训练策略，来对数值模拟模型进行迭代训练，直到满足最大迭代次数，从而实现了对数值模拟模型的训练和优化，极大提高了智能拟合的可靠性和准确性。

9、之后实时采集当前真实地层的当前地质参数，输入到训练完成后的数字模拟模型中去，从而实现对当前真实地层的实时三维拟合，输出对应的当前压裂曲线和当前裂缝形态。

10、1、数值模拟模型的构建采用的简化的三维位移不连续法，该简化的三维位移不连续法不仅可以计算单条裂缝的位移不连续量和诱导应力，而且可以计算三维多条裂缝的位移不连续量和诱导应力。与现有的三维位移不连续方法相比，通过排除非垂直裂缝和剪应力垂直分量(沿x2方向)的微小简化，以及消除垂直(高度)方向上的离散化，计算效率提高了一千多倍，极大提高了模拟天然裂缝等复杂缝网的模拟准确性和可靠性。

11、2、通过预测压裂曲线和预测裂缝形态，以及历史压裂曲线和历史裂缝形态，实现对构建好的数值模拟模型的迭代训练，进而提高数值模拟模型在后续的实时三维拟合的过程中的可靠性，极大程度的降低了手工调参时间，提高了实时三维拟合的拟合效率。

12、进一步，所述模型训练模块包括：

13、历史数据获取输入模块，用于从数据库中获取历史真实地层所对应的历史地质参数、历史压裂曲线以及历史微地震数据，并将历史地质参数作为数值模拟模型的输入；

14、初始化模型参数模块，用于对jaya算法和数值模拟模型进行参数初始化，所述jaya算法设计种群大小为20，算法终止条件为达到最大迭代次数100，算法设计变量为2；所述数值模拟模型中正则化参数μ和核函数参数σ经过多次试验，优化取值范围分别为[0.1，100]和[0.1，500]；

15、目标函数定义模块，用于对数值模拟模型所对应的目标函数计算公式进行定义；

16、所述目标函数计算公式为：

17、

18、式中，mse为数值模拟模型对预测压裂曲线与历史压裂曲线的均方误差，为预测压裂曲线中第i个点所对应的预测值，yi为历史压裂曲线中第i个点所对应的真实值；n为压裂曲线所对应的总点数；

19、随机分配模块，用于在正则化参数μ和核函数参数σ的取值范围内随机生成一组向量[γ，δ]，为jaya算法的种群内每一个个体分配一组(γ，δ)；

20、目标函数计算模块，用于根据数值模拟模型训练结果，基于目标函数计算公式，计算出当前种群的最优解xj，best,i和最差解xj，worst,i，所述最优解xj，best,i为mse最大的解，最差解xj，worst,i为mse最小的解；

21、修正模块，用于根据计算出来的当前种群的最优解xj，best,i和最差解xj，worst,i，修正迭代过程中目标函数的当前解，形成修正后的解；

22、所述修正的解的计算逻辑为：

23、x′j，k,i＝xj，k,i+r1j，i(xj，best,i-|xj，k,i|)-r2j，i(xj，worst,i-|xj，k,i|)

24、式中，x′j，k，i为修正后的解，xj，k，i为当前解；

25、判断模块，用于判断修正后的解x′j,k,i是否优于当前解xj，k，i，若是，则保留修正后的解，否则保留当前解，将所有保存的解作为下一次迭代的输入；

26、循环输出模块，用于判断当前迭代次数是否达到最大迭代此时，若否，则继续迭代，继续计算种群的最优解和最差解，反之则输出最优解xj,best,i，并输出对应最优的参数组合(γ,δ)。

27、有益效果：在本方案通过以目标函数值作为实际响应，结合jaya对算法参数进行最优化训练，速收敛于模型参数的最优解，大幅度减少算法和反演研究的计算时间，提高反演精度，同时通过最优参数组合的输出，实现对数值模拟模型的优化，为后续的裂缝形态预测和压裂曲线预测提供了更为可靠的模型。

28、进一步，所述通过历史微地震数据，构建历史裂缝形态包括以下步骤：

29、对采集到的历史微地震数据进行数据预处理，所述数据预处理包括噪声过滤操作、误报剔除操作以及时间校正；

30、根据各个历史微地震数据所对应的到达时间差，确定每一个微地震数据所对应的三维空间坐标；

31、对确定三维空间坐标的微地震数据进行空间聚类分析，基于微地震数据之间的空间分布密度，对微地震数据进行分组，每一个组为对应的潜在裂缝段；

32、对每一个聚类分组内的微地震数据进行拟合，拟合出代表裂缝面的平面或者曲面模型，并计算出裂缝的产状参数，所述产状参数包括裂缝走向、裂缝倾向和裂缝倾角；

33、根据拟合出来的平面或者曲面模型，以及计算出来的裂缝的产状参数，构建单个裂缝的三维几何形态，并整合形成完整的离散裂缝网络模型，将该离散裂缝网络模型作为对应的历史裂缝形态。

34、有益效果：在本方案中通过精确识别和分析裂缝网络分布、延伸方向和连通性，可以更准确的评估压裂作业的结果，提高压裂效果评估精度。

35、进一步，所述地质参数包括天然裂缝倾角、天然裂缝长度和天然裂缝数量，以及其他地质工程参数，其中天然裂缝倾角、天然裂缝长度和天然裂缝数量为变量，其他地质工程参数为常量。

36、有益效果：在本方案中，天然裂缝倾角、天然裂缝长度和天然裂缝数量为变量，可以准确的模拟出不同地址条件下的裂缝网络的复杂结果和分布模式，有助于理解裂缝系统的空间分布特征，且准确的模拟出天然裂缝的特征对于制定有效的压裂策略尤为关键，极大提高了后续压裂策略的可靠性。

37、本发明还提供一种基于页岩气压裂井下裂缝实时三维拟合方法，使用上述的基于页岩气的井下裂缝实时三维拟合系统，包括以下步骤：

38、s1、通过简化的三维位移不连续法，构建数值模拟模型；所述简化的三维位移不连续法仅在缝高方向离散一个单元；

39、s2、从数据库中获取历史真实地层所对应的历史地质参数、历史压裂曲线以及历史微地震数据，并将历史地质参数作为数值模拟模型的输入，输出对应的预测压裂曲线和预测裂缝形态，并通过历史微地震数据，构建历史裂缝形态，并基于预测压裂曲线和预测裂缝形态，以及历史压裂曲线和历史裂缝形态，通过预设的模型训练策略，对数值模拟模型进行迭代训练，直到满足最大迭代次数；

40、s3、实时获取当前真实地层所对应的当前地质参数；

41、s4、将当前地质参数作为训练好后的数值模拟模型的输入，输出对应的当前压裂曲线和当前裂缝形态。