一种图像AIGC模型推断速度的优化方法与流程

本发明涉及人工智能，特别涉及一种图像aigc模型推断速度的优化方法。

背景技术：

1、近年来，随着深度学习和计算机视觉技术的迅猛发展，人工智能生成内容(aigc)技术在图像生成、图像修复、风格转换等方面取得了显著进展。aigc技术通过训练深度神经网络模型，可以从无到有生成高质量的图像，或对已有图像进行修复和优化。这些技术已经在许多领域中得到广泛应用，包括娱乐业、医疗影像、自动驾驶等。然而，尽管现有aigc技术在生成图像质量方面取得了显著成效，但其推断速度和处理效率仍存在较多问题，这限制了其在实时和大规模应用中的广泛推广。

2、目前，生成对抗网络(gan)和变分自动编码器(vae)是aigc领域最常用的技术。gan通过生成器和判别器的对抗训练，能够生成具有高度逼真性的图像；vae则通过概率模型的方式生成图像，在保持图像质量的同时具有一定的生成多样性。然而，这些技术在实际应用中面临如下问题：gan和vae模型通常包含大量的参数和层级结构，训练和推断过程需要大量的计算资源和时间。特别是在生成高分辨率图像时，计算复杂度显著增加，导致推断速度缓慢，难以满足实时应用的需求。gan在训练过程中容易出现模式崩溃(mode collapse)和梯度消失(vanishing gradient)等问题，导致生成图像的多样性不足和质量不稳定。vae在保持生成图像质量和多样性之间也存在权衡问题。现有的aigc模型在特征提取方面仍存在局限性。尽管卷积神经网络(cnn)在特征提取方面表现优越，但在处理复杂和多样性较高的图像时，现有模型提取的特征可能不够充分和准确，影响生成图像的质量。现有aigc技术在模型参数优化方面仍有待改进。传统的优化方法在应对大规模和高维度数据时，效率较低，难以快速适应动态变化的输入数据和生成需求。

技术实现思路

1、鉴于此，本发明提供了一种图像aigc模型推断速度的优化方法，显著提高了图像aigc模型的推断速度和生成质量。同时，基于质量评估结果的动态参数优化机制，使得模型具有高度的鲁棒性和适应性，能够在各种复杂应用场景中表现出色。

2、本发明采用的技术方案如下：

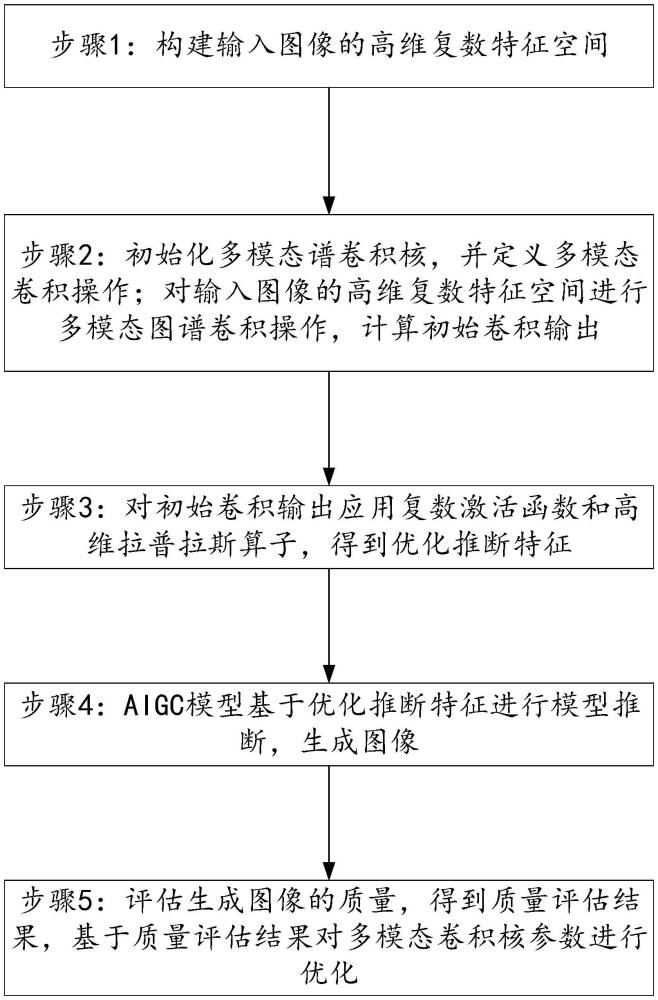
3、一种图像aigc模型推断速度的优化方法，所述方法包括：

4、步骤1：构建输入图像的高维复数特征空间；

5、步骤2：初始化多模态谱卷积核，并定义多模态卷积操作；对输入图像的高维复数特征空间进行多模态图谱卷积操作，计算初始卷积输出；

6、步骤3：对初始卷积输出应用复数激活函数和高维拉普拉斯算子，得到优化推断特征；

7、步骤4：aigc模型基于优化推断特征进行模型推断，生成图像；

8、步骤5：评估生成图像的质量，得到质量评估结果，基于质量评估结果对多模态卷积核参数进行优化。

9、进一步的，步骤1具体包括：计算输入图像的复数矩阵表示；使用复数域的多尺度分解，将复数矩阵映射到不同频率和特征维度上，同时引入分形维度参数对不同频率和特征维度进行扩展和加权，再通过复数高斯-勒让德变换进行平滑处理，得到输入图像的高维复数特征空间。

10、进一步的，使用如下公式，计算输入图像的复数特征表示：

11、

12、其中，im，n为输入图像i的复数矩阵表示；im，n为输入图像的二维矩阵表示；i为虚数单位，定义为i2＝-1；为对输入图像进行hilbert变换，得到其瞬时幅值和相位信息；m和n分别表示输入图像在水平方向和垂直方向上的像素坐标；通过如下公式，使用复数域的多尺度分解，将复数矩阵映射到不同频率和特征维度上，同时引入分形维度参数对不同频率和特征维度进行扩展和加权，得到复数分形表示fm，n，k：

13、

14、其中，fm，n，k表示第k个特征维度上的复数分形表示；p，q分别表示水平方向上和垂直方向上的的频率范围；fm和fn分别表示水平方向上和垂直方向上的频率成分；β为分形维数参数，用于调节多尺度分解中的权重；αk为分形维数参数，控制特征维度k的扩展程度；p和q均为下标索引。

15、进一步的，使用如下公式，复数分形表示fm，n，k通过复数高斯-勒让德变换进行平滑处理，得到输入图像的高维复数特征空间：

16、

17、其中，σ为高斯函数的标准差；m和n分别为输入图像在水平方向和垂直方向上的像素个数；pm，n(z)为勒让德多项式；z为高维复数变量。

18、进一步的，步骤2中的初始化的多模态谱卷积核使用如下公式进行表示：

19、

20、其中，wu，v，l表示在空间位置(u，v)和通道l上的多模态谱卷积核；ω0为初始频率参数。

21、进一步的，使用如下公式，对输入图像的高维复数特征空间进行多模态图谱卷积操作，计算初始卷积输出：

22、

23、其中，x(1)表示初始卷积输出；表示对所有特征提取路径进行求和，s表示特征提取路径的总数；s为下标索引；表示沿着特征提取路径γs进行积分运算；*表示卷积操作；gm表示多模态图谱的图结构；ξs(θ)为多模态特征提取函数，定义为：

24、

25、其中，θs为路径角度中心；θ为角度变量；σ2表示路径角度的尺度；r为时间域变换函数的数量；r为下标索引；φr(τ)为时间变换域函数，τ为时间变量；φr(τ)＝exp(-αrτ2)cos(βrτ)；其中，αr为时间衰减参数；βr为时间频率参数。

26、进一步的，步骤3中，通过如下公式，对初始卷积输出应用复数激活函数：

27、

28、其中，φ(x(1))表示复数激活函数。

29、进一步的，通过如下公式，对初始卷积输出应用复数激活函数后，再乘以高维拉普拉斯算子，得到优化推断特征。

30、进一步的，步骤5中，通过评估生成图像与预期生成图像的差别，得到质量评估结果，具体包括：计算生成图像与预期生成图像在对应位置的像素差值，得到所有位置的像素差值的总和后，除以像素总数，作为质量评估结果；多模态卷积核中的初始频率参数除以质量评估结果，完成优化。

31、采用以上技术方案，本发明产生了以下有益效果：本发明通过高维复数特征空间的构建，有效提升了图像特征的表示能力。复数特征表示不仅包含幅度信息，还引入了相位信息，使得特征表示更加丰富和全面。通过这种方式，可以在不增加计算复杂度的前提下，显著提高特征提取的效率，进而加快模型的推断速度。多模态谱卷积核的设计结合了高斯函数和平面波函数，使得卷积操作既能够捕捉局部特征，又能保持全局的相位信息和频率信息。高斯函数部分通过权重的合理分布，确保了卷积核在不同空间位置上的平滑过渡和噪声抑制，而复数平面波函数部分则通过方向性和频率选择性，增强了卷积核对复杂图像特征的响应能力。这种多模态谱卷积核的使用，大大提高了卷积操作的效率，从而加快了特征提取和处理的速度。复数激活函数通过对初始卷积输出进行非线性变换，增强了特征表示的复杂性和丰富性。高维拉普拉斯算子的引入，通过计算特征表示的二阶导数，突出特征中的局部变化，有效增强了特征中的边缘和细节信息。两者的结合，使得特征表示不仅具有更高的非线性和复杂性，还能更好地反映图像中的局部和全局信息，从而优化了推断过程，提高了整体计算效率。