可解释负荷时序高维拓扑特征提取方法及系统与流程

本发明属于电力负荷数据分析领域，涉及一种可解释负荷时序高维拓扑特征提取方法及系统。

背景技术：

1、随着电力系统现代化管理的发展，智能电网的能源规划和分配日益受到人们的重视。这有助于确保可持续性和避免资源浪费。负荷数据分析是智能电网的重要组成部分，越来越受到学术界的关注。负荷数据分析能够对电力需求做出智能和有效的响应，允许采取明智和有效的行动。准确的负荷数据分析可以缓解电力供需矛盾，支持电网可靠稳定运行。

2、传统的负荷数据分析方法可以分为统计方法和机器学习方法。近年来，随着深度学习的发展，深度学习也得到了广泛的应用。与统计方法和传统机器学习不同，深度学习不需要人工特征提取，端到端模型为负荷数据分析带来便利。然而，这些方法只是直接分析负荷数据，而没有提取负荷数据的特征。考虑到负荷数据的特点，单纯使用深度学习模型仍有局限性。电力负荷数据经常表现出周期性、非线性和非平稳性，因此从负荷数据中提取有意义的特征对提高精度具有重要意义。

3、对于短期负荷数据分析，虽然负荷数据显示每日、每周和每年的周期模式，但人们关注的是更精细的日内时间尺度建模。在日内时间尺度上，信号显示出显著和快速的波动。需要建立更精细的时间尺度模型，并沿着时间轴捕获波动性。这使得预测的未来负荷更尖锐和多样化，可以很好地适应实际情况。传统的提取方法存在精度不足或缺乏可解释性等问题。因此，如何提高负荷特征提取的精度和可解释性是亟待解决的问题。

技术实现思路

1、为了解决上述问题，本发明提出了一种可解释负荷时序高维拓扑特征提取方法及系统，该方法具有较强的可解释性，在降低计算成本的同时提高了精度。

2、为了解决上述技术问题，本发明采用的技术方案为：

3、第一方面，本发明提供一种可解释负荷时序高维拓扑特征提取方法，包括：

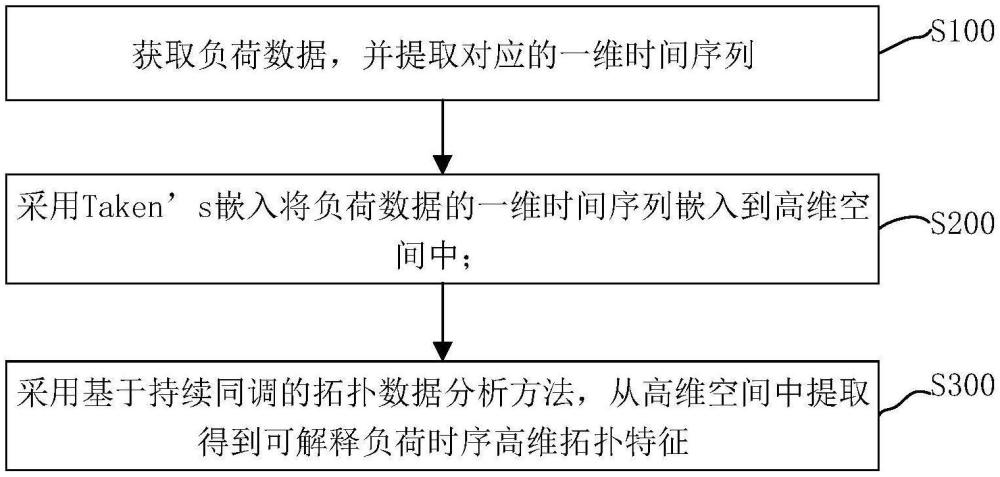
4、获取负荷数据，并提取对应的一维时间序列；

5、采用taken’s嵌入将负荷数据的一维时间序列嵌入到高维空间中；

6、采用基于持续同调的拓扑数据分析方法，从高维空间中提取得到可解释负荷时序高维拓扑特征。

7、作为本发明进一步改进，所述taken’s嵌入的嵌入过程包括选择合适的嵌入维度和时间延迟；嵌入维数是指用于表示重构相空间中每个点的坐标数，时间延迟决定了这些点之间的间距。

8、作为本发明进一步改进，所述taken’s嵌入的包括：

9、

10、其中是一个满秩的全映射，为一个n维的紧密流形；r×m→m和f:m→r为光滑函数；对于任意τ>0，映射m→r2n+1。

11、作为本发明进一步改进，所述采用基于持续同调的拓扑数据分析方法，从高维空间中提取得到可解释负荷时序高维拓扑特征，包括：

12、将有限度量空间s视为欧几里德空间的子集，将s∈视为具有固定半径∈的球的并集；计算s∈的单纯同调以得到其单纯复形的过程称为持续同调；

13、给定一组顶点v，单纯形就是v的集合；单纯形σ的维数是|σ|-1；单纯形σ是τ的一个面，如果则表示为一个单纯复形k被定义为一组单纯形k的维数是其单纯形的最大维数σ；图g＝(v，e)是顶点v和边集给定一个图，构造复形：

14、

15、使用同源性计算给定拓扑空间内特定维度的结构数，k中的d维单纯表示为σ1，…，σ维链是d维单纯形的和；

16、所有d维链的集合形成一个表示为cd(k)的向量空间；给定单纯形d的边界为：

17、

18、如果则α∈cd(k)的d链是一个循环；如果存在(d+1)-chainβ使得则是一个边界，边界表示为bd(k)，d维同调群为hd(k)＝zd(k)/bd(k)；

19、再进行过滤复形，过滤复形包含称为过滤值的附加参数，其中，每个单纯形都与一个过滤值或参数相关联，用实数表示；过滤是嵌套简单复形的集合为：

20、

21、给定一个过滤，得到关于同调的图谱序列为

22、hd(k1)→hd(k2)→…→ha(kn)

23、其中，每个ki都是一个简单的复数，ki是i≤j的ki的子集；

24、与每个单纯形相关的过滤值沿序列不递减，滤波后的复形通常使用持续性图或持续性条形码进行可视化，特征的持续性是特征存在或持续存在的过滤值范围，可视化后得到可解释负荷时序高维拓扑特征。

25、作为本发明进一步改进，所述基于持续同调的拓扑数据分析方法是：采用自适应持续同调对计算出的单纯复形进行统计分析，根据拓扑特征的统计分布自适应的选取阈值，具体包括：

26、利用持续同调中的vietoris-rips复形来构建，并将其持续性表示为条码；再采用统计方法对条码分布进行分析并选取阈值。

27、作为本发明进一步改进，所述利用持续同调中的vietoris-rips复形来构建，并将其持续性表示为条码，包括：

28、1)构建vietoris-rips复形

29、对于一个邻域图是(g，w)，其中g＝(v，e)是无向图，w：e→r是由其边定义的权函数；给定和尺度ε∈r，则vr邻域图为邻域图(gε(s)，w)，其中gε(s)＝(d，eε(s))，且

30、eε(s)＝{{u，v}| d(u，v)≤ε，u≠v∈s}

31、

32、通过vietoris-rips扩张计算vietoris-rips复形如果单纯形的所有边ε都在g中，则ε就在中；对于g＝(v，e)，有

33、

34、对于

35、

36、2)持续条码表示

37、对于计算出的vietoris-rips复形中的每个复形，其持续性被定义为从出现到消失的持续时间；对二维复合物的持续性进行统计分析；

38、拓扑特征的出现时间记为b，消失时间记为d，持续性计算公式为(b-d)；vietoris-rips复形的持续性用持续条码来描述；持续条码是一个二维图形，其中横轴表示特征的出现时间，纵轴表示特征的消失时间。

39、作为本发明进一步改进，所述采用统计方法对条码分布进行分析并选取阈值，包括：

40、根据持续条码的长度对其进行排序，并选择出现时间的第三四分位数作为过滤值。

41、第二方面，本发明提供一种可解释负荷时序高维拓扑特征提取系统，包括：

42、获取模块，用于获取负荷数据，并提取对应的一维时间序列；

43、嵌入模块，用于采用taken’s嵌入将负荷数据的一维时间序列嵌入到高维空间中；

44、提取模块，用于采用基于持续同调的拓扑数据分析方法，从高维空间中提取得到可解释负荷时序高维拓扑特征。

45、第三方面，本发明提供一种电子设备，包括存储器、处理器以及存储在所述存储器中并可在所述处理器上运行的计算机程序，所述处理器执行所述计算机程序时实现所述可解释负荷时序高维拓扑特征提取方法。

46、第四方面，本发明提供一种计算机可读存储介质，所述计算机可读存储介质存储有计算机程序，所述计算机程序被处理器执行时实现所述可解释负荷时序高维拓扑特征提取方法。

47、第五方面，本发明提供一种计算机程序产品，所述计算机程序产品包括计算机指令，所述计算机指令指示计算机执行所述可解释负荷时序高维拓扑特征提取方法。

48、第六方面，本发明提供一种基于可解释负荷时序高维拓扑特征的未来负荷预测方法，包括：

49、获得短期负荷数据；

50、采用所述可解释负荷时序高维拓扑特征提取方法对短期负荷数据进行处理，提取得到可解释负荷时序高维拓扑特征；

51、将可解释负荷时序高维拓扑特征与短期负荷数据的原始时间序列结合，输入到模型中，得到电力负荷的预测结果。

52、第七方面，本发明提供一种基于可解释负荷时序高维拓扑特征的未来负荷预测系统，包括：

53、获得模块，用于获得短期负荷数据；

54、处理模块，用于采用所述可解释负荷时序高维拓扑特征提取方法对短期负荷数据进行处理，提取得到可解释负荷时序高维拓扑特征；

55、预测模块，用于将可解释负荷时序高维拓扑特征与短期负荷数据的原始时间序列结合，输入到模型中，得到电力负荷的预测结果。

56、本发明相对于现有技术具备的有益效果为：

57、本发明提出了一种基于持续同调的高精度、低成本、可解释的拓扑特征提取方法，来解决短时负荷数据分析中的特征工程问题，采用taken’s嵌入将负荷的一维时间序列嵌入到高维空间中，在高维空间中能够捕获更为精细的时间序列波动，采用基于持续同调的拓扑数据分析方法，从高维空间中提取拓扑特征，并将其与原始时间序列相结合，作为模型的输入，提升了模型的精度。