基于特征临界值分析的模型无关精确可解释方法

本发明涉及可解释机器学习，具体涉及一种基于特征临界值分析的模型无关精确可解释方法。

背景技术：

1、以神经网络为基础的机器学习技术近年来在各个领域得到广泛应用并取得了优秀的成果，引领人工智能相关技术取得了长足的进步。尽管机器学习模型取得了巨大的成功，机器学习模型的弊端也逐渐显现：一方面，研究表明机器学习模型在对抗性扰动方面很脆弱，输入上的一点细微的扰动就会导致模型做出错误的决定。另一方面，由于其黑盒性质以及不透明的学习过程，人们很难理解其内部运行机理及决策依据，进而无法确认模型所给的输出结果是否可靠。以上问题直接影响到机器学习模型的应用推广及现实影响力。为提高人们对机器学习模型的信任度，增强人机协同，可解释机器学习应运而生。

2、可解释机器学习寻求对模型预测结果提供人类能理解的解释，以揭示模型的逻辑和行为机理，这不仅能增加用户对模型的信任和接受度，还有助于满足法规和伦理要求。可解释机器学习的基本标准是解释必须让人类能够理解决策模型如何得出预测结果，即特征对解释结果起积极或消极的作用，从而人类可以根据解释的结果选择是否相信模型的预测结果。这种解释结果的透明性不仅有助于故障排查和模型性能改进，还对于揭示和纠正模型中可能存在的偏见和不公平性具有重要意义，推动着人工智能在各个领域的可持续发展和应用。可解释机器学习的解释方法分为模型相关解释和模型无关解释，模型相关解释侧重于说明模型的总体决策逻辑，而模型无关解释则是侧重于说明模型对于某个实例的预测。其中，模型无关的可解释方法可以揭示机器学习模型给定输入与相应的输出信息之间的关联，通过展示实例重要特征对预测结果的影响或是揭示模型预测的判断依据，让人们了解模型是否根据正确的逻辑得出预测结果。然而，传统模型无关可解释方法需要对样本进行不加限制的随机扰动，这会生成与样本相差过大的、甚至是有违常理的扰动样本，且对所有扰动样本进行线性回归拟合无法精确原模型的决策边界。为此，传统模型无关可解释方法生成的解释结果存在不稳定且不够忠实于原模型的问题。

技术实现思路

1、本发明所要解决的是现有模型无关可解释方法生成的解释结果不稳定且不够忠实于原模型的问题，提供一种基于特征临界值分析的模型无关精确可解释方法。

2、为解决上述问题，本发明是通过以下技术方案实现的：

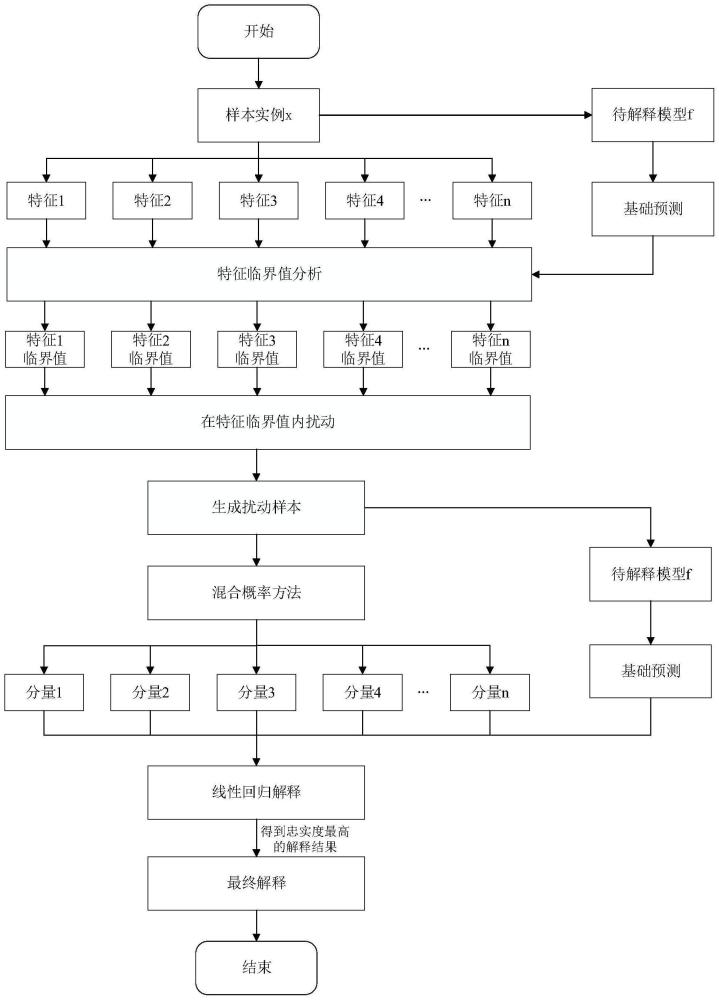
3、基于特征临界值分析的模型无关精确可解释方法，包括步骤如下：

4、步骤1、将待解释样本输入到待解释模型中，得到待解释模型的基线预测值；

5、步骤2、对待解释样本的一个特征进行扰动，通过在当前特征的最小取值和最大取值的范围内对当前特征的特征值进行逐步变化，得到基于当前特征的l个单扰动待解释样本；

6、步骤3、将基于当前特征的l个单扰动待解释样本分别输入到待解释模型中，得到待解释模型的基于当前特征的l个单扰动预测值；

7、步骤4、计算当前特征的敏感度：

8、

9、其中，si为当前特征的第i个敏感度，y′i为基于当前特征的第i个单扰动预测值，y为基线预测值，z′i为当前特征的第i个变化扰动特征值，z为当前特征的原始特征值，i＝1,2,…,l，l为基于当前特征的单扰动待解释样本的数量；

10、步骤5、基于当前特征的l个敏感度确定当前特征的临界值：即若存在当前特征的第i个变化扰动特征值z′i使当前特征的第i个敏感度si的导数为0时，基于当前特征的第i个单扰动预测值y′i不等于基线预测值y，则将当前特征的第i个变化扰动特征值z′i记为当前特征的临界值；否则，将当前特征的原始值作为当前特征的临界值；

11、步骤6、遍历待解释样本的所有特征，重复步骤2～5，得到待解释样本的各个特征的临界值；

12、步骤7、对待解释样本的所有特征进行扰动，通过对每个特征的特征值在其临界值的范围内进行随机变化，得到m个全扰动待解释样本；其中m为人为设定的正整数；

13、步骤8、通过混合概率方法对m个全扰动待解释样本进行分组，得到k个样本分组；其中k为人为设定的正整数；

14、步骤9、分别对每个样本分组中的全扰动待解释样本进行线性回归拟合，得到k个拟合解释模型；

15、步骤10、对于每个样本分组，将当前样本分组的每一个全扰动待解释样本分别输入到待解释模型和当前样本分组的拟合解释模型中，得到待解释预测值和拟合预测值，并据此计算当前样本分组的拟合解释模型和待解释模型的差异度：

16、

17、式中，φk表示当前样本分组的拟合解释模型gk和待解释模型f的差异度；x″j′表示样本分组k中的第j′个全扰动待解释样本，f(x″j′)表示样本分组k中的全扰动待解释样本x″j′的待解释预测值，gk(x″j′)表示样本分组k中的全扰动待解释样本x″j′的拟合预测值，j′＝1,2,…,mk，mk表示样本分组k中全扰动待解释样本的数量；

18、步骤11、将与待解释模型的差异度最小的样本分组的拟合解释模型作为最终的解释模型。

19、上述步骤2中，基于当前特征的单扰动待解释样本的数量l由当前特征的最小取值和最大取值确定的取值范围和变化步长所决定。

20、上述步骤7中，在对待解释样本的每个特征的特征值在其临界值的范围内进行随机变化时：若该特征的原始特征值介于该特征的最小取值和该特征的临界值之间，则该特征的随机扰动特征值介于该特征的最小取值和该特征的临界值之间；若该特征的原始特征值介于该特征的临界值和该特征的最大取值之间，则该特征的随机扰动特征值介于该特征的临界值和该特征的最大取值之间；若该特征的原始特征值等于临界值，则该特征的随机扰动特征值介于该特征的最小取值和该特征的最大取值之间。

21、上述步骤8的具体过程如下：

22、步骤8.1、设置样本分组的数量k，并初始化每个样本分组的权重、均值和协方差；

23、步骤8.2、遍历m个全扰动待解释样本，基于每个样本分组的权重、均值和协方差，计算当前全扰动待解释样本相对于每个样本分组的后验概率，并将当前全扰动待解释样本分类到后验概率最高的样本分组中；

24、步骤8.3、将m个全扰动待解释样本分类完成后，基于每个样本分组中的全扰动待解释样本及其后验概率，更新每个样本分组的权重、均值和协方差；

25、步骤8.4、重复步骤8.2和8.3，直至参数收敛即本次所得到的每个分组中的扰动待解释样本与上次所得到的每个分组中的扰动待解释样本均相同，此时m个全扰动待解释样本被分类到k个样本分组中。

26、上述步骤8.2中，全扰动待解释样本x″j相对于每个样本分组k的后验概率pjk为：

27、

28、式中，wk表示样本分组k的权重，μk表示样本分组k的均值，σk表示样本分组k的协方差，n为全扰动待解释样本的特征维度，x″j表示第k个全扰动待解释样本，k＝1,2,…,m，m表示全扰动待解释样本的数量，k＝1,2,…,k，k为样本分组的数量，上标(■)t表示转置。

29、上述步骤8.3中：

30、样本分组k更新后的权重wk′为：

31、

32、样本分组k更新后的均值μk′为：

33、

34、样本分组k更新后的协方差σk′为：

35、

36、式中，x″j′表示样本分组k中的第j′个全扰动待解释样本，pj′k表示全扰动待解释样本x″j′相对于样本分组k的后验概率，σk表示更新前的样本分组k的协方差，j′＝1,2,…,mk，mk表示样本分组k中全扰动待解释样本的数量，k＝1,2,…,k，k为样本分组的数量。

37、上述步骤9中，样本分组k进行线性回归拟合得到拟合解释模型gk表示为：

38、gk＝βk0+βk1z1+βk2z2+…+βknzn

39、式中，zn表示全扰动待解释样本的第n个特征，βkn表示全扰动待解释样本的第n个特征的权重，n＝1,2,…,n，n为全扰动待解释样本的特征向量，k＝1,2,…,k，k为样本分组的数量；

40、样本分组k的拟合解释模型gk的权重向量βk为：

41、βk＝(xktkk)-1kktyk

42、式中，βk表示样本分组k的权重向量，βk是一个(n+1)×1维的向量，其第一行为截距项β0，第2～n+1行分别为βk1，βk2，…，βkn的值；

43、xk表示样本分组k的样本矩阵，xk是一个mk×(n+1)维的矩阵，其每一行为样本分组k的一个全扰动待解释样本，其第一列为常数项1，第2～n+1列分别为样本分组k的全扰动待解释样本的第i个特征的随机扰动特征值；

44、yk表示样本分组k的预测向量，yk是一个mk×1维的向量，其第1～mk行分别为样本分组k的第1～mk个全扰动待解释样本输入到待解释模型所得到的全扰动预测值；

45、上标(■)t表示转置；mk表示样本分组k中全扰动待解释样本的数量。

46、与现有技术相比，本发明具有如下特点：

47、1、提出单特征临界值的概念，通过分析计算得到单特征的临界值作为扰动边界，排除了扰动样本因某一特征扰动过大对解释结果的干扰。

48、2、设计混合概率方法，利用多元正态分布和期望最大化算法，生成多个由线性回归方法组合而成的在局部更逼近待解释模型局部非线性决策边界的解释结果，并将最忠实于原模型，即误差在阈值内的拟合结果作为最终解释。