一种基于管网退化模型的天然气管网供气可靠性评估方法

本发明提供一种基于管网退化模型的天然气管网供气可靠性评估方法，属于天然气管网供气可靠性评估。

背景技术：

1、天然气作为介于传统化石能源和可再生能源之间的低碳清洁能源，同样热值下相比煤炭可减少45％-55％二氧化碳的排放量，目前作为能源系统转型发展中重点推广使用的能源；随着天然气需求日益增长，管网规模逐渐扩大，结构日趋复杂，天然气供不应求的问题逐渐凸显，对经济发展与社会稳定提出了挑战；究其原因，分输站点和管道作为天然气管网的关键传输设备，其性能状态往往会随管网的不断运行而日趋退化，进而导致管网整体性能下降，无法满足日益增长的天然气需求，出现供气短缺现象。

2、目前，管网配备的智能检测设备可以实现管网设备退化状态的准确检测，在管网运行维护方面发挥着重要作用，因此从管网退化状态数据出发，依据管网设备对管网供气能力的影响特性，构建站点和管道同时退化影响的管网性能评估模型，并根据管网性能评估结果制定科学维修策略，是解决管网供气短缺问题的有效途径；针对天然气管网，管网可靠性可分为结构可靠性和供气可靠性，其中结构可靠性侧重于评估管网设备保持完整功能的概率，而供气可靠性侧重于评估管网供气量满足用户需求的能力；从管网结构来看，管网设备的敷设具有一定的冗余性，某一设备的退化甚至失效并不一定会影响整个管网供气量；管网的首要任务是不间断地供应满足用户需求的天然气，因此基于管网更多强调满足末端用气的任务性，供气可靠性更适用于管网可靠性评估。

3、近年来针对管网供气的可靠性评估进行的研究，大体可归纳为管网退化模型的建立，管网供气量的求解和管网供气可靠性的评估三个步骤，从管网退化模型来看，多以管道和压缩机站作为影响管网供气可靠性的关键设备，将两类设备的退化状态划分为离散多状态，并假设管道容量与退化状态之间存在对应关系；如su等和fan等认为管道和压缩机站可能处于正常、退化和失效三种状态，利用马尔可夫过程描述其随机退化过程；yu等也将两类设备的退化状态做类似划分，但选用蒙特卡罗方法模拟管网状态转换过程；chen等和yang等假设管道和每台压缩机具有正常和失效两种状态，则由压缩机并联组成的压缩机站退化状态可划分为离散多状态，并将管道和压缩机站的退化过程建模为马尔可夫过程。此外，在工程实践中，压缩机站可看作n中取k的冷备用系统，受站点内压缩机退化影响的周边管道容量可分为多个离散阶段。因此，将站点退化状态划分为离散多状态是合理的。然而，腐蚀是管道失效的主要原因之一，并且管道腐蚀退化具有连续单增特性。随着管道腐蚀深度的逐渐增加，管道的最大允许运行压力逐渐降低，从而使管道输气能力逐渐下降。因此，管网供气量受管道腐蚀退化的影响呈现连续降低的变化趋势，将压缩机站和管道退化过程分别建模为离散和连续随机过程，并在此基础上构建与两类设备退化状态对应的随机容量模型，更能准确描述管网供气量在两类设备同时退化影响下的渐变过程。

4、从管网供气量的求解方法来看，学者们或采用仿真的方法模拟不同工况下管网供气量，或采用解析方法求解管网各种退化状态对应的实际供气量。如su等通过仿真软件tgnet实现管网的热-水力模型，模拟管网不同退化状态下的供气量。yu等采用商业软件sps分析管网退化到不同状态后实际供气量的变化规律。yu等建立了考虑用户重要性、水力和压力约束以及设备失效对管网供气量耦合效应的液压模型，并用混合整数线性规划方法求解。chen等引入最大流算法求解管道和压缩机站同时退化影响下的管网实际供气量。yang等考虑用户供气优先顺序，借助最大流算法完成管网供气分配。事实上，采用模拟仿真的方法求解管网实际供气量，虽然能够较为准确地模拟管网的供气状况，但是考虑到管网运行状态的不确定性，巨大的计算负担将使供气可靠性评估模型效率低下。

5、从管网供气可靠性的评估方法来看，大多数学者从不同角度建立了供气可靠性的评价指标。如su等从管网和用户两方面提出管网供气可靠性指标。yu等提出了供气满意度和供气保障能力两个可靠性指标来量化供气能力。yu等从数量和时间的角度建立基于需求侧分析的管网供气可靠性评价指标。yang等从天然气短缺程度和短缺经济损失的角度提出了管网供气可靠性评价指标。fan等从管网和用户两方面，建立考虑供应短缺事件发生概率和后果的供气可靠性评价指标。

6、然而，依据评价指标完成管网供气可靠性的评估离不开对管网运行状态的大规模抽样分析，计算成本较高；为此，chen等基于马尔可夫过程和可靠性理论计算了管网在各种运行场景下的概率，选择了发生概率较高的场景进行供气可靠性评估，但是只关注高概率场景可能会忽略了低概率高后果的极端事件对管网供气安全的影响，低估了天然气管网的潜在风险；因此，现阶段需要综合考虑管网的各个退化状态的概率和相应状态下管网的供需关系，重新全面评估管网供气可靠性。

技术实现思路

1、本发明为了克服现有技术中存在的不足，所要解决的技术问题为：提供一种基于管网退化模型的天然气管网供气可靠性评估方法。

2、为了解决上述技术问题，本发明采用的技术方案为：一种基于管网退化模型的天然气管网供气可靠性评估方法，包括如下的评估步骤：

3、步骤一：考虑天然气管网系统具体受到压缩机站和管道随机退化因素的影响，根据两者退化情况对天然气管网系统供气量的不同影响规律，分别对压缩机站和管道随机退化过程进行建模；

4、步骤二：分析计算管网各种运行状态下的概率，并基于获得管道和压缩机站退化影响下的管网最大供气量，评估管网在各种状态下的供求关系，从而评估管网供气可靠性，具体包括：

5、步骤2.1：针对压缩机站进行可靠性评估；

6、步骤2.2：针对考虑容量的管道进行可靠性评估；

7、步骤2.3：针对管网供气可靠性进行评估；

8、步骤2.4：针对考虑压缩机站和管道退化更新的管网供气可靠性进行评估。

9、所述步骤一中对压缩机站退化过程进行建模的具体方法为：

10、步骤1.1：针对管网系统进行描述表达，采用以下公式表示简化的天然气管网拓扑结构：

11、g≡(v，s)；

12、其中，v＝{1，2，…，n}是管网中所有n个节点的集合，每一个节点代表一个压缩机站，s＝{(i，j)|i，j∈v}是管网中所有m条边的集合，每一条边代表一段天然气管道；

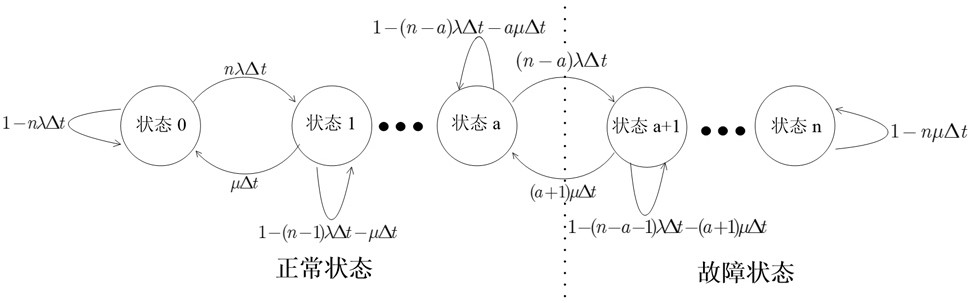
13、步骤1.2：定义每个压缩机站由n台相同压缩机并联组成，其中有n-a台运行压缩机和a台冷备用压缩机，每台压缩机都有正常和故障两种状态，具体以压缩机站中故障压缩机台数定义整个站点的状态：

14、用随机过程{xi(t)，t≥0}表示压缩机站i的退化过程；

15、其中，xi(t)表示压缩机站i在时刻t的状态，满足xi(t)∈{0，1，2，…，n}；

16、当发生故障的压缩机台数从0到a看作压缩机站的正常工作状态，记为：

17、w＝{0，1，…，a}；

18、当发生故障的压缩机台数大于备用压缩机台数时，即发生故障的压缩机台数从a+1到n看作压缩机站的故障状态，记为：

19、f＝{a+1,a+2，…，n}；

20、设定每个压缩机的故障时间和维修时间满足指数分布，将故障率和修复率分别用λ和μ表示，

21、对压缩机站的状态演化使用马尔可夫过程来描述，将压缩机站的转换速率由矩阵a表示为：

22、

23、则将马尔可夫过程的矩阵形式表示为：

24、

25、其中，p(t)＝(pj(t))表示压缩机站在时间t处的状态概率向量，且pj(t)＝p{xi(t)＝j}。

26、所述步骤一中对管道随机退化过程进行建模的具体方法为：

27、步骤1.3：针对管道退化过程进行建模：

28、定义管道(i,j)在时间t处的最大腐蚀深度记为：di,j(t)；

29、设定腐蚀深度的变化符合gamma过程，其概率密度函数的表达式为：

30、

31、其中，

32、步骤1.4：针对随机容量进行建模：

33、采用有限元模型，在ansys软件中采用弧长法，得到管道在不同腐蚀状态下所能承受的最大压力值，表达式为：

34、

35、其中，pi,jcor(t)表示在时刻t腐蚀管道(i,j)所能承受的最大压力，p0为完好管道的最大承受压力，wt为管道的壁厚，a1,a2为待定常数，c2＝a1p0-a2p0也为常数；

36、定义处于节点i的压缩机站正常工作时，则管道(i,j)入口的最大允许压力为其在当前腐蚀状态下所能承受的最大压力，记为pi,jcor(t)；

37、将管道(i,j)出口与压缩机站相连，其出口的最小允许压力为压缩机站j的最小进站压力pc，其中pc是由压缩机站性能决定的常数；

38、定义管道(i,j)在t时刻的容量ci,j(t)的计算公式为：

39、

40、其中，f为常数，pi,jcor(t)为管道(i,j)所能承受的最大压力，但其值不能大于管道的设计压力，pc为压缩机站的最小进站压力，d为管道内径，λ为摩阻系数，δ为气体相对密度，j为气体压缩因子，t0为管道的平均温度，li,j为管道(i,j)的长度；

41、根据承受的最大压力值和容量计算情况，可得管道容量ci,j(t)和最大腐蚀深度di,j(t)之间的函数关系为：

42、

43、其中，c4＝pc2均为常数；

44、联合最大腐蚀深度di,j(t)的概率密度函数，得到管道容量ci,j(t)的概率密度函数的表达式为：

45、

46、其中，为常数。

47、所述步骤2.1中针对压缩机站进行可靠性评估的具体方法为：

48、定义若压缩机站初始状态的状态概率向量满足则压缩机站i的可靠性是直到时刻t压缩机站一直处于正常工作状态的概率，即满足：

49、

50、式中的pj(t),j∈w满足下式所示的微分方程组：

51、

52、其中，pw(t)＝(p0(t),p1(t),…,pa(t))表示压缩机站t时刻处于工作状态的概率向量，为矩阵a的分块矩阵，矩阵b为矩阵a中的分块形式，表示压缩机站的状态在转换前后均处于正常工作状态，矩阵b的具体形式表达为：

53、

54、针对上述微分方程组两端进行拉普拉斯变换，求解得到：

55、

56、其中，i为单位矩阵；

57、将上式代入压缩机站i可靠性的计算公式中，计算可得：

58、

59、其中，ew为分量均为1的a+1维列向量；

60、对上式中的进行拉普拉斯逆变换，即可得压缩机站i在t时刻的系统可靠性，记为：

61、所述步骤2.2中针对考虑容量的管道进行可靠性评估的具体方法为：

62、定义在t＝0时刻，管道(i,j)以全新状态投入运行，腐蚀深度记为di,j(t)＝0，并将管道此时的管道可靠性记为

63、当管道运行至t时刻，管道腐蚀深度为di,j(t)，此时管道的最大容量为ci,j(t)，即当管道(i,j)的输送任务小于等于容量ci,j(t)时，管道能够保持可靠运行，则综合考虑腐蚀深度di,j(t)的所有情况，则管道(i,j)在t时刻可靠性的计算公式为：

64、

65、其中，l为管道的腐蚀失效阈值。

66、所述步骤2.3中针对管网供气可靠性进行评估的具体方法为：

67、对管网的最大流量进行计算，输入为各管段容量矩阵，记为c＝(ci，j(t))n×n；

68、其中，元素ci,j(t)为管道和压缩机站退化影响下管道(i,j)的容量；

69、若节点i,j间没有管道连接，则记为：ci,j(t)＝0；

70、计算管网在t时刻的最大流量g(t)，具体由以下数学优化模型求解：

71、目标：

72、

73、约束：

74、0≤qi,j(t)≤ci,j(t)；

75、

76、其中，qi,j(t)为管道(i,j)的实际流量，s为管网的超级源点，e为管网的超级汇点；

77、约束式中分别表示：管道实际流量qi,j(t)不能超过管道容量限制；

78、对于中间节点i，所有流入节点i的流量等于所有流出节点i的流量；

79、管网中所有从超级源点s流出的流量等于所有汇入超级汇点e的流量；

80、定义评估的管网供气可靠性具体为：在管网每种退化状态下，管网最大供气量为g(t)的概率乘以最大供气量g(t)大于等于总需求z(t)的概率，具体计算步骤为：

81、管网最大供气量为g(t)概率的计算公式为：

82、

83、其中，函数表示考虑管道串并联关系的可靠性，为节点i处t时刻压缩机站的可靠性，函数表示考虑压缩机站串并联关系的结构可靠性；

84、设定管网总需求z(t)的概率密度函数为fz(z(t))，则最大供气量g(t)大于等于总需求z(t)的概率的表达式为：

85、

86、综上，针对管网供气可靠性的表达式为：

87、

88、所述步骤2.4中针对考虑压缩机站和管道退化更新的管网供气可靠性进行评估的具体方法为：

89、设定管道在实际环境中体现出的退化差异性，只影响gamma过程的尺度参数β，对形状参数没有影响，利用贝叶斯更新过程更新尺度参数β，并考虑共轭分布族来简化参数后验分布的解析求解：

90、设定尺度参数β的先验分布为gamma分布，记为ga(up,vp)，在检测时刻t＝lt,l＝1,2,…，获得管道最大腐蚀深度数据为然后结合管道(i,j)在上一检测时刻t＝(l-1)t的状态数据d(l-1)，获得管道(i,j)的增量数据具体计算步骤为：

91、采用贝叶斯更新定理，基于β(l)的先验分布f(β(l))和相应的极大似然函数可得到β(l)的后验分布，表达式为：

92、

93、其中，当l＝1时，f(β(l))为β的先验分布ga(up,vp)，当l>1时，f(β(l))同时也是β(l-1)的后验分布，基于上式得到β(l)的后验分布为：

94、

95、设定各管道的腐蚀退化相互独立，结合β(l)后验分布的表达式，得到管道(i,j)在t时刻的预测可靠性为：

96、

97、针对压缩机站在检测周期内新增的压缩机故障台数遵循参数为λ的泊松分布，泊松分布与gamma分布为共轭分布，故设定λ的先验分布为ga(uc,vc)；

98、在时刻k＝1，2，…获得压缩机站的状态数据，记为

99、其中，表示第i个压缩机站在第k次检测时的压缩机故障台数；

100、结合上一检测时刻压缩机站的状态数据x(k-1)，获得压缩机站i的新增故障台数记为

101、利用贝叶斯更新定理，根据λ(k)的先验分布f(λ(k))和相应的极大似然函数可得到λ(k)的后验分布，表达式为：

102、

103、其中，当k＝1时，f(λ(k))为λ的先验分布为ga(uc,vc)，当k>1时，f(λ(k))同时也是λ(k-1)的后验分布，基于上式得到λ(k)的后验分布为：

104、

105、将更新后的故障率λ(k)代入矩阵b，得到更新后的转移速率分块矩阵，表达式为：

106、

107、根据更新后的转移速率分块矩阵b(k)和当前时刻的状态进一步计算压缩机站i在t时刻的预测可靠性计算公式为：

108、

109、其中，为拉普拉斯逆变换，pw(t)为压缩机站i在t时刻的状态概率向量。

110、本发明相对于现有技术具备的有益效果为：本发明通过提出一种基于管网退化模型的天然气管网供气可靠性评估方法，对天然气管网供气可靠性进行准确评估和预测，可以准确评估当前管网输气能力和预测未来管网供气可靠性的变化趋势，大幅降低供气短缺事件造成的经济损失，并为管网运行维护提供准确的维修依据，确保管网保持高供气可靠运行，保障天然气管网实现持续保畅保供，同时能够降低天然气公司的运营维修成本，增加企业效益。