基于KAN和自适应梯度优化的神经网络参数搜索算法

本发明属于深度神经网络参数搜索，特别涉及一种基于kan和自适应梯度优化的神经网络参数搜索算法。

背景技术：

1、深度神经网络被广泛应用于分类和回归问题，并且通过神经网络结构搜索和参数搜索等进行优化模型参数。反向传播是深度神经网络应用最广泛的参数搜索技术之一，也是卷积神经网络的关键技术，在计算机视觉、自然语言处理和语音识别等研究领域具有显著优势。

2、近年来，人们提出了各种中枢神经网络，如vggnet、resnet等都包含一个全连接层，它们的连接权值通过标准或改进的反向传播技术进行优化，在反向传播技术中采用的梯度下降策略具有收敛速度快的优点。然而，采用反向传播技术的神经网络的全连接层依赖于梯度下降策略，其缺点是容易陷入局部最优。

3、同时，许多进化计算技术被应用于神经网络的参数优化，如粒子群优化、遗传算法、蚁群优化和差异进化等。进化计算可以作为反向传播技术中的无梯度技术使用，它利用种群的优势来实现全局搜索，不需要任何连续的或可微的条件来优化目标函数。但是进化算法并行训练比较昂贵，选择合适的网络大小是一个值得考虑的问题。

4、近期出现的科尔莫戈洛夫-阿诺德网络（kan），它有希望作为多层感知机的替代方案。虽然多层感知机在节点上有固定的激活函数，但 kan在边缘上有可学习的激活函数。每个权重参数都被替换为参数化的样条单变量函数，kan在准确性和可解释性方面都优于多层感知机。因此，如何利用科尔莫戈洛夫-阿诺德网络进行网络结构设计，并结合基于进化计算的全局搜索和反向传播的局部搜索算法，是网络参数搜索的一项挑战。

技术实现思路

1、为解决上述技术问题，本发明提供了一种基于kan和自适应梯度优化的神经网络参数搜索算法，以达到具有更高的效率和搜索性能，能够更快地找到最优的神经网络架构，大大缩减了计算成本的目的。

2、为达到上述目的，本发明的技术方案如下：

3、一种基于kan和自适应梯度优化的神经网络参数搜索算法，包括如下步骤：

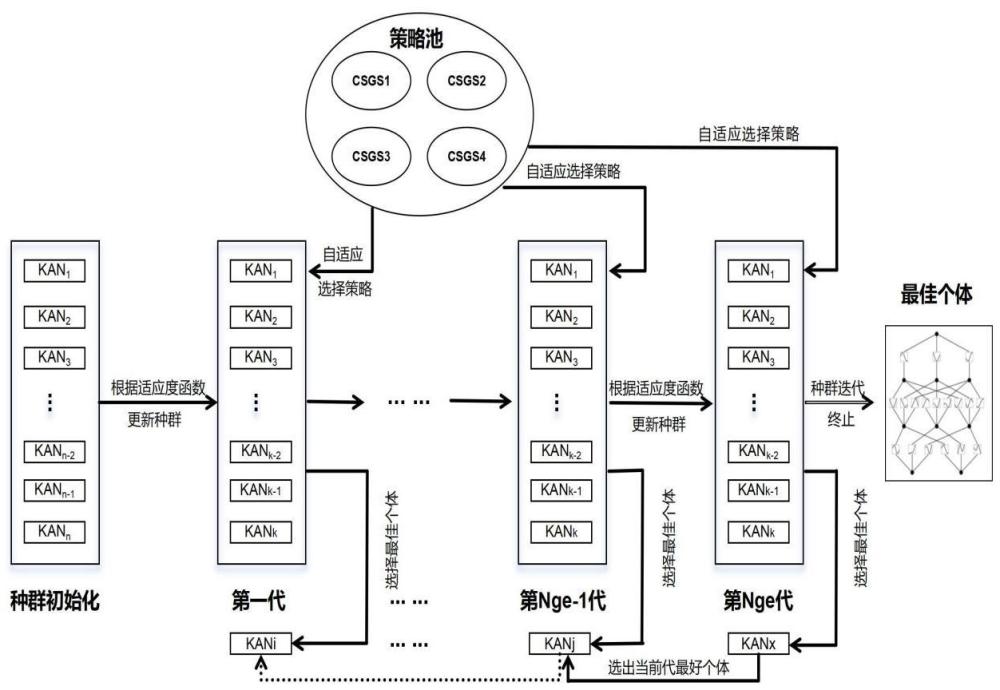
4、步骤1：初始化种群，该种群由n个具有相同初始化参数的kan网络个体组成；

5、步骤2：选择损失函数作为种群评估的适应度函数，将数据样本输入每一个个体中，通过适应度函数得到每个个体的适应度值，根据适应度值选择当前最佳的个体作为初始最优解；

6、步骤3：构造用于种群繁殖的自适应策略池以及策略选择的评价函数；

7、步骤4：根据初始化的种群，每个个体进行网格扩展确定每一个可学习的激活函数，并进行网络结构节点的稀疏化处理和裁剪确定网络形状，以更新种群用于进化的网络结构；

8、步骤5：根据更新的网络结构，每个个体根据构造的评价函数自适应选择策略池中的某个策略进行训练，根据适应度函数计算每个个体的适应度值，并根据适应度值选择一个最佳个体作为当前轮次的最优解；

9、步骤6，迭代步骤4和步骤5直至达到设置的轮次t，最终在t轮次下选出一个最佳网络个体，其具有最优性能的神经网络结构和参数，并作为整个种群的最优解。

10、上述方案中，步骤1中，种群的初始化包括种群大小n、最大迭代次数t、网络深度、每层神经元个数nl、b样条函数阶数k、网格大小g、连接神经元的激活函数，表示示第层kan网络上的第i个神经元的第j个激活函数。

11、上述方案中，一个完整的kan网络个体表示为：

12、；

13、其中，x是输入数据，n是种群中的个体数量，是网络深度，是第n个个体，表示特征矩阵相乘，是第层kan网络的激活函数矩阵，表示如下：

14、；

15、其中，表示第层kan网络上的第个神经元的第个激活函数。

16、上述方案中，步骤2中，种群评估的适应度函数表示为：

17、；

18、其中，s是数据集中的样本数量，是第p个样本的期望值，是kan网络模型第p个样本的实际输出值；

19、把数据样本依次输入到每一个kan网络个体中得到相应的，通过适应度函数计算每个个体的适应度值，选择适应度最低的个体作为初始最优解。

20、上述方案中，步骤3中，选择adam、adagrad、rmsprop和pcgrad四种梯度下降算法分别设置为四种具有不同学习率的策略并放入自适应策略池中。

21、上述方案中，步骤3中，策略选择的评价函数的计算步骤为：

22、（a）计算每种策略在t代之后被种群选择的总次数，表示为：

23、；

24、其中，是策略q在第t代被种群所有个体选择的总次数，是策略q在t代之后被种群所有个体选择的总次数；

25、（b）为了防止策略q在t代之后被种群个体选择的总次数为零，对进行修正；

26、；

27、其中，是一个极小的常数，是的修正结果；

28、（c）计算每种策略在t代之后被种群选择的总次数在所有代种群中的概率，表示为：

29、；

30、其中，是策略q在第t代不被种群个体选择的总次数，是策略q在t代之后被种群所有个体选择的总次数在所有代种群中的概率；

31、（d）计算种群策略选择的评价函数，表示为：

32、；

33、其中，是策略池中梯度下降策略的个数，是策略q在t代之后被选择的总次数占策略池中所有策略的概率，并以此作为策略选择的评价函数。

34、上述方案中，步骤4中，每个个体进行网格扩展确定每一个可学习的激活函数的方法如下：

35、（a）在原始粗粒度网格g1中计算b样条基函数的线性组合表示；

36、；

37、其中，是第个b样条基函数，是第个b样条基函数的权重参数，是原始网格大小，是b样条函数的阶数，即阶为k的b样条函数中包含k个b样条基函数；

38、（b）在扩展后新的细粒度网格g2中计算这些b样条基函数的线性组合表示；

39、；

40、其中，是第个b样条基函数，是第个b样条基函数的权重参数，是网格扩展后的网格大小；

41、（c）通过最小二乘法最小化和之间的距离，得到新的b样条基函数的权重参数以此来更新激活函数；

42、；

43、其中，是最小化和之间的距离训练得到的权重参数。

44、上述方案中，步骤4中，种群中的个体进行网络结构节点的稀疏化处理和裁剪确定网络形状的方法如下：

45、（a）分别计算每个激活函数的l1范数，表示为：

46、；

47、其中，是输入到该激活函数的样本数量，是样本中的数据经过该激活函数后的值；

48、（b）根据获得的每个激活函数的l1范数，分别计算每一kan层所有激活函数的l1范数之和，并计算每一kan层的熵正则化，分别表示为：

49、；

50、其中，是某kan层的所有激活函数l1范数之和，是某kan层的输入节点数，是某kan层的输出节点数，是某kan层中的第i个节点的第j个激活函数的l1范数；

51、；

52、其中，是某一包含个输入节点、个输出节点的kan层的熵正则化；

53、（c）计算用于网络结构稀疏化处理的损失函数并进行训练，表示为：

54、；

55、其中，是包含层kan网络激活函数的l1范数之和，是包含层kan网络激活函数的熵正则化之和，、和是设置的三个超参数，是包含层kan网络的预测损失，表示用于网络结构稀疏化处理的损失函数；

56、（d）计算获得每个节点的传入得分和传出得分，表示为：

57、；

58、其中，是kan网络中第层的第个神经元，是第层所有传入的激活函数l1范数的最大值，是第层第个节点的传入得分；

59、；

60、其中，是kan网络中第层的第个神经元，是第层所有传出的激活函数l1范数的最大值，是第层第个节点的传出得分；

61、如果某节点传入得分和传出得分都大于设置的阈值，则对该节点进行裁剪。

62、上述方案中，步骤5中，根据适应度值选择一个最佳个体作为当前轮次的最优解的方法如下：

63、（a）计算当前轮次种群中所有个体的适应度值；

64、（b）根据个体适应度值选出具有最低适应度值的个体；

65、（c）根据获得个体的适应度值与上一代选出的最佳个体的适应度值进行比较，若小于，则更新为最佳个体。

66、通过上述技术方案，本发明提供的基于kan和自适应梯度优化的神经网络参数搜索算法具有如下有益效果：

67、1、本发明通过高效的科尔莫戈洛夫-阿诺德网络来代替传统的多层感知机，核心是以权重上可学习的激活函数来代替神经元节点上固定的激活函数；

68、2、本发明利用进化算法的思想来优化神经网络参数搜索过程，每次使用梯度下降搜索算法时，无需重新完整训练网络架构，从而大大缩减了计算成本；

69、3、本发明引入了一种非线性自适应机制来优化种群迭代的整个搜索过程，选择adam、adagrad、rmsprop和pcgrad四种梯度下降算法分别转化为四种具有不同学习率的策略并放入自适应策略池中，而不需要用户有先验知识来调整学习率，种群中的个体根据策略选择的评价函数分别选择一个最有利的算法进行参数更新，从而获得最佳个体。

70、综上，本发明基于kan和自适应梯度优化的神经网络参数搜索加速算法不仅具有梯度下降的局部搜索能力，而且具有良好的进化计算的全局搜索能力。