一种无随机数一阶掩码方案的快速构建方法及系统

本发明属于掩码领域，具体涉及一种无随机数一阶掩码方案的快速构建方法及系统。

背景技术：

1、本部分的陈述仅仅是提供了与本发明相关的背景技术信息，不必然构成在先技术。

2、随着物联网技术的快速发展，大量的可连接设备出现在日常生活中。由于可以轻易地接触到，这些设备正在面临一系列的物理攻击，尤其是侧信道攻击。侧信道攻击可以利用设备的功耗，电磁，温度等物理信息来提取设备的秘密信息。

3、为了抵抗侧信道攻击，研究人员提出了大量的对策，其中掩码方案是应用最为广泛的一种。掩码方案是可以使算法运行的中间值独立于秘密变量，以便来打破秘密数据与设备的能量消耗之间的关系。

4、得益于良好的理论基础，门限实现成为一种广泛应用的硬件掩码实现策略。在一个布尔函数的门限实现中，一个秘密变量至少被分为td+1个分量，其中t是布尔函数的代数度，d是掩码方案的安全阶数。由于分量的个数是和代数度和安全阶数相关的，因此一个高代数度高安全阶的门限实现的硬件面积占用是非常大的。

5、为应对硬件资源的问题，一些文献提出了一种只需d+1个分量就可以实现d阶安全性的掩码实现方案。在这个方案中，随机数是必不可少的来保证整个掩码方案的安全性。例如一个一阶安全的二输入的and门要求至少1-bit的随机数。

6、为了摆脱随机数的依赖，shahmirzadi等人在2021年提出了一个方法论来构建2分量的一阶安全的无随机数的掩码方案。在上述工作中，作者给出了很多s-box的无随机数的一阶掩码方案，比如midori，present。发明人注意到上述方案存在两个待改进点：一个是shahmirzadi等人的方法论不能给出prince s-box的无随机数的一阶掩码方案。另一个是构建一个s-box的耗时是比较多的，最长需要30分钟。

技术实现思路

1、本发明为了解决上述问题，提出了一种无随机数一阶掩码方案的快速构建方法及系统，本发明可以快速构建无随机数一阶掩码方案，且具备通用性。

2、根据一些实施例，本发明采用如下技术方案：

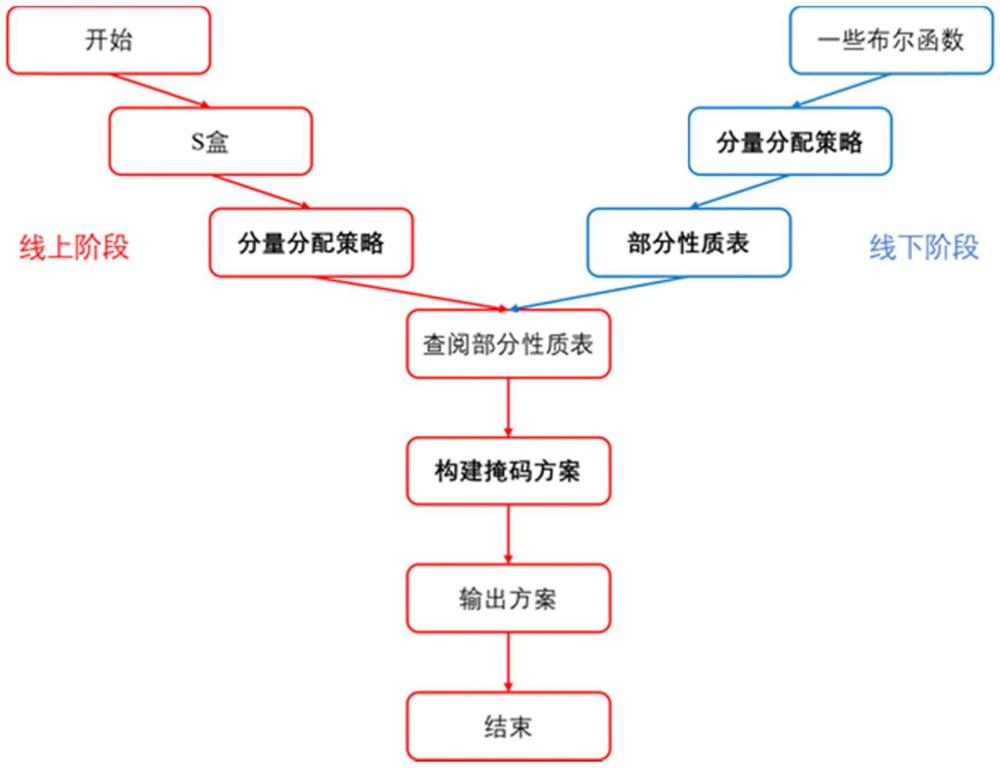
3、一种无随机数一阶掩码方案的快速构建方法，包括以下步骤：

4、基于给定s-box，确定其输入变量的个数以及每一个坐标函数的代数度，根据所述代数度，确定坐标函数中相应代数度的单项式的情况的简记号，根据给定s-box的每一个坐标函数，利用分量分配策略推导出所有可能的分量分配方式；

5、根据所述输入变量的个数、每一个坐标函数的代数度、相应简记号以及相应所有可能的分量分配方式，查阅预先构建的部分性质表，判断掩码性质，得到给定s-box的无随机数的一阶掩码方案；

6、其中，所述部分性质表的构建过程包括确定布尔函数的输入变量个数和代数度，根据输入变量个数和代数度计算相应代数度所有单项式的简记号，根据简记号对应的单项式，推导所有可能的分量分配方式，初始化每一个组分函数，判断掩码性质，存储满足掩码性质的组分函数的组合，形成部分性质表。

7、作为可选择的实施方式，所述部分性质表的构建过程预先在线下进行。

8、作为可选择的实施方式，基于给定s-box，得到给定s-box的无随机数的一阶掩码方案的过程在线上进行。

9、作为可选择的实施方式，所述分量分配策略为推导布尔函数的所有可能分量分配方式的策略，对于布尔函数的各项，以及相应项的各个分量，分配至不同的组分函数中，得到多类不同的分量分配方式，每一类分量分配方式，推导出多个不同的分量分配方式。

10、作为进一步的，每一类分量分配方式，推导出δ个不同的分量分配方式，其中：

11、

12、m是组分函数的数量，是二项式系数。

13、作为可选择的实施方式，查阅预先构建的部分性质表，判断掩码性质的过程中，考虑的掩码性质包括正确性和联合均匀性，其中，正确性要求压缩层的两个输出分量经过异或运算的结果等于s-box的每一个坐标函数；

14、遍历s-box所有的秘密输入和所有的秘密输入的分量，计算得到掩码方案的输出，如果对于每一种秘密输出的情况，它对应所有可能的分量形式的出现次数是相等的，则该掩码方案满足联合均匀性。

15、作为可选择的实施方式，部分性质表的构建过程中，考虑的掩码性质包括独立的联合概率分布和平衡性，其中，独立的联合概率分布为对个各秘密变量的任意取值，各组分函数的联合概率分布是不变；

16、平衡性为无论秘密变量的取值，布尔函数取值为0和1的计数是相同的。

17、作为可选择的实施方式，所述部分性质表为由四个索引构成的查找表t[niv][algdeg][markterms][sat]，其中，niv：目标布尔函数的输入变量的个数，algdeg：目标布尔函数的代数度，markterms：是目标布尔函数中代数度为algdeg的所有单项式的简记号，sat：是上述三个变量确定之后的分量分配方式。

18、一种无随机数一阶掩码方案的快速构建系统，包括：

19、分量分配方式推导模块，被配置为基于给定s-box，确定其输入变量的个数以及每一个坐标函数的代数度，根据所述代数度，确定坐标函数中相应代数度的单项式的情况的简记号，根据给定s-box的每一个坐标函数，利用分量分配策略推导出所有可能的分量分配方式；

20、一阶掩码方案构建模块，被配置为根据所述输入变量的个数、每一个坐标函数的代数度、相应简记号以及相应所有可能的分量分配方式，查阅预先构建的部分性质表，判断掩码性质，得到给定s-box的无随机数的一阶掩码方案；

21、部分性质表构建模块，被配置为确定布尔函数的输入变量个数和代数度，根据输入变量个数和代数度计算相应代数度所有单项式的简记号，根据简记号对应的单项式，推导所有可能的分量分配方式，初始化每一个组分函数，判断掩码性质，存储满足掩码性质的组分函数的组合，形成部分性质表。

22、一种计算机可读存储介质，用于存储计算机指令，所述计算机指令被处理器执行时，完成上述方法中的步骤。

23、一种电子设备，包括存储器和处理器以及存储在存储器上并在处理器上运行的计算机指令，所述计算机指令被处理器运行时，完成上述方法中的步骤。

24、与现有技术相比，本发明的有益效果为：

25、本发明应用分量分配策略，可以构造更多s-box的掩码方案，比如pri nce s-box，通用性强。

26、本发明利用线下阶段和线上阶段相结合的工作方式，在线上阶段给出掩码方案的时间消耗非常短，有效提高了掩码方案构建的效率和速度。

27、为使本发明的上述目的、特征和优点能更明显易懂，下文特举较佳实施例，并配合所附附图，作详细说明如下。

技术特征：

1.一种无随机数一阶掩码方案的快速构建方法，其特征是，包括以下步骤：

2.如权利要求1所述的一种无随机数一阶掩码方案的快速构建方法，其特征是，所述部分性质表的构建过程预先在线下进行；

3.如权利要求1所述的一种无随机数一阶掩码方案的快速构建方法，其特征是，所述分量分配策略为推导布尔函数的所有可能分量分配方式的策略，对于布尔函数的各项，以及相应项的各个分量，分配至不同的组分函数中，得到多类不同的分量分配方式，每一类分量分配方式，推导出多个不同的分量分配方式。

4.如权利要求3所述的一种无随机数一阶掩码方案的快速构建方法，其特征是，每一类分量分配方式，推导出δ个不同的分量分配方式，其中：

5.如权利要求1所述的一种无随机数一阶掩码方案的快速构建方法，其特征是，查阅预先构建的部分性质表，判断掩码性质的过程中，考虑的掩码性质包括正确性和联合均匀性，其中，正确性要求压缩层的两个输出分量经过异或运算的结果等于s-box的每一个坐标函数；

6.如权利要求1或5所述的一种无随机数一阶掩码方案的快速构建方法，其特征是，部分性质表的构建过程中，考虑的掩码性质包括独立的联合概率分布和平衡性，其中，独立的联合概率分布为对个各秘密变量的任意取值，各组分函数的联合概率分布是不变；

7.如权利要求1所述的一种无随机数一阶掩码方案的快速构建方法，其特征是，所述部分性质表为由四个索引构成的查找表t[niv][algdeg][markterms][sat]，其中，niv：目标布尔函数的输入变量的个数，algdeg：目标布尔函数的代数度，markterms：是目标布尔函数中代数度为algdeg的所有单项式的简记号，sat：是上述三个变量确定之后的分量分配方式。

8.一种无随机数一阶掩码方案的快速构建系统，其特征是，包括：

9.一种计算机可读存储介质，其特征是，用于存储计算机指令，所述计算机指令被处理器执行时，完成权利要求1-7中任一项所述的方法中的步骤。

10.一种电子设备，包括存储器和处理器以及存储在存储器上并在处理器上运行的计算机指令，所述计算机指令被处理器运行时，完成权利要求1-7中任一项所述的方法中的步骤。

技术总结本发明提供了一种无随机数一阶掩码方案的快速构建方法及系统，基于给定S‑box，确定其输入变量的个数以及每一个坐标函数的代数度，根据所述代数度，确定坐标函数中相应代数度的单项式的情况的简记号，根据给定S‑box的每一个坐标函数，利用分量分配策略推导出所有可能的分量分配方式；根据所述输入变量的个数、每一个坐标函数的代数度、相应简记号以及相应所有可能的分量分配方式，查阅预先构建的部分性质表，判断掩码性质，得到给定S‑box的无随机数的一阶掩码方案。本发明可以快速构建无随机数一阶掩码方案，且具备通用性。技术研发人员：王美琴,吴立轩,樊燕红,史宇翔,王超然受保护的技术使用者：山东大学技术研发日：技术公布日：2024/11/4