一种高热负荷下的轴承漆膜演化预测方法及系统

本发明属于滑动轴承领域，具体涉及一种高热负荷下的轴承漆膜演化预测方法及系统。

背景技术：

1、滑动轴承广泛应用在大型核电装备、航空航天、核电、铁路等高热负荷、恶劣工况的重大装备中，直接影响着机械设备的可靠性与寿命。随着时间的推移和高热负荷的恶劣工况变化，轴承内表面高热负荷区域可能会产生漆膜，进而引起油膜厚度和分布发生变化，导致轴承润滑不足，增加磨损风险。漆膜演化是一个动态过程，存在着产生随后不断堆积和发生剐蹭脱落甚至不断循环的现象，因此漆膜演化的准确预测是一个极大的难题。

2、目前针对漆膜演化形成主要认为是润滑剂降解造成的，且各种金属离子作为催化剂也促进着润滑剂的降解，随着降解的增多，漆膜也在不断沉积，导致沉积峰的出现，因此沉积模型的建立对仿真预测结果的准确性具有决定性的影响。当前主要采用阿伦尼乌斯(arrhenius)方程建立模型，阿伦尼乌斯(arrhenius)方程表征了化学反应的速率常数与温度之间的关系。采用其建立的漆膜沉积速率模型在所有温度下均发生沉积、且不同工作温度下沉积速率基本相同。因此沉积模型的建立仍存在漆膜演化表征难、预测结果误差大的难题。当前迫切需要一个计算高效准确的模型来表征高热负荷下轴承的漆膜演化。

技术实现思路

1、本发明的目的在于提供一种高热负荷下的轴承漆膜演化预测方法及系统，针对高热负荷下轴承漆膜演化表征难、预测结果误差大的难题，提出一种基于激活函数的高热负荷下轴承漆膜演化预测方法。

2、为了实现上述目的，本发明采用如下技术方案：

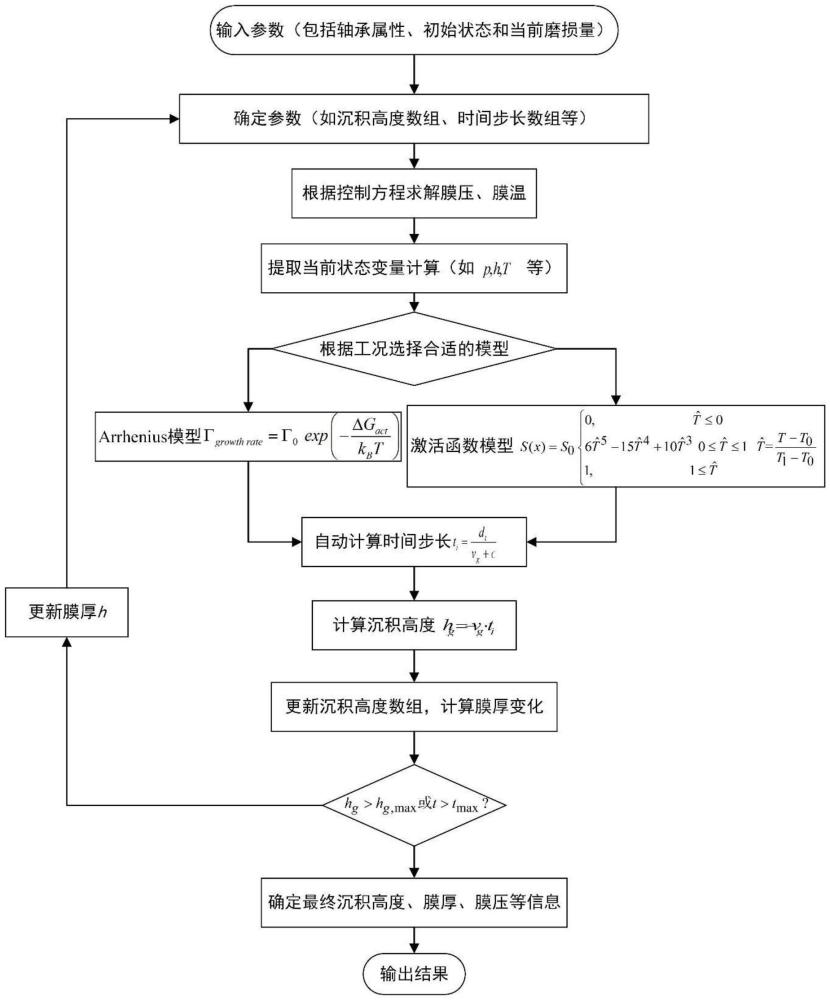
3、一种高热负荷下的轴承漆膜演化预测方法，包括以下步骤：

4、s1、读取输入参数，包括轴承属性、初始状态和当前磨损参数；

5、s2、根据输入参数，初始化相关变量，包括油膜厚度、沉积高度数组、时间步长数组；

6、s3、基于初始化后的相关变量，利用控制方程求解得到轴承当前状态变量膜压、膜温；

7、s4、根据轴承当前状态变量膜压、膜温判断实际轴承工作条件、运行周期与分析需求选择arrhenius模型或激活函数模型求解得到漆膜生成速率；

8、s5、基于漆膜生成速率计算得到当前时间步长

9、s6、基于漆膜生成速率和时间步长，计算得到当前时间步长下的漆膜沉积高度变化量；

10、s7、基于漆膜沉积高度变化量更新漆膜沉积高度数组并计算得到膜厚变化；

11、s8、基于沉积高度计算结果和总时间步长，判断轴承最大沉积高度或总模拟时间是否大于计划高度或时间，如果未满足则更新膜厚h后迭代相关变量，返回s2，若满足则确定最终沉积高度、膜厚和膜压，并输出结果。

12、本发明进一步的改进在于，步骤s3具体包括如下步骤：

13、通过控制方程分别求解雷诺方程和能量方程获得轴承的状态变量即膜压和膜温，求解方法采用有限单元法或有限差分法通用数值求解方法；

14、具体方程形式如下：

15、雷诺方程如下：

16、

17、上式考虑了液膜三个空间方向上变温度下的三维粘度分布：

18、

19、此外，r表示轴承半径；θ表示圆周角；x和y分别代表周向与轴向坐标；u表示轴颈线速度；η、ρ和a分别代表润滑油的粘度、密度和密度比；p和h分别代表油膜压力和厚度；rq为均方根表面粗糙度；为压力流因子，表示粗糙表面油膜平均压力流与光滑表面压力流之比；为剪切流因子，表示因表面相对滑动而由粗糙度的谷峰所带走的附加输送流量；

20、能量方程如下：

21、

22、式中，ρ为介质密度，qp为比热容，u、v、w为x、y、z方向上的速度分量，t为温度，k为热传导系数，ke为y方向的热传导系数，ue为等效黏度。

23、本发明进一步的改进在于，步骤s4具体包括如下步骤：

24、根据轴承当前状态变量判断实际轴承的工作条件、运行周期与分析需求人为选择合适的模型求解漆膜生成速率；可选模型包括arrhenius模型与激活函数模型；选择依据：arrhenius模型在所有温度下均发生沉积，且工作温度下的沉积速率变化幅度小，短运行周期的漆膜沉积模拟选择此模型；激活函数模型通过激活反应温度、饱和反应温度和饱和反应速率三个参数，表征了润滑油温度与漆膜生成速率的关系，能够达到饱和阶段的长运行周期沉积过程选择此模型；

25、模型具体参数如下所示：

26、arrhenius模型：该模型是化学反应速率常数与温度的关系式，在这里表征润滑剂降解产生漆膜堆积速率与温度的关系；具体计算方程如下：

27、

28、其中kb采用下式计算：

29、

30、式中，γ0为初始生成速率，δgact为活化能差，kb为玻尔兹曼常数，t为绝对温标下的温度，a为指前因子/阿伦尼乌斯常数，ea为反应的活化能，r为气体常数；

31、激活函数模型：通过激活反应温度、饱和反应温度以及饱和反应速率的设定，表征了漆膜沉积速率与润滑油温度的关系，具体计算方程如下：

32、

33、式中，s0为初始生成速率，t0为激活反应温度，t1为饱和反应温度，t为润滑油温度，为无量纲温度常数。

34、本发明进一步的改进在于，步骤s5具体包括如下步骤：

35、通过当前膜厚自动计算时间步长，并通过当前最小膜厚求得最大的时间步长，时间步长计算公式如下：

36、

37、式中，dt为特定时间内的漆膜生长厚度，vg表示漆膜生长速率，对应arrhenius模型中的γgrowth rate和激活模型中的s(x)，∈为分母中的稳定项。

38、本发明进一步的改进在于，步骤s6具体包括如下步骤：

39、根据漆膜生长速率和当前时间步长计算漆膜沉积高度，其计算公式如下：

40、hg＝-vg·ti

41、式中，vg表示漆膜生长速率，ti为时间步长。

42、本发明进一步的改进在于，步骤s7具体包括如下步骤：

43、基于沉积高度变化率更新漆膜沉积高度数组并计算膜厚变化，膜厚计算公式如下：

44、h(θ,z)＝cp+hgroove(θ,z)+uj(θ,z)+up(θ,z)+hg

45、式中，θ为周向坐标，z为轴向坐标，hgroove为油槽和几何修形，up为瓦块的力热变形，uj为轴颈的力热变形，cp为轴瓦加工半径间隙，hg为轴承漆膜沉积高度。

46、一种高热负荷下的轴承漆膜演化预测系统，包括：

47、读取模块，读取输入参数，包括轴承属性、初始状态和当前磨损参数；

48、初始化模块，根据输入参数，初始化相关变量，包括油膜厚度、沉积高度数组、时间步长数组；

49、第一计算模块，基于初始化后的相关变量，利用控制方程求解得到轴承当前状态变量膜压、膜温；

50、第二计算模块，根据轴承当前状态变量膜压、膜温判断实际轴承工作条件、运行周期与分析需求选择arrhenius模型或激活函数模型求解得到漆膜生成速率；

51、第三计算模块，基于漆膜生成速率计算得到当前时间步长

52、第四计算模块，基于漆膜生成速率和时间步长，计算得到当前时间步长下的漆膜沉积高度变化量；

53、第五计算模块，基于漆膜沉积高度变化量更新漆膜沉积高度数组并计算得到膜厚变化；

54、判断模块，基于沉积高度计算结果和总时间步长，判断轴承最大沉积高度或总模拟时间是否大于计划高度或时间，如果未满足则更新膜厚h后迭代相关变量，返回初始化模块，若满足则确定最终沉积高度、膜厚和膜压，并输出结果。

55、与现有技术相比，本发明至少具有以下有益的技术效果：

56、1)本发明提供了一种高热负荷下的轴承漆膜演化预测方法，能够实现高热负荷下轴承漆膜随工况、时间、温度的演化预测和轴承性能计算。

57、2)本发明提出了激活函数模型，通过激活反应温度、饱和反应温度以及饱和反应速率的设定，表征了漆膜沉积速率与润滑油温度的关系。

58、3)本发明的设计方法具有简单高效的优点，只需要通过漆膜沉积速率与润滑油温度的关系即可快速直观的获取轴承沉积速率，进而计算漆膜沉积的厚度，省去了繁琐的计算步骤，更加高效。