基于预测变论域模糊PI的伺服系统位置控制方法

本发明涉及一种电机伺服系统的控制方法，具体为一种基于预测变论域模糊pi的伺服系统位置控制方法，属于永磁同步电机伺服系统控制。

背景技术：

1、由于永磁同步电机(pmsm)伺服系统具有良好的控制性能和结构简单等优点，已广泛运用在各类车床、智能生产、航天等装备制造领域中。pmsm的位置伺服控制是实现高性能电机驱动的重要任务之一，位置控制的目标是实时调整永磁同步电机的转子位置，以实现精确的位置跟踪和运动控制。然而，工业系统中往往存在着时变、高耦合、非线性、不确定性等各种复杂的因素，这就给伺服系统的高速、高精度控制造成了不小的挑战。

2、现有技术中，如公告号为cn110716506b所公开的一种基于混合滑模控制的伺服系统位置跟踪控制方法，包括具有外界扰动的永磁同步电机系统模型的建立、基于电机模型的滑模扰动观测器以及二阶超螺旋滑模控制算法的设计。将电机参数和负载转矩的不确定性视为集总扰动，设计了自适应扩展滑模扰动观测器来估计电机参数和负载转矩的不确定性干扰。其次，提出了一种新的终端滑模函数，设计了基于自适应扩展滑模扰动观测器的二阶超螺旋控制器。其中，引入非线性切换项来减弱系统的抖振。进一步证明了终端滑模曲面的收敛性和控制器的稳定性。但在实际的控制系统中，对于永磁同步电机伺服系统，通常采用pi控制方法来实现位置跟踪控制。传统的pi控制方法在控制精度、响应速度、抗干扰能力等方面并不能满足实际需求；模糊pi控制策略结合了模糊控制的非线性控制能力和pi控制良好的适应性，但其性能也受到模糊规则的限制。因此，需要结合其他方法探索简单有效的控制策略，进一步提高控制精度。

技术实现思路

1、本发明的目的就在于为了解决如何采用简单有效的控制策略，进一步提高控制精度的问题而提供一种基于预测变论域模糊pi的伺服系统位置控制方法。

2、本发明通过以下技术方案来实现上述目的：一种基于预测变论域模糊pi的伺服系统位置控制方法，该伺服系统位置控制方法包括以下步骤：

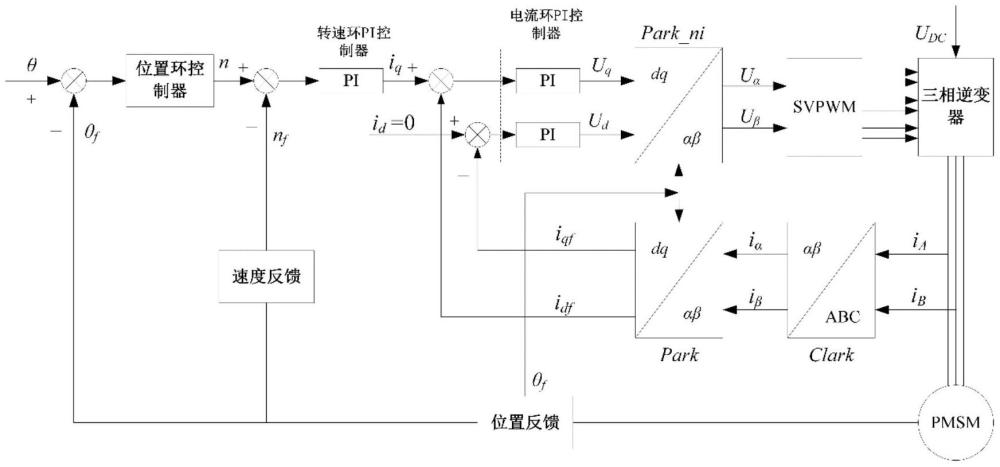
3、步骤一、通过仿真系统分析永磁同步电机的数学模型，根据svpwm空间矢量脉宽调制算法构建pmsm(永磁同步电机)的位置、速度、电流三闭环矢量控制系统，利用位置传感器获得pmsm的实时机械角位移θ，并将其作为反馈调节系统输出；

4、步骤二、给pmsm的伺服系统输入一个目标位置信号，根据伺服系统反馈得到当前误差和误差变化率，并将当前误差和误差变化率输入到位置环控制器中；

5、步骤三、通过位置预测函数模型的预测函数对伺服系统未来的反馈位移进行预测，与预设位移进行比较，进而得到预测位移的误差和误差变化率；

6、步骤四、根据得到的预测位移的误差和误差变化率，通过麻雀搜索算法得到当前最优的变论域模糊控制器论域的伸缩因子，调整模糊控制器论域，得到优化后的模糊pi控制器；

7、步骤五、通过优化后的模糊pi控制器，调整pi参数；

8、步骤六、预测位移的误差和误差变化率输入到调整后的位置环控制器后，伺服系统进行响应调节误差。

9、作为本发明再进一步的方案：步骤一中，建立的永磁同步电机的数学模型如下：

10、

11、式中：ud、uq和id、iq分别为在d–q轴上的定子电压和电流分量，ld、lq分别为d–q两轴上的电感分量，ωe为转子的电角速度，rs为定子电阻；φf为永磁体磁链，ωr为机械角速度，np为极对数，te为电磁转矩，tl为负载转矩，j为转动惯量，b为摩擦系数，θ为电机转子位置。

12、作为本发明再进一步的方案：步骤一中，仿真系统包括电流pi控制器、转速环pi控制器、svpwm空间矢量脉宽调制算法以及位置环控制器。

13、作为本发明再进一步的方案：步骤三中，位置预测函数模型如下：

14、

15、式中：ts为控制周期和预测步长；分别为定子电流d、q轴分量的预测值；为转子速度预测值，θp(k+1)为转子位移预测值，由此进行滚动优化，预测未来时刻的位移。

16、作为本发明再进一步的方案：步骤三中，将预测得到的位移与设定位移进行对比，得到预测位移的偏差ep和偏差变化率ecp。

17、作为本发明再进一步的方案：步骤四中，麻雀搜索算法为：

18、麻雀搜索算法的种群为x，待优化变量参数为d，种群发现者的位置更新公式为：

19、

20、式中：t为当前迭代次数；j＝1，2，3，…，d；xk,j为第k只麻雀在第j维中的位置；α为随机数；tmax为最大迭代次数或最大循环次数；r2为预警值；d为安全阈值；q为服从正态分布的随机数；l为1×d的单位矩阵；

21、种群中跟随者的位置更新可描述为：

22、

23、式中：xw为当前整个种群全局最差的位置；xp为目前发现者所占据的最优位置；a为1×d的矩阵，其中每个元素随机赋值为1或-1，并满足式a+＝at(aat)-1；

24、麻雀种群中警戒者位置更新公式为：

25、

26、式中：xb为当前麻雀种群的全局最优位置；χ为服从标准正态分布的随机数；fk为当前麻雀个体的适应度值；fg为当前麻雀种群全局最佳的适应度值；k为在范围[-1，1]之间的随机数；fw为当前麻雀种群全局最差的适应度值；ε为很小的非零常数，判断算法是否达到最大迭代次数，满足则退出，否则重新计算麻雀的适应度值，最终输出待求变量的最优解。

27、作为本发明再进一步的方案：步骤四中，变论域模糊控制器为双输入控制系统，根据输入的变量偏差e与偏差变化率ec均会作用于伸缩因子，定义输入输出量的论域如下：

28、

29、式中：α，β分别为输入变量偏差e和偏差变化率ec的伸缩因子，[-e,e]和[-ec,ec]分别为两者的初始论域；论域随着偏差的变化而自适应地变化；当偏差大时，论域膨胀，搜索范围扩大，以提高系统的动态响应速度；当偏差小时，论域压缩，搜索范围缩小，以提高系统的控制精度。

30、作为本发明再进一步的方案：步骤五中，模糊pi控制器中模糊语言变量设为{nb,nm,ns,zo,ps,pm,pb}，其中，nb、nm、ns、z、ps、pm、pb分别代表负大、负中、负小、零、正小、正中、正大。

31、作为本发明再进一步的方案：步骤五中，模糊pi控制器采用mamdani型模糊推理系统，pi参数整定公式为：

32、kp＝kp0+δkp

33、ki＝ki0+δki

34、式中：kp0、ki0均为pi参数的初始设定值；δkp、δki均为模糊控制pi解算出的动态整定值，kp为比例系数，ki为积分系数，系统的实际输出值为：

35、

36、本发明的有益效果是：通过结合麻雀搜索算法与变论域模糊控制器，对传统pi控制器进行改进，实现对永磁同步电机的精确控制，提高伺服系统的位置控制性能，再引入模型预测函数对位移进行预测，以预测信息作为优化模糊控制参数和pi控制参数的输入，实现模糊控制器论域的超前调整，提高了系统对强时变性和非线性的适用性以及提高了系统的稳定性。