一种基于图分割的多阶段交叉聚类异常数据检测方法

本发明属于数据交叉聚类，涉及一种检测方法，具体涉及一种基于图分割的多阶段交叉聚类异常数据检测方法。

背景技术：

1、聚类是在不访问数据标签的前提下，使在同一簇的数据尽可能的相似，不同簇的数据尽可能的不相似。传统聚类方法大多将样本单一的分为某一类，然而在真实数据中，一个样本不仅仅只能属于一类，它同时可以属于多个类。比如手机壳，既属于电子附属品也是时尚单品。再如社会关系、病情发展、生物演化等特定情境下，属于多个类的样本对其所属的各类有衔接、联系的特殊作用，尤其是对这些类中只属于某个类的样本。如类a、c所属的交集都有包含样本群b，则此时通过b的衔接类a、c间接的存在关系。针对聚类分析这一实际应用的缺陷和问题，如是更侧重于综合分类的多属性交叉聚类被提出。

2、交叉聚类是在聚类方法基础上的一个重要发展，旨在克服传统聚类方法只能将数据划分为互斥簇的局限性。交叉聚类允许样本同时属于多个类，一方面这种灵活性更能适应现实生活中的复杂关系和模式，另一方面可以更好地解释数据点与簇之间的关系。但是交叉聚类问题中的簇边界通常模糊不清且一个数据点可以同时属于多个簇，这给准确划分簇的边界带来巨大困难。然而图分割方法本身就具有划分图和灵活处理重叠关系的能力，所以基于这些能力，图分割可以适用于各种类型数据的聚类场景，不受簇形状和结构的限制，能够发现复杂的簇结构和关系。

3、虽然基于图分割的交叉聚类方法已经取得了一定的进展，但仍然存在一些挑战和不足之处，如：已有的基于图分割的交叉聚类方法受聚类形状、聚类密度的影响较大；有的算法有较高的效率，但是无法找到最优的分割，有的算法有较高的分割质量，但是需要较多的时间和空间。

技术实现思路

1、针对现有技术中的上述不足，本发明提供的一种基于图分割的多阶段交叉聚类异常数据检测方法，解决了现有技术中对异常数据检测不准确的问题。

2、为了达到上述发明目的，本发明采用的技术方案为：一种基于图分割的多阶段交叉聚类异常数据检测方法，包括如下步骤：

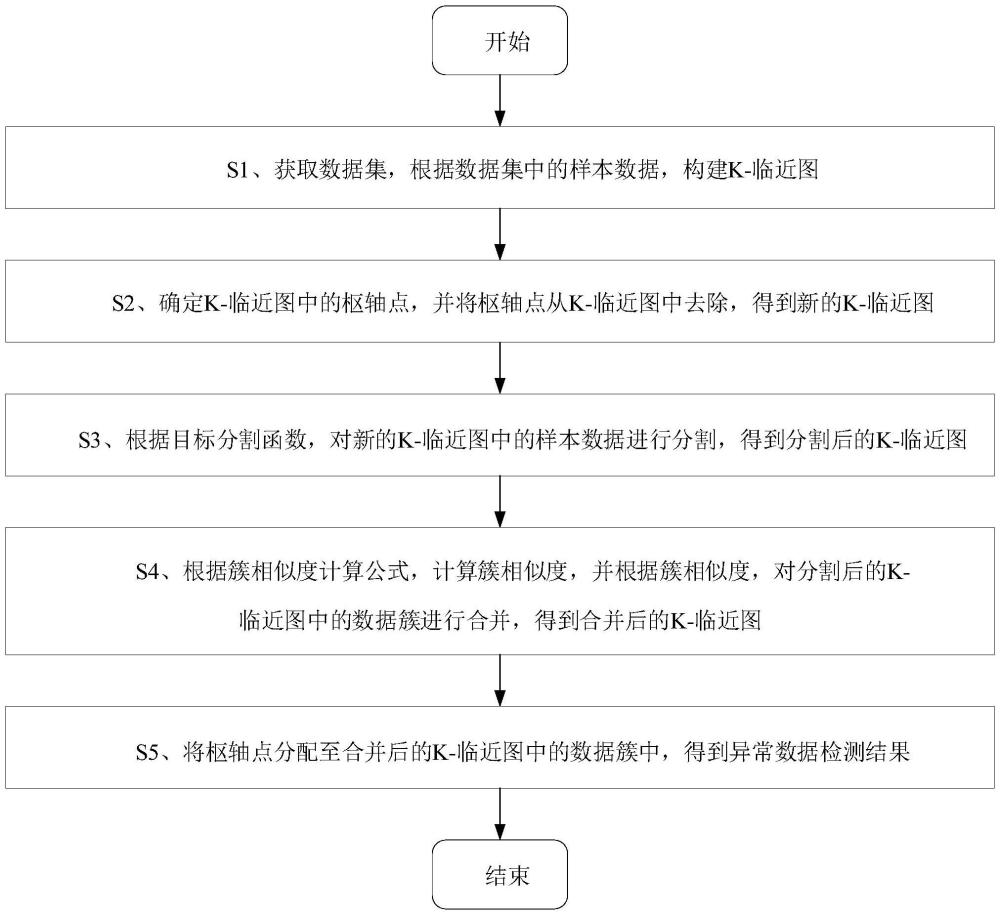
3、s1、获取数据集，根据数据集中的样本数据，构建k-临近图；

4、s2、确定k-临近图中的枢轴点，并将枢轴点从k-临近图中去除，得到新的k-临近图；

5、s3、根据目标分割函数，对新的k-临近图中的样本数据进行分割，得到分割后的k-临近图；

6、分割后的k-临近图中包括至少两个数据簇；

7、每个数据簇中包括至少两个样本数据；

8、s4、根据簇相似度计算公式，计算簇相似度，并根据簇相似度，对分割后的k-临近图中的数据簇进行合并，得到合并后的k-临近图；

9、s5、将枢轴点分配至合并后的k-临近图中的数据簇中，得到异常数据检测结果。

10、上述方案的有益效果是：本发明以现有的基于图分割的交叉聚类算法为基础，引入图分割的多阶段思想，对分割过程进行重构；在合并过程中使用图连通的相似度函数，用以进一步提高交叉聚类的质量，减少图形状和密度的影响，在运算效率上，引入图连通的目标函数和快速迭代方法，用以提升计算效率；可以大幅提升异常数据的判别性，并且具有较好的性能。

11、进一步地，步骤s2中，确定k-临近图中的枢轴点，具体包括：

12、s21、计算k-临近图中每个数据点的密度；

13、s22、确定k-临近图中每个数据点的邻居节点；

14、s23、根据k-临近图中每个数据点的密度和k-临近图中每个数据点的邻居节点的密度，计算k-临近图中每个数据点的局部距离密度比；

15、s24、根据k-临近图中每个数据点的局部距离密度比，使用判断公式，确定枢轴点；

16、判断公式为：

17、

18、其中，la表示判断阈值，r(xi)表示样本xi的局部距离密度比，表示枢轴点的集合。

19、上述进一步方案的有益效果是：使用数据点的密度与它邻居的平均密度之比计算其局部密度比，以反映图的相对稀疏、稠密，并将局部距离密度比较小的点作为枢轴点，并将枢轴点进行去除，可以使得图、簇的形状更加清晰。

20、进一步地，步骤s3中，目标分割函数jcut为：

21、

22、其中，ai表示样本数据xi与同一数据簇中所有其他样本数据的平均距离，bi表示样本数据xi与其它数据簇中所有样本数据平均距离的最小值，n表示样本数据的数量。

23、进一步地，步骤s3中，对新的k-临近图中的样本数据进行分割，具体包括：

24、s31、获取最小化轮廓系数和最大迭代次数；

25、s32、对新的k-临近图中的样本数据进行分割，当最小化轮廓系数收敛或者迭代次数达到最大迭代次数时，结束分割，否则，继续对新的k-临近图中的样本数据进行分割。

26、上述进一步方案的有益效果是：通过最小化轮廓系数的分割方式，使得每个样本尽可能地接近其自身所属的簇，并且尽可能地远离其他簇；这样的聚类方式通常会产生更加紧密且分离度良好的簇；使用最小化轮廓系数做为优化目标，可以鼓励产生更具代表性的簇，从而提高分割质量。

27、进一步地，步骤s4中，簇相似度计算公式为：

28、

29、其中，表示数据簇i和数据簇j之间的相似度矩阵，γ(ci,cj)表示相似度函数，用于衡量数据簇i到数据簇j的连续程度，e表示自然常数。

30、进一步地，步骤s4中，根据簇相似度，对分割后的k-临近图中的数据簇进行合并，具体包括：

31、s41、根据相似度矩阵，确定相似簇对；

32、相似簇对为分割后的k-临近图中相似度最大的两个数据簇；

33、s42、将相似簇对进行合并；

34、s43、更新相似度矩阵，得到更新后的相似度矩阵；

35、s44、判断目标合并函数是否收敛，若是，则结束对分割后的k-临近图中数据簇的合并流程，若否，则重复步骤s41-s44。

36、进一步地，步骤s44中，目标合并函数j为：

37、

38、其中，n表示聚类个数，表示数据簇i和数据簇j之间的相似度矩阵。

39、上述进一步方案的有益效果是：随着合并的不断进行，簇数会越来越小，簇间距离值的个数也会越来越少，可以为样本提供较多的属于多个标签的可能性。

40、进一步地，步骤s5，具体包括：

41、s51、计算枢轴点到合并后的k-临近图中的每个数据簇的距离；

42、s52、将距离中最小距离对应的目标数据簇确定为合并数据簇；

43、目标数据簇为合并后的k-临近图中的数据簇；

44、s53、将枢轴点分配至合并数据簇中，得到异常数据检测结果。

45、进一步地，步骤s51，使用的计算公式为：

46、

47、其中，dist(pg,ci)表示枢轴点到合并后的k-临近图中的每个数据簇的距离，pg表示枢轴点，d(pg,v)表示枢轴点pg到合并后的k-临近图中点v的距离，ci表示合并后的k-临近图中第i个数据簇。

48、上述进一步方案的有益效果是：枢轴点通常代表数据集中的重要特征或关键信息，将枢轴点正确地归类到簇中，可以使聚类结果更具解释性，便于理解和分析。