一种考虑结构面扰动损伤的剪切分数阶本构模型构建方法

本发明涉及岩体结构面工程领域，用于模拟和分析在作用下岩体的微动力扰动损伤劣化行为和剪切扰动特性。

背景技术：

1、在岩体结构面工程中，岩体的损伤和剪切特性对于岩体结构面微动力扰动剪切变形研究和工程稳定性至关重要。大量研究表明岩体结构面扰动变形类似于蠕变行为，根据岩体结构面的变形特征分为三个阶段：减速阶段、等速阶段和加速阶段。减速阶段进入等速阶段需要一定的条件，当满足此条件时，岩体结构面微动力扰动变形进入裂隙稳定扩展阶段；从等速阶段进入加速阶段也需要一定条件，当不满足该条件时，岩体结构面扰动变形趋于稳定，不会发生扰动破坏；满足该条件时，岩体结构面扰动由等速阶段进入加速阶段，岩体结构面内部裂纹扩展加剧，最后岩体结构面发生扰动破坏。然而，传统的岩体剪切模型往往忽略了扰动因素造成的岩体结构面内部劣化损伤且忽视了应变速率与剪切应力呈非线性的影响，导致模拟加速扰动过程结果与实际工程情况存在偏差。

2、分数阶微积分是将整数阶的导数算子推广到任意实数阶的微积分，与传统的弹簧、牛顿黏壶等传统元件相比，分数阶元件具有参数少、物理意义较为明确、可以描述非线性变形等优点。因此，开发一种考虑岩体结构面扰动损伤的剪切分数阶本构模型构建方法，为岩体结构面工程中围岩扰动剪切破坏造成的灾害进行预测和长期稳定性分析提供理论依据。

技术实现思路

1、本发明的目的是提供考虑岩体结构面扰动损伤的剪切分数阶本构模型构建方法，在隧道开挖后该模型能够准确模拟和分析在微动力扰动作用下岩体的损伤行为和剪切特性。

2、为实现上述目的，本发明采用以下技术方案：

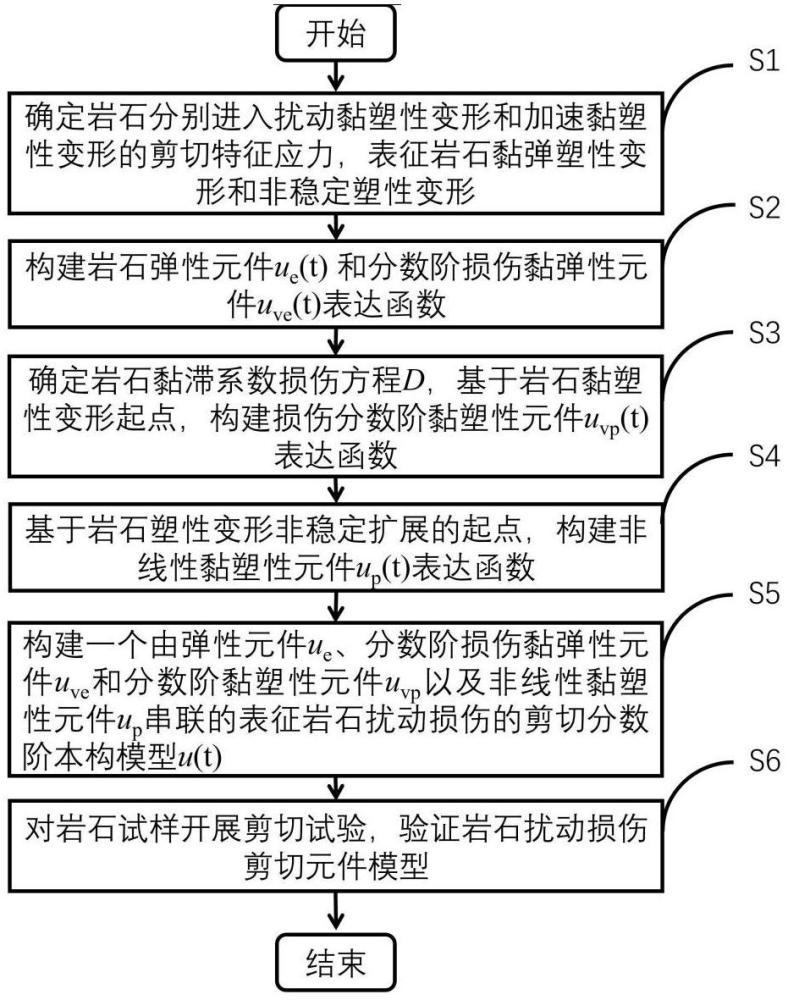
3、s1、确定真三维应力下岩体结构面分别进入扰动黏塑性变形和扰动加速黏塑性变形时刻对应的剪切扰动黏塑性启动应力和剪切扰动黏塑性临界应力，表征启动岩体结构面扰动黏弹塑性变形和扰动非稳定塑性变形；

4、s2、构建岩体结构面弹性元件ue(t)和分数阶损伤黏弹性元件uve(t)表达函数；

5、s3、确定岩体结构面黏滞系数损伤方程d，基于步骤s1中岩体结构面黏塑性变形起点，构建损伤分数阶黏塑性元件uvp(t)表达函数；

6、s4、基于步骤s1中岩体结构面塑性变形非稳定扩展的起点，构建非线性黏塑性元件up(t)表达函数；

7、s5、构建一个由弹性元件ue、分数阶损伤黏弹性元件uve和分数阶黏塑性元件uvp以及非线性黏塑性元件up串联的表征岩体结构面扰动损伤的剪切分数阶本构模型u(t)；

8、s6、对岩体结构面试样开展剪切试验，验证步骤s5中岩体结构面扰动损伤的剪切分数阶本构模型。

9、所述步骤s1中，以岩体结构面剪切扰动应力-应变曲线中岩体结构面进入塑性变形对应的剪切扰动应力作为启动黏塑性变形的剪切扰动黏塑性启动应力τ0，对应的剪切应变为u0；以岩体结构面剪切扰动应力-应变曲线中在第n个(n＞1)中单位时间内应变与单位应力乘积与第n-1个单位时间内应变与单位应力乘积之比大于1.2时对应剪切应力作为表征加速黏塑性变形的剪切扰动黏塑性临界应力τp，对应的剪切应变为up；

10、所述步骤s2中，构建岩体结构面弹性元件ue(n)表达函数：

11、

12、其中g1是弹性剪切模量，τ是岩体结构面试块所受的应力；

13、构建分数阶损伤黏弹性元件uve(n)表达函数：

14、

15、

16、(2)式中左右进行积分并联合(3)式并联合利用n＝tf的关系，采用laplace变换和逆变换确定岩体结构面分数阶黏弹性元件uve(t)的表达式：

17、

18、其中g2是弹性剪切模量，τ是岩体结构面试块所受的剪切应力，是分数阶黏滞系数，α是分数阶阶数。

19、所述步骤s3中，确定岩体结构面黏滞系数损伤方程d，构建损伤分数阶黏塑性元件uvp(n)表达函数的方法为：

20、a1、基于步骤s1中对岩体结构面开展的微动力扰动实验获得的不同幅值和频率下岩体结构面的物理力学参数，获取某种岩体结构面在微动力扰动下的应变率和时间之间的规律并将岩体结构面的变形分为弹性变形εe和微动力扰动塑性变形εp：

21、ε＝εe+εp (5)

22、a2、获得微动力扰动塑性变形εp与幅值、时间、岩体结构面材料特性之间的关系：

23、

24、其中，ek表示微动力扰动作用下的岩体结构面模量；a表示扰动幅值；n表示在微动力扰动下的硬化指数；

25、a3、计算微动力扰动塑性应变单位增量：

26、

27、其中，δt为单位时间；

28、a4、有微动力扰动导致岩体结构面内部造成的损伤为d，导致微动力扰动作用下的模量产生损伤；构建损伤后的模量表达式：

29、

30、a5、根据ek与岩体结构面矿物组成、微扰动幅值和加载时间的关系，假设ek与幅值和加载时间的方程：

31、ek＝ρ·aα·tβ (9)

32、若最终损伤方程表达与实际岩体结构面损伤曲线相符，则该假设成立；

33、a6、构建扰动损伤的单位增量：

34、

35、

36、a7、引入微动力扰动对岩体结构面损伤的影响，构建得到考虑微动力扰动的岩体结构面损伤本构模型：

37、

38、

39、并根据manson-coffin经验公式，构建在微动力扰动作用下塑性应变与微动力扰动幅值的关系函数：

40、

41、其中c表示材料参数；

42、并利用n＝tf的关系，获得微动力扰动作用下岩体结构面损伤本构模型：

43、

44、a8、根据三维应力下扰动剪切强度准则构建屈服函数f(τ)：

45、

46、a9、开展岩体结构面剪切扰动预实验，基于步骤s1所述方法确定剪切扰动黏塑性启动应力τ0，根据τ0的取值和步骤a8中的屈服函数f(τ)，引入perzyna超应力理论的流动规律，确定扰动剪切黏塑性启动屈服函数f1，构建分数阶黏塑性元件本构方程：

47、

48、其中且取f0＝1；

49、a10、将步骤a9中的(17)式左右进行积分，利用n＝tf的关系并采用laplace变换与逆变换的方式确定分数阶黏塑性体剪切扰动本构方程：

50、

51、其中τ是岩体结构面试块所受的剪切应力，ηβ2是分数阶黏滞系数，β是分数阶阶数；

52、所述步骤s4中，基于步骤s1中岩体结构面塑性变形非稳定扩展的起点，构建非线性黏塑性元件up(n)表达函数的方法为：

53、b1、开展岩体结构面剪切扰动预实验，基于步骤s1所述方法确定剪切扰动黏塑性临界应力τp，根据τp的取值和步骤a8中的屈服函数f(τ)，确定岩体结构面在三维扰动剪切作用下进入加速黏塑性变形的屈服临界函数f2；

54、b2、基于步骤b1中在剪切扰动试验中获得的岩体结构面应变与时间、应力与应变之间的关系，明确岩体结构面在不同剪切应力作用下应力速率和时间之间的关系，构建岩体结构面剪切应变速率与应力之间的关系：

55、

56、b3、对步骤b2中(19)式进行积分，引入perzyna超应力理论的流动规律，确定岩体结构面非线性黏塑性元件up(t)的表达式：

57、

58、其中η3是分数阶黏滞系数，n是扰动次数，δ是材料系数，且取f0＝1。

59、所述步骤s5中，基于步骤s1中的岩体结构面黏塑性变形和塑性变形非稳定扩展的起点，构建一个由损伤弹性元件ue(n)、分数阶黏弹性元件uve(n)和分数阶黏塑性元件uvp(n)以及非线性黏塑性元件up(n)串联的表征岩体结构面扰动损伤的剪切分数阶本构模型u(n)：

60、

61、所述步骤s6中，对岩体结构面试样开展剪切试验，验证步骤s5中岩体结构面扰动损伤的剪切分数阶本构模型的方法为：

62、c1、确定岩体结构面的强度破坏判据，根据判据确定岩体结构面剪切扰动元件模型相应的强度阈值；

63、c2、对岩体结构面进行剪切扰动试验，获取岩体结构面剪切扰动试验数据：应力、应变、试验时间；

64、c3、基于步骤c2所获得的试验数据：应力、应变、试验时间，对所述步骤s5中岩体结构面剪切扰动元件模型u(t)进行拟合，获得拟合参数和相关性结果。

65、本发明的有益效果在于：

66、1、本发明通过引入新非线性扰动元件和扰动劣化造成的损伤对剪切本构方程描述岩体结构面受到扰动剪切作用后的非线性扰动变形，特别是关于岩体结构面进入加速扰动阶段。基于此建立能够反映岩体结构面扰动劣化的非线性剪切本构元件模型，模型参数简单，物理学意义明确。

67、2、本发明基于损伤理论，引入损伤变量来描述岩体结构面加载导致的岩体结构面弹性模量变化情况，损伤变量与弹性元件组成弹性模量逐渐减小的损伤弹性元件。

68、3、本发明基于强度准则提出一种考虑岩体结构面非线性应变率的剪切扰动模型构建方法完整表征了真三轴下岩体结构面扰动过程中的衰减扰动阶段、等速扰动阶段和加速扰动阶段三个阶段以及能够准确模拟和分析在时效作用下岩体的损伤行为和剪切特性。

69、4、本发明构建的模型进行二次开发后，可以用于岩体结构面工程设计和分析的准确性并且为岩体工程的安全性和稳定性评估提供有力支持。