一种高精度浮点三角函数的运算装置及方法与流程

本发明涉及浮点数计算领域，特别涉及一种高精度浮点三角函数的运算装置及方法。

背景技术：

1、浮点数运算一直是处理器芯片运算模块设计的重点。近年来，随着科学计算、图形处理和机器学习不断发展，对计算平台处理器芯片性能的要求也不断提高，处理器内部浮点数运算单元（float point unit，fpu）的优化是提升整体芯片性能的关键。ieee 754标准是目前使用最广泛的浮点数标准，其中规定了浮点数的格式、舍入规则、异常处理和算术运算，这为处理器芯片设计中的数学运算提供了一个一致和可靠的框架。

2、三角函数是一类重要函数，包括sin函数、cos函数和arctan函数等，广泛用于复杂算法的计算。但是由于其非线性特性和计算复杂性，难以通过基本运算直接实现，对芯片设计实现提出了一定的挑战。通过在处理器芯片中集成专用的三角函数计算单元，可以显著提升计算效率，减少延迟并降低功耗，从而满足现代高性能计算的需求。

3、坐标旋转数字计算（coordinate rotation digital computer，cordic）算法在处理器芯片设计中被广泛用于计算三角函数，其核心优势在于它能够通过迭代的位移和加法操作计算出函数值，避免使用乘法或除法等占用面积大、功耗高的运算。并且，cordic适合通过流水线和并行处理的方式加速计算，因此常用于高性能处理器和数字信号处理器的设计中，支持实时的三角函数计算需求。

4、虽然cordic算法在处理器芯片设计中具有许多优势，但它也存在一些缺点和局限性，这些缺点在某些应用场景中会影响其使用效果。首先，cordic算法本质上是一种迭代算法，计算结果的精度依赖于迭代次数，对于高精度计算所需的迭代次数较多。因此在高精度设计实现中，收敛速度可能较慢，导致运算延迟增加。其次，cordic算法基于逐步旋转向量的方法来逼近三角函数值，为了避免复杂的乘法和除法操作，通过一系列位移和加法来替代。虽然这样使得硬件实现简单，但这样只能提供有限的精度，不得不通过更多的迭代减少误差。最后，为了适应不同的三角函数计算需求，硬件设计中可能需要实现多个cordic模块或对其进行复杂的控制，这在芯片设计时增加了硬件复杂性和设计成本。

技术实现思路

1、为解决上述技术问题，本发明提供了一种高精度浮点三角函数的运算装置及方法，通过二次多项式分段拟合三角函数，使用二次多项式近似计算三角函数值，避免了传统设计使用cordic进行实现的时间和面积成本，同时可以更精确地逼近三角函数真实值，在处理器芯片设计实现中优化了三角函数的计算速度、计算精度与资源占用。

2、为达到上述目的，本发明的技术方案如下：

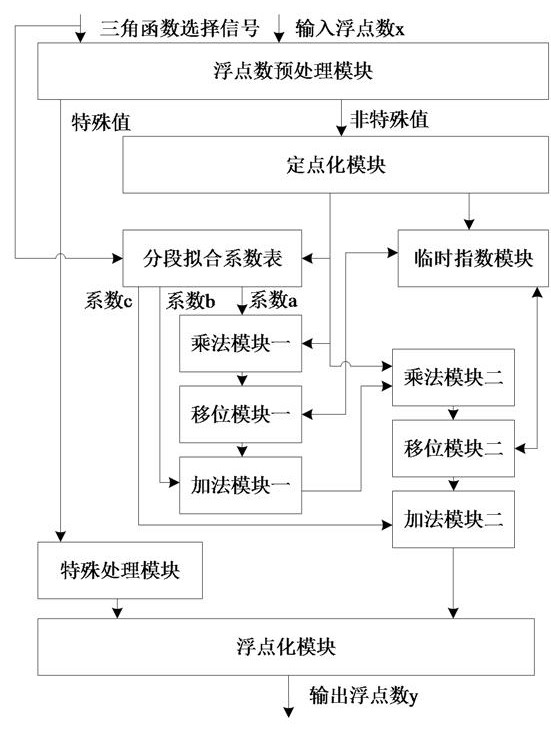
3、一种高精度浮点三角函数的运算装置，包括浮点数预处理模块、定点化模块、分段拟合系数表、临时指数模块、乘法模块一、乘法模块二、移位模块一、移位模块二、加法模块一、加法模块二、特殊处理模块和浮点化模块；

4、所述浮点数预处理模块的输入为浮点数x和三角函数选择信号，该模块根据三角函数选择信号过滤非法输入和输入中无需运算的特殊值，将特殊值送至特殊处理模块，由特殊处理模块判断特殊值类型，直接输出对应的函数值；如果输入为非特殊值，则送至定点化模块；

5、所述定点化模块的功能是对浮点数x进行浮点转定点，将转换的定点数发送给分段拟合系数表、乘法模块一和乘法模块二，将转换的临时指数送至临时指数模块进行存储；

6、所述分段拟合系数表中存储了sin、cos和arctan函数拟合得到的放大后的多项式系数a、b、c，供乘法模块一、加法模块一、加法模块二使用；

7、所述乘法模块一中进行系数a乘以x的运算，并将定点数积运算结果ax送至移位模块一；

8、所述移位模块一对ax右移或左移指定的位数，使其与b保持相同的放大倍数，并将结果送至加法模块一；

9、所述加法模块一中进行ax加b的运算，并将运算结果送至乘法模块二；

10、所述乘法模块二中进行(ax+b)乘以x的运算，乘法模块二的结构与乘法模块一结构相同，得到的结果送至移位模块二中；

11、所述移位模块二对(ax+b)x结果右移或左移指定的位数，使其与c保持相同的放大倍数，并将结果送至加法模块二；

12、所述加法模块二中进行((ax)+b)x+c的运算，结果送至浮点化模块；

13、所述浮点化模块用于将整形数转换为浮点数后输出浮点数y。

14、上述方案中，所述非法输入为不在函数定义域内的所有值，对于sin和cos函数来说，特殊值包括0、±0.25的整倍数以及超过2^23次方的值，这时的函数值为±1或0。

15、上述方案中，所述定点化模块中，浮点数转定点过程首先确定目标定点格式的位宽，然后将浮点数的符号位映射到定点数的符号位，再根据浮点数的指数值，通过左移或右移操作来缩放小数位部分，使数据符合定点表示精度。

16、上述方案中，所述定点化模块中，当运算sin和cos函数时，有如下处理流程：

17、（1）如果指数小于125，则输入在0到0.25之间，直接输出小数部分；

18、（2）如果指数等于125，则输入在0.25到0.5之间，对小数部分进行取反加1并输出；

19、（3）如果指数等于126，则输入在0.5到1之间，判断小数部分最高位：如果小数部分最高位为1，则输入符合0.75到1之间，对小数部分最高位置0，对剩余部分取反加1并输出；如果小数部分最高位为0，则输入符合0.5到0.75之间，直接输出小数部分；

20、（4）如果指数大于126，则输入大于1，对小数部分左移指数与126的差值，判断左移后的小数部分首位与第二位：如果为00，则输出值对应0到0.25之间，直接输出小数部分；如果为01，则输出值对应0.25到0.5之间，对小数部分进行取反加1并输出；如果为10，则输出值对应0.5到0.75之间，直接输出小数部分；如果为11，则输出值对应0.75到1之间，对小数部分进行取反加1并输出；

21、（5）其中，指数与126的差值记为临时指数，会送至临时指数模块。

22、上述方案中，分段拟合系数表中存储的多项式系数为使用c/c++语言数学函数库进行拟合得到的多项式系数，放大指定倍数后再定点化后的值。

23、上述方案中，乘法模块一中使用布斯编码和华莱士树设计的32位×32位乘法器，在进行乘法运算后，得到64位定点结果。

24、上述方案中，移位模块一中右移或左移的位数为：临时指数模块输出的临时指数与系数a放大倍数的和减去系数b放大倍数的差值。

25、上述方案中，移位模块二中右移或左移的位数为：临时指数模块输出的临时指数与系数b放大倍数的和减去系数c放大倍数的差值。

26、一种高精度浮点三角函数的运算方法，采用如上所述的一种高精度浮点三角函数的运算装置，包括如下步骤：

27、（1）浮点数x和三角函数选择信号输入浮点数预处理模块，该模块根据三角函数选择信号过滤非法输入和输入中无需运算的特殊值，将特殊值送至特殊处理模块，由特殊处理模块判断特殊值类型，直接输出对应的函数值；如果输入为非特殊值，则送至定点化模块；

28、（2）定点化模块对浮点数x进行浮点转定点，将转换的定点数发送给分段拟合系数表、乘法模块一和乘法模块二，将转换的临时指数送至临时指数模块进行存储；

29、（3）乘法模块一从分段拟合系数表中获取多项式系数a，进行系数a乘以x的运算，并将定点数积运算结果ax送至移位模块一；

30、（4）移位模块一从临时指数模块获取临时指数，对ax右移或左移指定的位数，使其与b保持相同的放大倍数，并将结果送至加法模块一；

31、（5）加法模块一从分段拟合系数表中获取多项式系数b，并进行ax加b的运算，并将运算结果送至乘法模块二；

32、（6）乘法模块二中进行(ax+b)乘以x的运算，得到的结果送至移位模块二中；

33、（7）移位模块二从临时指数模块获取临时指数，对(ax+b)x结果右移或左移指定的位数，使其与c保持相同的放大倍数，并将结果送至加法模块二；

34、（8）加法模块二从分段拟合系数表中获取多项式系数c，并进行((ax)+b)x+c的运算，结果送至浮点化模块；

35、（9）浮点化模块整形数转换为浮点数后输出浮点数y。

36、通过上述技术方案，本发明提供的一种高精度浮点三角函数的运算装置及方法具有如下有益效果：

37、本发明以一种简单高效的方式实现了三角函数的单精度浮点数计算。该运算装置将输入的浮点数经过处理后转为定点数，通过分段拟合系数表查找对应系数，在运算模块中完成高效的定点计算。临时指数模块和特殊处理模块用于确保数值的准确性和有效性。最终结果通过浮点化模块还原为浮点格式，输出高精度的三角函数值。相比于cordic算法实现的三角函数计算单元缩短了计算时间，更适用于在处理器芯片设计中进行例化实现，提升整体系统性能。