一种基于波浪预测的波浪能转换器控制方法

本发明涉及波浪能发电领域，尤其是涉及一种基于波浪预测的波浪能转换器控制方法。

背景技术：

1、为了跟上全球能源需求的增长，人们开发了各种能源系统，从海洋能源(海上风能、海浪、潮汐等)中提取电力，与其他海洋能源相比，波浪能是一种功率密度高、全天可用的资源，因此，发展利用波浪能被认为是可持续发电的一个极具前景的方案。

2、用于从海浪中获取能量的装置被称为波浪能转换器，虽然目前已经有了一套能量收集理论，但能量收集效率仍然不令人满意，特别是在非谐振状态下。

3、一种被广泛运用的理论是用控制器来调节波浪能转换器的动力学，研究发现最大限度地吸收能量的一个条件是保持波浪速度与波浪激励力相一致。基于此，许多研究人员开始采用离散控制来提高波能转换效率。但是，迄今为止，波浪能转换器控制的研究主要集中在控制策略的制定上，而不在于控制的实际应用，这主要是因为对波浪能转换器的实时控制需要对未来波浪力的准确预测，因此，整个系统的功率捕获能力低下，对波浪能的利用率并不高。

技术实现思路

1、发明目的：针对上述问题，本发明的目的是提供一种基于波浪预测的波浪能转换器控制方法，实现了未来波浪力的准确预测，大大提高波浪能转换器的转换效率。

2、技术方案：一种基于波浪预测的波浪能转换器控制方法，包括以下步骤：

3、s1：建立波浪能转换器的水动力模型；

4、s2：采用多层前馈人工神经网络算法建立波浪力预测模型；

5、s3：以水动力模型的波浪激励力数据作为训练样本，采用深度机器学习算法对多层前馈人工神经网络进行训练，优化波浪力预测模型；

6、s4：通过预测的波浪力，采用非因果模型预测控制算法，对波浪能转换器进行实时分离控制，优化波浪能转换器对随机波中能量的提取效率。

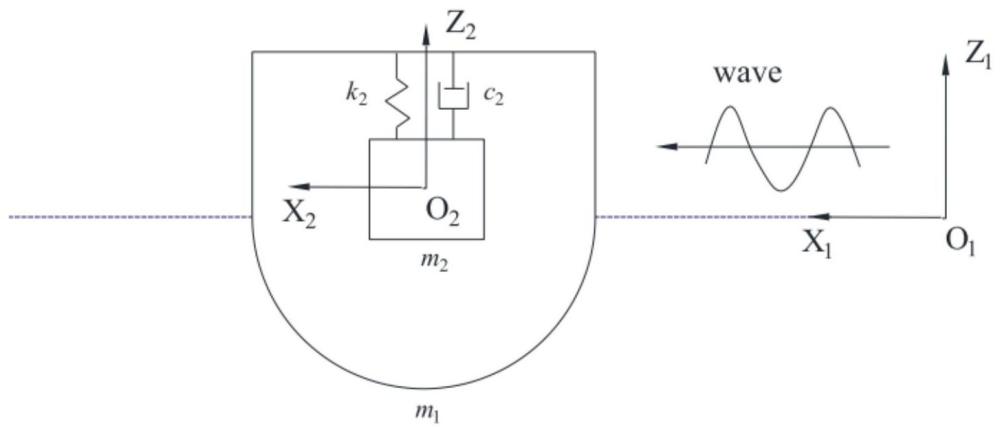
7、进一步的，在步骤s1中，波浪能转换器为双振荡体式波浪能转换器，包括浮子和pto系统，pto系统模拟为线性阻尼器，则双振荡体式波浪能转换器的运动方程为：

8、

9、

10、其中，mi是浮子的质量；μ∞是浮子在无限频率下的水动力附加质量；z，分别是位移，速度和加速度；k1是静水恢复刚度；k2是连接浮子与振荡器的弹簧刚度；d1是浮子粘性载荷的附加线性阻尼；d2是pto系统的阻尼系数；fwave是波浪激励力，h为延迟核函数；

11、最佳的，波浪激励力的公式表达式为：

12、

13、

14、其中，ψ(ωi)为线性波浪激励力的传递函数；s(ω)为jonswap波浪谱；ε是介于[0,2π]之间的随机值，表示不同振荡频率的波分量之间的随机相位差；

15、延迟核函数的公式表达式为：采用边界元分析软件wadam计算波浪激励力、辐射阻尼和附加质量。

16、进一步的，在步骤s2中，采用六层前馈反向传播神经网络构建波浪力预测模型，包括1个输入层、4个隐藏层以及1个输出层，每层的神经元个数为10～12个。

17、最佳的，通过在线测量获取波浪高度作为多层前馈人工神经网络输入样本，在每一个时刻，过去5秒的波浪自由表面高度被输入到一个多层前馈人工神经网络中，以预测未来5秒的波浪力，其中采样率为0.1s，用n个过去波浪高程数据点预测n个未来波浪力数据点，其中n大于或等于50。

18、进一步的，在步骤s3中，对多层前馈人工神经网络的训练为更新和优化权重w和阈值b使预测误差θ最小，预测误差θ公式为：

19、

20、其中，l是学习样例的个数,yk为预测输出，ak为实际值；

21、然后采用梯度下降法和反向传播法对权重w和阈值b进行优化，公式如下：

22、

23、

24、其中，wji'和bji'为一次迭代后的优化参数，κ为学习率，用来表示神经网络在训练过程中学习速度的参数。

25、进一步的，在步骤s4中，对波浪能转换器进行实时分离控制，即根据控制命令β(t)交替接通和断开pto系统，当pto系统加载时，β＝1，当pto系统卸载时，β＝0，加载以及卸载之间的切换通过旁通阀或电子开关完成。

26、最佳的，在步骤s4中，非因果模型预测控制算法模型的建立包括以下步骤：

27、s41：建立波能转换器的五阶状态空间方程：

28、

29、

30、

31、其中，a代表状态矩阵，b代表输入矩阵，c代表输出矩阵；

32、s42：定义状态向量将五阶状态空间方程转换为一阶微分方程：

33、

34、

35、s43：给定初始条件x(0)＝0，利用第四龙格库塔法求解初值，得到波浪能转换器的功率，即目标函数p：

36、

37、s44：结合分离控制的实施，将步骤s42中一阶微分方程进行改写，得到约束方程：

38、

39、

40、s45：引入拉格朗日乘子法，将约束优化问题转化为无约束问题，拉格朗日乘子法的数学表达式为：

41、

42、其中，λ为拉格朗日乘子，h为哈密顿函数，单变量β在0到1之间切换，当β满足：

43、得到拉格朗日乘子法的最优解；

44、其中，为拉格朗日乘子的表达式为：

45、

46、s46：启动β(t)＝0的仿真，对约束方程进行积分，积分区间为时间区间t∈[0,t],获得自由控制动态响应；通过对拉格朗日乘子进行积分，积分区间为时间区间t∈[0,t]，得到拉格朗日乘子λ；基于单变量β，推导出控制命令β(t)，用派生的控制命令重新启动仿真以更新动态响应，迭代过程以优化控制命令，直到收敛。

47、最佳的，对波浪能转换器施加位移约束，每当相对位移z2超过阈值z0时，就施加一个阻尼力来锁定振荡器，带位移约束的波浪能转换器的动力学方程为：

48、

49、

50、

51、考虑到分离控制在一定程度上会导致波浪能转换器偏移幅度的增加，因此对其施加位移约束，本发明采用制动策略对波浪能转换器进行幅值约束，从而进一步优化控制效果。

52、最优分离控制基于人工神经网络预测到的未来波浪力，交替锁定和释放振荡器来调整响应相位，使得浮子的速度和波浪载荷相一致，从而来最大限度地提取波浪能。但是人工神经网络无法预测整个区间[0,t]的未来波浪力。这表明最优分离控制不能直接实现。为了解决这一问题，采用了一种基于模型预测控制策略的改进分离控制，模型预测控制策略在有限的时间区间[ti,ti+δt]上优化控制命令，而不是在整个时间区间[0,t]上优化。因此，在时间区间[ti,ti+δt]上是最优的，但在整个时间区间[0,t]上是次优的。控制命令在更新的时间间隔[ti,ti+δt]的每个时间瞬间进行优化，从而在线实现分离控制。

53、有益效果：与现有技术相比，本发明的优点是：

54、本发明提出了一种基于模型预测控制策略的实时波能控制算法，并将其应用于双振子波能转换装置。为解决波能控制的非因果性，采用人工智能技术，基于自由水面高程对未来波浪力进行在线预测。由于控制算法采用波高而不是波浪谱，因此对波况具有较强的鲁棒性，可以在大范围的海域实施。本发明提出了一种高效的波能技术，大大提高了波能捕获效率，实现了能源成本的显著降低，推动了波浪能转换装置的大规模部署，并最终实现了波能装置对净零目标的潜在贡献。