融合轨迹时空距离和SNN-DPC的出租出行频繁模式挖掘方法

本发明属于轨迹数据挖掘与分析，具体涉及一种融合轨迹时空距离和snn-dpc的出租出行频繁模式挖掘方法。

背景技术：

1、随着现代城市的不断发展和人们生活方式的变化，城市交通系统正日益面临着新的挑战和机遇。在这个快速变革的背景下，如何更好地理解和管理城市中的出行行为成为了一项紧迫的任务。时空轨迹数据，作为记录人类出行活动的珍贵信息源，为我们提供了深入研究城市交通特征和出行模式的机会。作为一种典型的时空轨迹大数据，出租车轨迹数据记录了人类出行的行为活动，携带着丰富的时空关联信息。这些数据在某种程度上能够揭示动态移动车辆背后隐藏的各种特殊事件。出租车轨迹数据的应用广泛涉及多个领域，如频繁路径挖掘、交通拥堵分析、轨迹异常行为检测等。其中，频繁轨迹模式挖掘旨在从海量时空轨迹数据中识别出现频率较高的行程模式，进而揭示出行规律和城市交通的动态变化，引发了广泛的关注和探讨。它的意义不仅在于更好地理解城市交通出行的本质，还在于为城市规划、交通管理、智能交通系统的建设提供了重要的支持。但是，现有的出租出行频繁轨迹模式挖掘算法仍存在抗噪性和识别准确度不佳、时间复杂度高等问题，因此，有必要提出一种新的出租出行频繁模式挖掘方法来解决现有技术存在的问题。

技术实现思路

1、本发明的目的在于提供一种融合轨迹时空距离和snn-dpc的出租出行频繁模式挖掘方法，该方法有利于实现准确、高效的出租出行频繁模式识别。

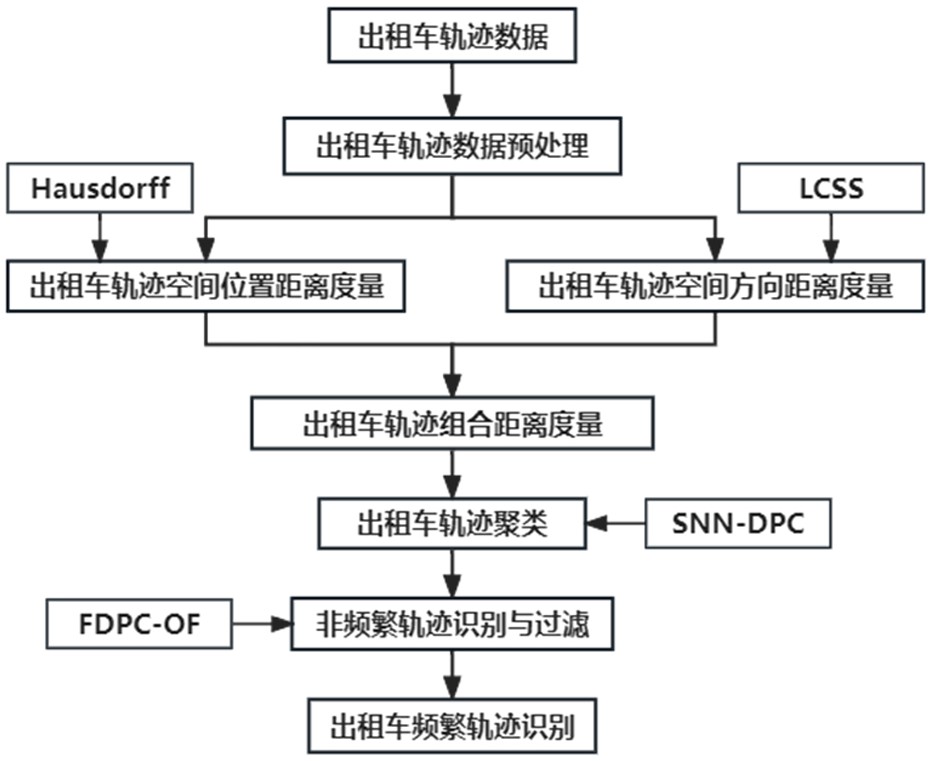
2、为了实现上述目的，本发明采用的技术方案是：一种融合轨迹时空距离和snn-dpc的出租出行频繁模式挖掘方法，包括以下步骤：

3、步骤s1：获取轨迹数据，剔除重复记录和异常的数据并补全缺失数据；

4、步骤s2：对研究区域进行网格化处理，任取不同的2个网格，提取以这两个网格所在区域为起终点的所有轨迹，构建轨迹子数据集；

5、步骤s3：基于改进的hausdorff算法度量轨迹的空间位置相似性，得到轨迹空间位置距离矩阵；

6、步骤s4：基于改进的lcss算法度量轨迹的空间方向相似性，得到轨迹空间方向距离矩阵；

7、步骤s5：将轨迹空间位置距离矩阵和轨迹空间方向距离矩阵进行加权融合，得到轨迹时空距离矩阵；

8、步骤s6：基于snn-dpc算法对处理后的轨迹时空距离矩阵进行聚类分析，将轨迹划分为不同的类簇；

9、步骤s7：基于fdpc-of算法检测聚类结果中的离群轨迹，并予以剔除，最终得到出租出行频繁模式。

10、进一步地，步骤s3具体包括以下步骤：

11、步骤s31：利用轨迹的序列特点，计算数据集中一条轨迹每个轨迹点在整条轨迹中的位置比例信息，然后在另一条轨迹中标记出具有相同位置比例的对应点以及其所在的轨迹段；轨迹点与对应点的关系描述如下：

12、定义pi′为轨迹ta中的一个轨迹点pi在另一条轨迹tb上的一个具有相同位置比例信息的对应点，且pi′满足以下条件：

13、

14、式中，al(p1,pi)为从p1至pi的累积长度，即从轨迹的起始点p1开始累积计算长度直到pi，其中pi′有可能在某一轨迹段上，和分别为两条轨迹的长度；

15、步骤s32：取轨迹点与对应轨迹段起点的距离、轨迹点与对应轨迹段终点的距离以及轨迹点与对应点的距离的最小值，作为该轨迹点至另一条轨迹的距离；计算公式如下：

16、

17、式中，d(i)为当前轨迹中每一个轨迹点pi至另一条轨迹的距离，和分别为轨迹点pi的依位置比例的对应点pi′所在轨迹段的起终点，d(pi,pi′)为两轨迹点间的欧氏距离；

18、步骤s33：计算一条轨迹中所有轨迹点至另一条轨迹的距离，并对其求均值，得到单向hausdorff距离的结果；在两个单向hausdorff距离的度量值中选择最大值，作为轨迹间空间位置相似性距离的最终结果，计算公式如下：

19、h(ta,tb)＝max{h(ta,tb),h(tb,ta)}  (3)

20、其中：

21、

22、式中，h(ta,tb)描述为轨迹ta和轨迹tb的双向hausdorff距离；h(ta,tb)描述为从轨迹ta至轨迹tb的单向hausdorff距离，为轨迹ta的轨迹点数；

23、步骤s34：按步骤s31-s33计算数据集中两两轨迹的空间位置距离，得到轨迹空间位置距离矩阵。

24、进一步地，步骤s4具体包括以下步骤：

25、步骤s41：逐个计算轨迹中相邻轨迹点的坐标差，得到一系列轨迹方向向量；将数据集中的所有轨迹处理成轨迹段方向向量序列，定义如下：

26、

27、

28、式中，lon和lat分别为轨迹点pi的经度和纬度，n为轨迹t中的轨迹点数；

29、步骤s42：设定一个向量夹角阈值θ来判定不同轨迹之间的方向向量是否匹配；

30、步骤s43：构建一个空的二维矩阵，矩阵的大小由两条向量序列的长度决定；

31、步骤s44：从第一条序列的第一个方向向量开始，逐个比较序列中的方向向量与另一条序列中的方向向量，计算它们之间的方向夹角余弦值，并与向量夹角阈值θ的余弦值进行比较，计算出向量相似度，矩阵中各个位置的值由该位置左上角的值与计算出的向量相似度的和、该位置左边位置的值、该位置上方位置的值，这三者中的最大值进行填充，重复该过程，直到填满整个矩阵；计算公式如下：

32、

33、式中，为和向量夹角的余弦值，cos(θ)为向量夹角阈值θ的余弦值；的取值范围在[0,1]，越接近1，表明向量间的相似程度越高；

34、

35、式中，vecseq(i)和vecseq(j)分别为两条轨迹由起始时刻至某一时刻i和j组成的轨迹子序列计算得到的向量子序列；simlcs(vecseq(i),vecseq(j),θ)的值反映两条轨迹可匹配方向向量的相似度之和的最大值；从矩阵的右下角回溯追踪每一个匹配的位置直到左上角，统计其中沿左斜上移动的次数可以得到两条向量序列间的最优匹配子序列长度，记作|lcs(vecseq(i),vecseq(j))|；

36、步骤s45：通过回溯矩阵找到两条轨迹间匹配的最佳的公共子序列以及对应的轨迹方向距离；计算公式如下：

37、

38、式中，和分别为两条向量序列的长度；|lcs(vecseq(i),vecseq(j))|为两条向量序列间的最优匹配子序列长度，考虑其与完整序列长度的比值，比值越大则相似度越高；

39、步骤s46：按步骤s41-s45计算数据集中两两轨迹的空间方向距离，得到轨迹空间方向距离矩阵。

40、进一步地，步骤s5具体包括以下步骤：

41、步骤s51：轨迹间的时空距离由空间位置距离和空间方向距离进行归一化加权得到；计算公式如下：

42、dt(ta,tb)＝wh·h(ta,tb)nor+wl·l(ta,tb)nor  (10)

43、式中，wh和wl分别表示轨迹间距离度量中空间位置距离所占的权重以及空间方向距离所占的权重；h(ta,tb)nor和l(ta,tb)nor分别为归一化后的空间位置距离以及空间方向距离；归一化方法采用最值归一化；

44、步骤s52：加权合并轨迹空间位置距离矩阵和轨迹空间方向距离矩阵，得到轨迹时空距离矩阵。

45、进一步地，步骤s6具体包括以下步骤：

46、步骤s61：计算每一条轨迹在数据集中的局部密度；计算公式如下：

47、

48、其中：

49、

50、式中，|snn(ti,tj)|为轨迹ti和tj的共享近邻数，通过取轨迹ti和tj的k近邻集合的交集个数得到，即knn(ti)∩knn(tj)；k(ti)为与轨迹ti相似度最大的前k条轨迹的集合，相似度由sim(ti,tj)计算得到；

51、步骤s62：计算每一条轨迹在数据集中的相对距离；计算公式如下：

52、

53、如果某条轨迹的局部密度为数据集中的最大值，则其相对距离取所有轨迹相对距离的最大值；

54、步骤s63：计算每条轨迹局部密度和相对距离的乘积，对该值按从大到小进行排序，并根据该值差的变化趋势，自适应选择合适的聚类中心数；计算公式如下：

55、γ＝ρnor·δnor  (14)

56、式中，ρnor和δnor分别为归一化后的局部密度和相对距离值，归一化方法采用最值归一化；

57、scorei＝(i-1)·(γi-γi+1)(i＝1,2,3,...,n)  (15)

58、式中，(i-1)为权值，随着i的增大而增大，降低靠前的几个较大γ差值对聚类中心选取的影响，最后，取scorei最大时，前i个γ所对应的轨迹为自适应选择的聚类中心；

59、步骤s64：依照snn-dpc算法的两步分配策略，依次分配不可避免的从属轨迹以及可能的从属轨迹，为所有轨迹分配一个唯一的类簇标签；计算公式如下：

60、|snn(ta,tb)|≥k/2  (16)

61、0＜|snn(ta,tb)|＜k/2  (17)

62、式中，k为轨迹的最近邻数；如果轨迹ta与轨迹tb的关系满足(16)式，则轨迹tb为轨迹ta的不可避免的从属轨迹，属于同一类；否则满足(17)式，轨迹tb为轨迹ta的可能的从属轨迹，再按原snn-dpc算法中的方式进行判断，决定轨迹tb的类簇分配。

63、进一步地，步骤s7具体包括以下步骤：

64、步骤s71：基于fdpc-of算法中的离群检测算法，分别计算出每一条轨迹的离群因子，并对该值按降序排列，设定一个离群比例，将排名靠前的轨迹识别为离群轨迹并予以过滤，最终得到轨迹的频繁模式挖掘结果；计算公式如下：

65、

66、

67、

68、式中，m为轨迹所属类簇ci的轨迹总条数；davgi为平均向心距离(即类簇ci中所有轨迹与聚类中心的平均距离)；disceni为向心相对距离，即轨迹ti的相对距离与其所属类簇的平均向心距离的比值，fofi为轨迹ti的离群因子，即轨迹ti的向心相对距离与局部密度的比值，如果局部密度为0，则离群因子取无穷大值。

69、与现有技术相比，本发明具有以下有益效果：本发明提供了一种融合轨迹时空距离和snn-dpc的出租出行频繁模式挖掘方法，该方法以snn-dpc算法为基础实现轨迹的聚类过程，并对算法进行改进，以解决聚类中心确定和离群点识别的问题；同时，针对目前部分轨迹度量算法所面临的抗噪性不足、时间复杂度高以及度量准确性不高等问题，从轨迹的空间位置相似性和空间方向相似性两个维度出发，基于改进的hausdorff和lcss实现组合相似性度量，并与snn-dpc算法相结合，以实现更为准确、高效的出租出行频繁模式识别，从而为出租出行轨迹频繁模式挖掘带来更好的解决方案，为实际应用提供更可靠的支持。