基于加速GMRES求解器的自适应扫频电磁仿真方法

本发明属于射频电路工程，涉及一种基于加速gmres(广义最小残差法)求解器的自适应扫频电磁仿真方法。

背景技术：

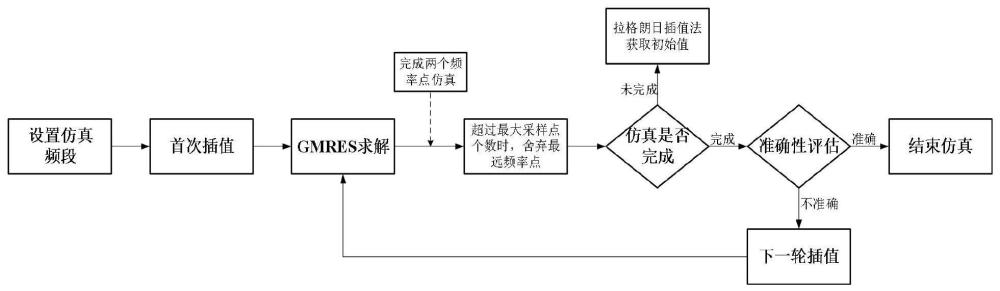
1、随着计算电磁和仿真技术的不断发展，在现在的科学工程任务中，所要求解问题的“电大”尺寸也越来越大，由于复杂“电大”尺寸经过网络剖分形成的未知数量过大，而矩量法下方程组的大小受网络剖分后形成的rwg基函数数量影响，使得形成的方程组规模十分庞大。此时，如果继续选择直接求解方法易受到计算机硬件和资源的限制，在内存资源有限的情况下，将无法存储方程组数据，导致程序崩溃而无法求解方程组。应采用迭代法进行求解，虽然迭代算法能够降低时间复杂度，但由于其初始化电流值与仿真实际电流值差距较大，导致迭代步数过高，从而仿真时间过慢。本发明提出一种基于加速gmres求解器的自适应扫频电磁仿真方法，利用电流在相邻频率点间平滑变化的是思想，预先插值出当前仿真频率点的电流值，预测出的电流值已经在一定程度上接近实际值，有效改善求解器预估电流值误差较大的问题，并与矩量法中的自适应扫频方法相结合，从而提升仿真效率。

技术实现思路

1、本发明的目的是针对现有技术的不足，提供了一种基于加速gmres求解器的自适应扫频电磁仿真方法，计算快、精度高。

2、第一方面，本发明提供一种基于加速gmres求解器的自适应扫频电磁仿真方法，该方法包括以下步骤：

3、步骤(1)、考虑均匀空间中的一个理想导体位于介电常数为ε、磁导率为μ的环境中，在任意一个方向受到入射场的影响，会产生相应的感应电磁流和向外的散射场；假设入射的平面电磁波的入射电场为einc，磁场为hinc，照射到理想导体表面上产生散射电场为esac，散射磁场为hsac，在理想导体内部，内部电场ein和内部磁场hin均为零；

4、步骤(2)、假设仿真频段设定为[f1,fn]，根据二分法插值理论，可知第一轮选取的频率点有三个，分别为f1、fn和fmid，f1为仿真的起始频率点，fn为仿真的结束频率点，fmid为起始和结束频率点的中间值，fmid＝(f1+fn)/2；

5、步骤(3)、对当前选取的频率点采用矩量法求解导体内部电磁场；

6、根据电场积分方程：

7、

8、其中式中表示导体外法向单位矢量，η表示媒质空间的波阻抗，l表示线性算子，j表示电流密度，einc表示入射电场；

9、rwg基函数被定义为在相邻的两个三角形之间具有共同边的情况下，能够模拟任意形状物体表面的电磁流分布；

10、给出rwg基函数的定义式为：

11、

12、其中ln为第n对相邻三角形tn+和公共边的长度，r为三角形上任意的一点，是从三角形tn+的顶点vn+指向点r的矢量，是从三角形的顶点指向点r的矢量，和分别为相邻三角形tn+和的面积；fn(r)表示场区域中第n个rwg基函数；

13、通过使用rwg基函数展开公式(1)中的电流：

14、

15、其中in为待求解的第n个电流展开系数，n为网络剖分后形成的未知数数量；

16、将公式(3)代入公式(1)得到离散后的电场积分方程：

17、

18、其中l(fn(r))表示rwg基函数fn(r)的线性算子方程；

19、采用伽略金法选取rwg基函数作为检验函数，对电场积分方程(4)检验:

20、

21、其中fn(r)表示场区域中第n个rwg基函数；fm(r')表示源区域中点r'第m个rwg基函数；

22、由于rwg基函数沿着表面切向，将公式(5)改写为如下：

23、

24、将公式(6)写为矩阵方程的形式：

25、zi＝v  式(7)

26、其中z为n×n的矩量法阻抗矩阵，v和i为n×1的列向量，分别表示矩量法中的激励向量和电流向量；

27、矩阵z的第m行n列元素、矩阵v的第m行元素表示如下：

28、

29、

30、

31、式中j表示虚数单位，f表示频率点；rwg基函数fm(r')所在的源三角形对为rwg基函数fn(r)所在的场三角形为g(r)为均匀无间空间内的格林函数，r＝|r-r'|表示为从场基函数的任意一个点r到源基函数的任意一个点r'的距离；表示梯度算子，表示散度算子，ds表示场区域面矢量微元，ds'表示源区域面矢量微元；

32、步骤(4)、采用加速gmres(广义最小余参)求解器迭代求解矩阵方程(7)得到仿真频率点的电流值；

33、4-1计算当前频率点的电流值

34、4-1-1对于一个矩阵方程(7)，初始化ii＝i0，i0初始化为0，迭代次数i＝0；

35、4-1-2根据公式(7)可知公式(11)，进而得到残差ri；

36、ri＝v-zii  式(11)

37、4-1-3判断残差ri是否小于人为设定的阈值k时，若是则认为当前频率点的ii即为所求的电流值，否则执行步骤4-1-4；

38、4-1-4将残差ri正交化处理后结果作为初始krylov子空间的基向量，然后进行arnoldi迭代，得到一个近似的解向量ii+1；然后返回至步骤4-1-2，并更新迭代次数i＝i+1；

39、4-2计算第三个频率点的电流值

40、4-2-1根据步骤4-1计算步骤(2)f1、fn和fmid中任意两个频率点的电流值，利用插值算法计算出第三个频率点的预估电流值，将ii初始化为第三个频率点的预估电流值，初始化迭代次数i＝0；

41、4-1-2根据公式(11)，计算得到残差ri；

42、4-1-3判断残差ri是否小于1时，若是则认为当前频率点的预估电流值为有效值，否则将ii重置为0，重复操作步骤4-1-2至4-1-4；

43、步骤(5)、仿真的准确性评估

44、对步骤(2)f1、fn和fmid的电流值结果进行收敛判断，如果满足收敛条件则停止仿真计算，如果不满足收敛条件则利用二分法插值理论进行下一轮增加新的采样频

45、率点，重复步骤(3)-(5)；

46、所述的收敛标准采用误差公式其中s(f)表示频率响应理论值，表示频率响应拟合值；若err＜阈值，即达到收敛，反之则没达到收敛；

47、步骤(6)、根据上述计算得到的电流值即可获知电磁仿真参数，实现电磁仿真。

48、第二方面，本发明提供一种计算机可读存储介质，其上存储有计算机程序，当所述计算机程序在计算机中执行时，令计算机执行所述的方法。

49、第三方面，本发明提供一种计算设备，包括存储器和处理器，所述存储器中存储有可执行代码，所述处理器执行所述可执行代码时，实现所述的方法。

50、本发明基于利用电流平滑变化的特点，将已完成频率点的电流值去预测未开始仿真频率点的电流值，然后把预测得到的值作为初始值，能够有效降低gmres求解器初始电流值与实际电流值差距较大的问题，从而减少后续迭代步数，避免求解器由于初始电流值错误而导致仿真时间慢，同时求解器与矩量法仿真中的自适应扫频方法相结合，能够有效提升仿真效率。