一种基于GA-ACO的移动机器人控制方法及系统

本发明属于机器人控制，具体涉及一种基于ga-aco的移动机器人控制方法及系统。

背景技术：

1、移动机器人是一种常见的移动机器人类型，它们通常使用轮子来移动并执行各种任务。移动机器人的控制方法及系统是确保机器人能够在各种环境中安全、高效地移动和执行任务的关键组成部分。

2、移动机器人属于多变量、非线性、高阶、强耦合、不稳定的基本运动控制系统。目前，对移动机器人控制的算法有很多，如 pid控制、自适应控制、最优控制、智能控制等。基于模糊控制的移动机器人控制系统可以克服系统的不稳定性和非线性性质，但过于依赖专家的经验。而利用线性二次最优控制器( linear quadratic regulator，lqr) 较传统的pid 控制可获得更为稳定的平衡过程，且使系统达到误差跟踪的效果更佳。lqr控制旨在最小化系统状态和控制输入的加权和，以达到最优性能。因此，在符合线性二次最优控制问题的前提下，lqr通常能够提供较好的系统响应和鲁棒性。

3、针对lqr最优控制中存在的参数不确定性问题，最初采用了许多人为参数整定方法。然而，这些方法存在较大的滞后性和随机性，导致控制系统误差增加。近年来，随着传统控制技术与计算机技术的结合，出现了许多新型的控制算法。

4、这些算法可以基于多种智能技术，如蚁群算法、遗传算法、神经网络、人工鱼群算法、免疫算法和粒子群算法等，用于参数调整等目的。这种智能技术的应用使得控制系统更具适应性和灵活性，能够更好地处理参数不确定性的挑战。与传统的人为参数整定方法相比，这些新的组合式控制算法能够提高控制系统的性能，减小误差，并降低操作人员的工作负担。此外，它们还具备更好的实时性，有助于更有效地监测机器人的状态，特别是在移动机器人的控制方面表现更为优越。

5、故此，本技术提出了一种基于ga-aco的移动机器人控制方法及系统。

技术实现思路

1、为了弥补现有技术的不足，以解决背景技术中存在的技术问题，本发明提出了一种基于ga-aco的移动机器人控制方法及系统。

2、本发明通过以下技术方案实现：

3、一种基于ga-aco的移动机器人控制方法，包括以下步骤：

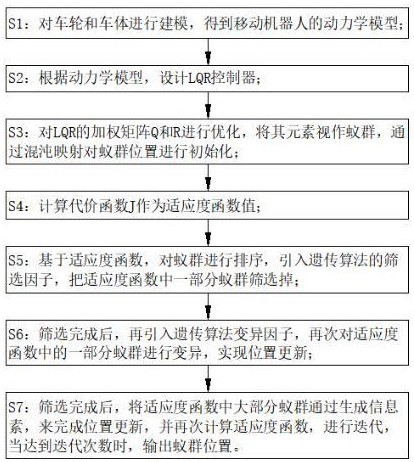
4、s1：对车轮和车体进行建模，得到移动机器人的动力学模型；

5、s2：根据动力学模型，设计lqr控制器；

6、s3：对lqr的加权矩阵q和r进行优化，将其元素视作蚁群，通过混沌映射对蚁群位置进行初始化；

7、s4：计算代价函数j作为适应度函数值；

8、s5：基于适应度函数，对蚁群进行排序，引入遗传算法的筛选因子，把适应度函数中一部分蚁群筛选掉；

9、s6：筛选完成后，再引入遗传算法变异因子，再次对适应度函数中的一部分蚁群进行变异，实现位置更新；

10、s7：筛选完成后，将适应度函数中大部分蚁群通过生成信息素，来完成位置更新，并再次计算适应度函数，进行迭代，当达到迭代次数时，输出蚁群位置。

11、优选的，s1中对于移动机器人的动力学模型的建立包括以下步骤：

12、s11：建立车轮模型；

13、车轮为一对同轴安装，左、右轮相同；其车轮模型由式（1）所得：

14、                                       （1）

15、其中，为车轮的质量，为车轮的半径，为车轮的转动惯量，为车轮水平位移的二阶偏导，为车轮电机输出的扭矩，为车轮从水平方向上对车体施加的作用力；

16、s12：建立车体动力学模型；

17、车体运动包括正向运动和侧向运动；

18、其中，正向运动包括前向运动和绕车体质心n的相对转动；侧向运动包括转向和偏航；

19、车体水平方向方程由式（2）所得：

20、                                    （2）

21、上式中，为车体的质量，为左右两车轮之间的轮距，为质心n距底盘中心o的距离，为车体与竖直方向所成的夹角，为车体所用的时间，和分别为右轮和左轮对车体竖直方向上的支撑力；

22、车体刚体转动方程由式（3）所得：

23、  （3）

24、上式中，为车体绕质心转动时的转动惯量,为车体与竖直方向所成夹角的二阶偏导，和分别为右轮和左轮对车体竖直方向上的支撑力，为右车轮从水平方向上对车体施加的作用力，为左车轮从水平方向上对车体施加的作用力，为右车轮电机输出的扭矩，为左车轮电机输出的扭矩；

25、车体进转向方程由式（4）所得：

26、                                        （4）

27、上式中，为左右两车轮之间的轮距，为车体绕竖直方向转动时的转动惯量，为车体的偏航角；

28、当左右两轮转动速度不等时，车体转向。

29、优选的，s2中具体包括以下步骤：

30、s21：基于移动机器人的车轮模型、车体模型，构建控制系统的状态空间方程；

31、s22：设计状态反馈控制器由式（5）对系统性能进行控制，并对于系统性能引入代价函数由式（6）；

32、                                              （5）

33、                                  （6）

34、上式（5）中，为表示信号，为表示状态，由式（7）所得；

35、上式（6）中，q为维半正定的状态加权矩阵，r为维半正定的控制加权矩阵；q和r式对称矩阵且常取对角阵；q中对角线上的元素qi表示对相应误差分量xi的重视程度，为状态的转置矩阵；为信号的转置矩阵；

36、                                           （7）

37、上式中，s为黎卡提方程的解，为计算值的转置矩阵。

38、优选的，s3中生成蚁群初始位置的logistic映射方程由式（8）所得：

39、                      （8）

40、上式中，为第i组蚁群第j只蚂蚁初始时刻的位置，i取0到m的整数，m为当前蚁群总组数，j取1到8的整数；λ为分叉参数；rand为随机函数，生成0到1的随机数；和为值的上下限，分别取为99和0。

41、优选的，s4中适应度函数由式（9）所得：

42、                       （9）

43、上式中，加权矩阵q中的对角线元素为蚁群中的q1，q2，q3，q4，q5，q6，加权矩阵r的对角线元素为蚁群中的q7，q8，为第i组蚁群的适应度函数。

44、优选的，s6中引入变异因子为0.1，对其中适应度函数最大的10%的蚁群进行变异，对其中每组蚁群中的元素进行二进制编码，转化为一个7位的二进制序列，由概率公式式（10）所得：

45、                                            （10）

46、式中，n为需要进行变异的蚁群组数，n=m*η；

47、变异完成后，再转换为十进制，实现变异蚁群的位置更新。

48、优选的，s7中每组蚁群根据路径上残留的信息素和启发式信息来选择下一个位置，其概率由式（11）所得：

49、                         （11）

50、式中，为t时刻蚁群位置i到蚁群位置j的信息素强度，为能见度，是蚁群位置i和蚁群位置j之间几何距离的倒数，几何距离表达式由式（12）所得：

51、                              （12）

52、为两常数，分别为信息素和能见度的加权值，为尚未更新过的蚁群位置集合；

53、当蚁群完成一次位置更新后，路径上的信息素也随之更新由式（13）所得：

54、                   （13）

55、式中，为信息素挥发度，取0.5，增大可以使算法尝试新的解，减小则使得继续优化当前解，由式（14）所得：

56、         （14）

57、表示本次迭代中路径ij上信息素的增量，基于排序的蚁群信息素生成方法为，蚂蚁按旅行距离排名，蚂蚁释放的信息素的量要和蚂蚁的排名相乘，排名前z-1位的蚂蚁和精英蚂蚁释放信息素，排名第k位的蚂蚁乘以系数z-k，由式（15）所得：

58、                       （15）

59、式中，表示第k组蚁群在迭代中留在路径ij上的信息素的增量；

60、；

61、；

62、生成完信息素后，基于概率公式式（16）进行位置更新：

63、（16）

64、基于更新后的适应度函数，来选择是否更新，适应度函数更小，则进行更新，反之则不；更新后的值如果超出区间范围，则取对应的上下限，超出上限取最大值，超出下限取最小值。

65、一种基于ga-aco的移动机器人系统，包括：

66、建模模块，所述建模模块用于对车轮和车体进行建模；

67、设计模块，所述设计模块用于根据建模模块所设计的模型进行lqr控制器的设计；

68、优化模块，所述优化模块用于对lqr控制器进行优化；

69、计算模块，所述计算模块用于计算代价函数j；

70、筛选模块，所述筛选模块用于对蚁群进行排序筛选；

71、调整模块，所述调整模块用于实现对位置进行更新并得到最优位置。

72、本发明的有益效果是：

73、本发明在机器人控制方法上，采用现代控制理论的lqr控制，较传统的pid控制可获得更为稳定的平衡过程，且使系统达到误差跟踪的效果更佳；且针对lqr最优控制中存在的参数不确定性问题，较人为参数整定方法，通过计算机算法来选取和优化参数，降低滞后性，随机性和控制系统的误差，融合了遗传算法和蚁群算法，避免了单一算法易陷入局部最优的问题。