一种基于最优弹道的复合制导律设计方法

本发明属于飞行器制导，具体涉及一种基于最优弹道的复合制导律设计方法。

背景技术：

1、滑翔飞行器是一种由飞机装载、可在多种高度和速度条件下投放的、进行亚声速和跨声速飞行的空对地精确制导飞行器，具有价格低廉、与载机相容性好等优点。由于滑翔飞行器大空域、宽速域投放使用的特点，最大射程作为该类飞行器在设计中的重点关注。飞行性能分析中的最大射程分析常采用轨迹优化方法，通过设计最优弹道进行求解。为提高最大射程的分析精度，在提高轨迹优化精度的同时，还需研究最大射程的具体实现问题。

2、通过求解轨迹优化问题进行最优弹道设计，可得到滑翔飞行器给定投放条件下的最优射程。该方法不受具体导引方式影响，能评估滑翔飞行器本身的设计效果，却存在评估射程较难实现的问题。因为轨迹优化得到的控制指令是开环的，不能根据飞行器实际状态进行调整，如实际状态与优化结果存在偏差，则需重新进行优化，而实时求解最优轨迹尚存难度，且出于问题复杂度和求解效率考虑，用于轨迹优化的模型一般存在大量简化，导致优化结果的精度和可实现性存疑。除基于轨迹优化的方式外，滑翔飞行器最优射程的评估还可通过设计制导律的方法进行。设计制导律并进行弹道仿真，能够综合考虑动态特性、制导、控制和测量执行机构等因素的影响，得到的最优射程具有更高的精度和可信度。然而，受具体导引方式影响，该类方法分析结果的最优性较差。

3、在此基础上，如能参考最优弹道，通过一定的数值算法，设计制导律实现最优射程，一方面可以进一步验证轨迹优化结果的精度和可实现性，另一方面则缓解了制导律方法分析结果最优性较差的问题。

技术实现思路

1、有鉴于此，本发明的目的在于提出了一种基于最优弹道的复合制导律设计方法，能够满足滑翔飞行器最远射程制导律的设计需求，且兼顾射程和弹道终端约束，最终射程接近最优弹道射程。

2、为达到上述目的，本发明提供如下技术方案：

3、本发明所提供的一种基于最优弹道的复合制导律设计方法，包括：

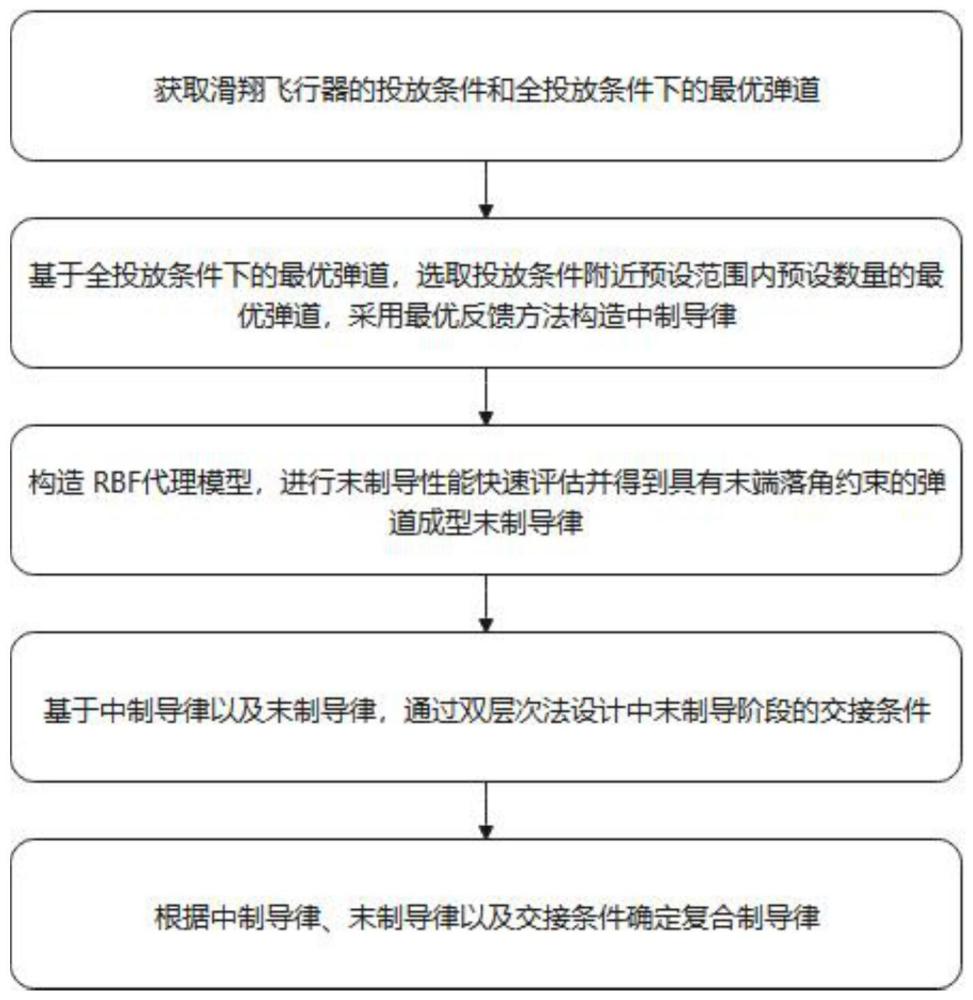
4、获取滑翔飞行器的投放条件和全投放条件下的最优弹道；

5、基于全投放条件下的最优弹道，选取投放条件附近预设范围内预设数量的最优弹道，采用最优反馈方法构造中制导律；

6、构造rbf代理模型，进行末制导性能快速评估并得到具有末端落角约束的弹道成型末制导律；

7、基于中制导律以及末制导律，通过双层次法设计中末制导阶段的交接条件；

8、根据中制导律、末制导律以及交接条件确定复合制导律。

9、优选的，全投放条件下的最优弹道通过以下方式得到：

10、确定滑翔飞行器的投放条件，通过自适应legendre-gauss-radau配点法进行轨迹优化，得到的最优射程弹道；

11、以最优射程弹道的指令俯仰角为控制指令，采用弹道仿真程序进行开环弹道仿真，得到相同初始投放条件下的弹道仿真结果；

12、根据弹道仿真结果以切比雪夫距离最近为度量，进行最优弹道的选取，得到特定投放条件下的最优弹道；

13、基于多个特定投放条件下的最优弹道统计得到全投放条件下的最优弹道。

14、优选的，选取投放条件附近预设范围内预设数量的最优弹道包括：

15、采用最优拉丁超方算法在初始投放条件的扰动空间内进行均匀采样，获得预设数量的采样结果；

16、以采样结果为初始投放条件，调用自适应legendre-gauss-radau配点法进行轨迹优化，得到预设数量的最优弹道。

17、优选的，基于最优反馈方式构造的中制导律的形式为：

18、

19、其中，为俯仰角指令，h为飞行高度，ma为飞行马赫数，θ为飞行器当前的弹道倾角，surrogate(·)为拟合的最优反馈控制器代理模型。

20、优选的，最优反馈控制器代理模型通过以下方式得到：

21、提取样本最优弹道的轨迹优化节点处的状态量为样本点，对应的俯仰角指令为响应值；

22、以样本点状态的最大值为参考量对所有状态量进行归一化处理，得到用于拟合最优反馈控制器代理模型的样本点集；

23、选取样本点集中样本点和对应的响应值为输入，采用rbf方法构造以状态为输入，俯仰角控制指令为输出的最优反馈控制器代理模型。

24、优选的，构造rbf代理模型，进行末制导性能快速评估并得到具有末端落角约束的弹道成型末制导律包括：

25、采用最优拉丁超方采样，在给定的设计变量取值范围中均匀选取预设个数的样本点并确定对应的末制导段弹道仿真初始条件；其中，初始条件根据弹目距离和弹道高度两个设计变量，通过对中制导段实际制导轨迹中弹道高度、速度和弹道倾角数据的插值得到；

26、采用蒙特卡洛方法对每个初始条件分别进行预设次数的蒙特卡洛仿真，获取其中的弹道终端马赫数的最小值；

27、采用一阶多项式作为全局近似模型，多二次函数作为径向函数，以弹道终端马赫数最小值为响应值，构造rbf模型，形成末制导快速评估模型；

28、通过末制导快速评估模型进行末制导性能快速评估并得到具有末端落角约束的弹道成型末制导律。

29、优选的，具有末端落角约束的弹道成型末制导律的导引规律为：

30、

31、其中，为末制导律对应的末制导项，v表示飞行器的速度，kqd和kqd1为比例导引项和视线角约束项的权重系数，qd和分别表示飞行器和目标点之间的视线角和视线角速度，θdf为要求的弹道终端落角，r表示飞行器与目标点之间的距离。

32、优选的，基于中制导律以及末制导律，通过双层次法设计中末制导阶段的交接条件包括：

33、以遗传算法为优化器，交接点的弹目距离和弹道高度为设计变量，在满足弹道终端约束的条件下进行复合制导律交接条件设计；

34、在设计过程当中采用双层次法，其中，第一层次为中制导段，以最大射程为目标进行优化，第二层次为末制导段，构造末制导段经过蒙特卡洛方法分析的各种误差下最小末速的代理模型，以遗传算法为优化器形成末制导段快速评估模型参与交接条件的设计优化；

35、其中，通过对得到的中制导段轨迹插值，得到全部交接条件信息，并采用末制导快速评估模型获取的射程作为目标函数，弹道终端的马赫数最小值作为约束对交接条件进行优化。

36、优选的，交接条件采用线性交接规律，其形式表示为：

37、

38、其中，rgoin和rgoout为弹道的设计变量，本文将rgoout设为常值，取(rgoin-500)，从rgoin到rgoout为变化时，中制导项指令的比重线性减小，末制导项和加速度偏置项指令的比重线性增加，通过这样的变化，中制导项侧重提高滑翔飞行器的射程，末制导项保证弹道终端约束的满足，krgo为随剩余飞行距离(rgo)变化的权重项。

39、优选的，复合制导律的形式为：

40、

41、其中，atraj表示弹道坐标系下的复合制导律，krgo为随剩余飞行距离(rgo)变化的权重项，为中制导律对应的中制导项，为末制导律对应的末制导项，为加速度偏置项。

42、本发明至少取得了以下有益效果：

43、1.本发明克服现有技术不足，提出一种基于最优弹道的复合制导律设计方法，能够满足滑翔飞行器飞行性能中最远射程制导律的设计需求，设计的制导律对状态误差具有良好的适应性，能够兼顾射程和弹道终端约束，最终射程接近最优弹道射程，缓解了制导律方法分析结果最优性较差的问题。

44、本发明的其他优点、目标和特征将在随后的说明书中进行阐述，并且在某种程度上对本领域技术人员而言是显而易见的，或者本领域技术人员可以从本发明的实践中得到教导。本发明的目标和其他优点可以通过下面的说明书来实现和获得。