复杂曲面五自由度平底刀端铣刀路优化方法及系统

本发明涉及数控加工制造，具体地，涉及一种复杂曲面五自由度平底刀端铣刀路优化方法及系统。

背景技术：

1、五轴数控铣床被广泛应用于诸如叶轮、螺旋桨、涡轮叶片等复杂曲面类零件的加工。平底刀端铣在五轴数控加工中是常用的铣削方法，通过调整刀具姿态，平底刀端铣相比于传统球头刀，可以有效增大刀具的加工切宽，提高材料去除率，提高加工效率。

2、目前针对球头刀端铣的刀路生成方法，通常将切触线路径优化和刀轴姿态优化分步、独立进行，但这一框架很难拓展到平底刀端铣加工中。由于平底刀的进给方向和刀轴姿态对刀具与曲面间的切触关系同时有影响，使得切触线路径和刀轴姿态的分步优化无法获得最优的刀位。同时，五轴机床运动学的非线性使得在刀路优化中，除了要考虑切宽，还需要考虑各轴关节路径的光顺性以提高加工效率。现有的刀路优化方法，要么没有做到切触线路径和刀轴姿态的同步优化，要么没有同时考虑切宽和关节路径光顺性，要么使用了效率较低的启发式算法。

技术实现思路

1、针对现有技术中的缺陷，本发明的目的是提供一种复杂曲面五自由度平底刀端铣刀路优化方法及系统。

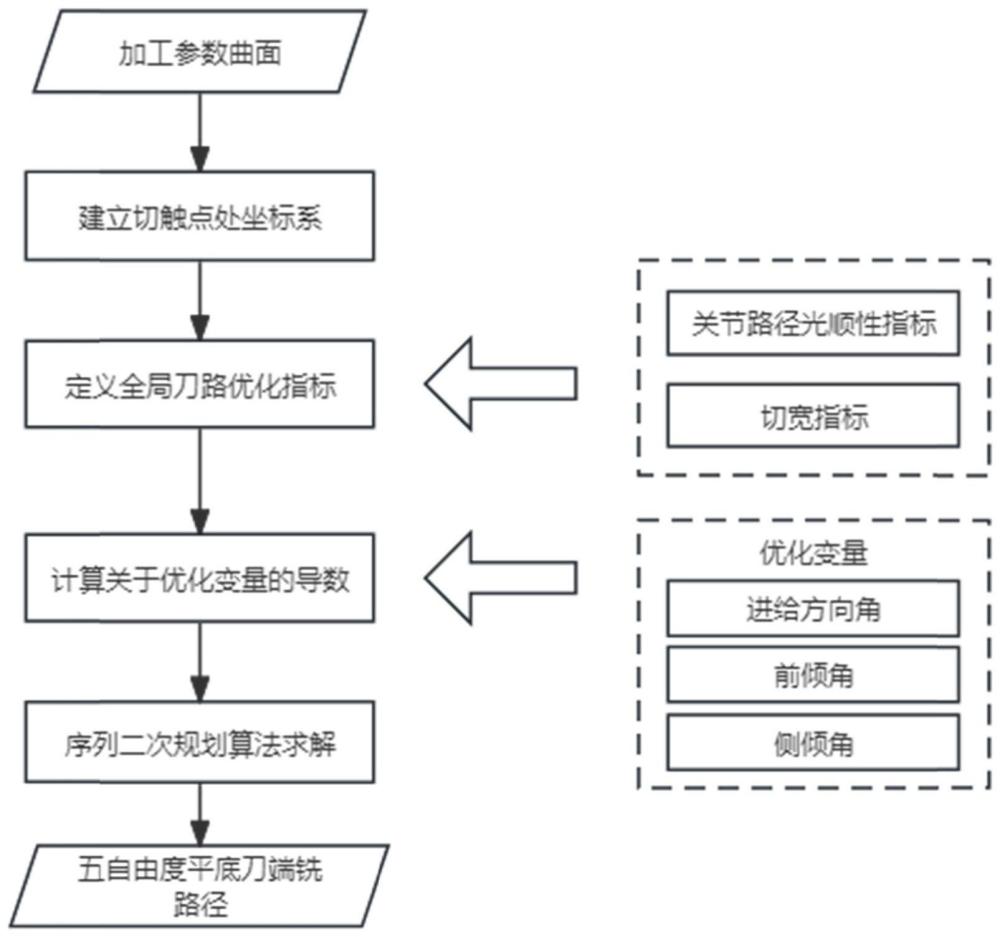
2、根据本发明提供的一种复杂曲面五自由度平底刀端铣刀路优化方法，包括：

3、步骤s1：读取加工参数曲面信息；

4、步骤s2：读取初始刀路信息，计算刀具与加工曲面的离散切触点以及刀具的进给方向角、前倾角、侧倾角，在每个切触点处建立主曲率坐标系、局部坐标系和刀具坐标系；

5、步骤s3：建立全局刀路优化指标，优化指标同时包括各轴关节路径光顺性和切宽；

6、步骤s4：以平底刀在切触点处的进给方向角、前倾角、侧倾角为优化标量，以全局刀路优化指标最小化为优化目标，以各轴限位、避免加工曲面与刀具的干涉为约束，建立优化模型；

7、步骤s5：计算优化目标函数关于优化变量的导数，采用序列二次规划算法求解优化模型；

8、步骤s6：根据优化结果生成平底刀端铣的离散刀位点或连续刀路。

9、优选地，在所述步骤s2中：

10、读取初始刀路信息，包括起始切触点、初始进给方向、步距；记刀位序号为i∈{1,…,n}，由当前切触点cci和该点处进给方向fi计算下一个切触点cci+1的公式为：

11、cci+1＝s(ui+δui,vi+δvi)≈s(ui,vi)+suδui+svδvi＝cci+fiδsi

12、其中，s(u,v)为加工曲面，ui,vi为曲面s在第i个切触点cci处对应的曲纹坐标，δui,δvi为曲面s在第i个切触点cci处对应的曲纹坐标增量，为曲面关于其曲纹坐标的一阶导，δsi为给定步距；

13、在各切触点处建立如下坐标系：

14、主曲率坐标系{l1,l2,n；cc}，其中cc为曲面切触点，l1,l2为曲面在切触点cc处的主曲率方向，n为曲面在切触点cc处的法方向；

15、局部坐标系{f,b,n；cc}，其中f为进给方向，n为曲面在切触点cc处的法方向，b＝n×f为进给垂直方向，f和l1之间的夹角为进给方向角θ；

16、刀具坐标系{xt,yt,o；p}，令初始侧倾角ω＝0，在当前进给方向角和侧倾角条件下，计算无干涉的最小前倾角λ为初始前倾角，由运动学关系进一步建立刀具坐标系，刀具坐标系的原点为刀尖点p，x轴为xt，y轴为yt，z轴为刀轴方向o。

17、优选地，在所述步骤s3中：

18、建立全局刀路优化指标的具体方法为：

19、基于所述的n个刀位，通过逆运动学求得各个刀位对应的各轴关节位置q，使用数值差分公式，获取关节位置关于刀尖点路径弧长参数的一阶导数与二阶导数，建立全局关节路径光顺性指标：

20、

21、其中，dsi表示第i个切触点位置与第i+1个切触点位置之间的差分距离，表示第i个刀位对应的第j个关节位置关于切触路径弧长参数的一阶导数，表示第i个刀位对应的第j个关节位置关于切触路径弧长参数的二阶导数，k1与k2分别为权重值；

22、基于所述的n个刀位，计算第i个刀位处平底刀刀具底圆与残高偏置曲面的两个交点pa，pb，pa，pb满足

23、||pa-qa||＝h，||pb-qb||＝h

24、

25、其中，qa，qb分别为pa，pb到曲面的投影点，为曲面投影点处的切空间，h为给定的残高误差；

26、记刀具坐标系中的x轴xt到向量的有向角度为α，到向量的有向角度为β，其中α＞0，β＜0，计算第i个切触点处的切宽wi：

27、wi＝(pa-pb)·bi＝r(sinα-sinβ)cosωi+r(cosα-cosβ)sinωicosλi

28、其中，r为平底刀刀具半径，bi为切触点cci处的进给垂直方向，λi，ωi分别为切触点cci处的前倾角、侧倾角，建立全局切宽指标：

29、

30、其中，kw为权重值；

31、建立全局刀路优化指标：

32、φ＝φsmooth+φwidth

33、优选地，在所述步骤s4中：

34、建立全局刀路优化模型的具体方法为：

35、将全局刀路优化指标进一步放缩，生成最终的优化指标，以最小化该指标为优化目标，以平底刀在切触点处的进给方向角、前倾角、侧倾角为优化标量，以各轴限位、避免加工曲面与刀具的干涉为约束，建立优化模型：

36、

37、s.t.ψ≥-wi

38、qmin≤qi≤qmax

39、ωmin≤ωi≤ωmax

40、θmin≤θi≤θmax

41、

42、其中，n为刀位点的个数，x＝[θ1,λ1,ω1,…,θn,λn,ωn]为各个刀位处的前倾角、侧倾角、进给方向角构成的向量，x和放缩引入的变量ψ为优化变量；θi,λi,ωi分别为每个切触点处的进给方向角、前倾角、侧倾角；qi为每个切触点处的关节变量，通过机床逆运动学求解；qmin,qmax分别为关节的最小、最大限位；θmin,θmax分别为进给方向角的最小、最大限位；ωmin,ωmax分别为侧倾角的最小、最大限位；fλ(x)为求解刀具无干涉前倾角下限的函数。

43、优选地，在所述步骤s5中：

44、计算优化目标函数关于优化变量的导数的具体方法为：

45、记刀位序号为i∈{1,…,n},计算各个切触点cci处主曲率方向l1i,l2i关于一阶导sui,svi的分量，记为l1i＝asui+bsvi,l2＝csui+dsvi，其中a,b,c,d为系数；切触点cci处进给方向fi关于sui,svi的分量为：

46、fi＝cos(θi)l1i+sin(θi)l2i＝[a cos(θi)+c sin(θi)]sui+[b cos(θi)+d sin(θi)]svi

47、其中，θi为切触点cci处的进给方向角，系数a,b,c,d的计算公式如下：

48、

49、

50、其中，e,f,g为曲面的第一基本形式，κ1,κ2为曲面的主曲率，为主曲率κ1对应的切方向，表示主曲率κ2对应的切方向，l,m,n为曲面的第二基本形式，系数a,b,c,d为关于曲面第一基本形式e,f,g、第二基本形式l,m,n的函数；

51、对于刀位序号i∈{1，…，n}，计算第i个切触点处曲纹坐标ui，vi关于第j个进给方向角θj的导数，由(ui+1，vi+1)＝(ui+δui，vi+δvi)，得导数的计算公式：

52、

53、其中，δui，δvi为曲纹坐标增量，计算δui，δvi的公式为δui＝[a cos(θi)+csin(θi)]δsi，δvi＝[b cos(θi)+d sin(θi)]δsi，a，b，c，d为系数，δsi为给定步距；计算曲纹坐标增量δui，δvi关于第j个进给方向角θj的导数需计算系数a，b，c，d关于θj的导数需计算曲面第一基本形式e，f，g、第二基本形式l，m，n关于θj的导数，加工曲面s的一阶导su，sv、二阶导suu，suv，svv关于θj的导数，整个过程迭代求解，当有了的值后，计算

54、计算切触点处主曲率坐标系{l1，l2，n；cc}，以及刀尖点位置p和刀轴姿态o关于优化变量[θ1，λ1，ω1，…，θn，λn，ωn]的导数；

55、根据微分运动学，计算切触点处关节变量q关于优化变量[θ1，λ1，ω1，…，θn，λn，ωn]的导数；

56、计算各个切触点处切宽wi关于优化变量[θ1，λ1，ω1，…，θn，λn，ωn]的导数；交点pa或pb为平底刀刀具底圆上的点，由主曲率坐标系{l1，l2，n；cc}，刀具前倾角λ、侧倾角ω、进给方向角θ，有向角度α，β表示；交点pa的微分位于其曲面投影点qa处的切空间，满足其中为曲面在pa的投影点qa处的法向量；交点pb的微分位于其曲面投影点qb处的切空间，满足其中为曲面在pb的投影点qb处的法向量，下述公式成立：

57、

58、

59、有向角度α,β的微分转化为关于前倾角λ，侧倾角ω，进给方向角θ1,θ2,…,θn的微分，得到切宽wi关于前倾角λ，侧倾角ω，进给方向角θ1,θ2,…,θn的导数；

60、使用序列二次规划求解优化问题，对于第k次迭代，优化变量的当前值为xk,ψk，求解xk,ψk附近的二次规划子问题，子问题的优化变量为增量δx,δψ

61、

62、

63、

64、ωmin≤ωik+δωi≤ωmax

65、θmin≤θik+δθi≤θmax

66、

67、其中，θik,λik,ωik为刀具在第i个切触点处第k次迭代时的进给方向角、前倾角、侧倾角；qi为每个切触点处的关节变量，qmin,qmax分别为关节的最小、最大限位，θmin,θmax分别为进给方向角的最小、最大限位，ωmin,ωmax分别为侧倾角的最小、最大限位，fλ(x)为求解刀具无干涉前倾角下限的函数；

68、二次规划子问题中的矩阵h和向量f通过下列公式计算：

69、

70、

71、其中，dsi为第i个切触点位置与第i+1个切触点位置之间的差分距离，为第i个刀位对应的第j个关节位置关于切触路径弧长参数的一阶导数，为第i个刀位对应的第j个关节位置关于切触路径弧长参数的二阶导数，k1,k2为权重值。

72、根据本发明提供的一种复杂曲面五自由度平底刀端铣刀路优化系统，包括：

73、模块m1：读取加工参数曲面信息；

74、模块m2：读取初始刀路信息，计算刀具与加工曲面的离散切触点以及刀具的进给方向角、前倾角、侧倾角，在每个切触点处建立主曲率坐标系、局部坐标系和刀具坐标系；

75、模块m3：建立全局刀路优化指标，优化指标同时包括各轴关节路径光顺性和切宽；

76、模块m4：以平底刀在切触点处的进给方向角、前倾角、侧倾角为优化标量，以全局刀路优化指标最小化为优化目标，以各轴限位、避免加工曲面与刀具的干涉为约束，建立优化模型；

77、模块m5：计算优化目标函数关于优化变量的导数，采用序列二次规划算法求解优化模型；

78、模块m6：根据优化结果生成平底刀端铣的离散刀位点或连续刀路。

79、优选地，在所述模块m2中：

80、读取初始刀路信息，包括起始切触点、初始进给方向、步距；记刀位序号为i∈{1,…,n}，由当前切触点cci和该点处进给方向fi计算下一个切触点cci+1的公式为：

81、cci+1＝s(ui+δui,vi+δvi)≈s(ui,vi)+suδui+svδvi＝cci+fiδsi

82、其中，s(u,v)为加工曲面，ui,vi为曲面s在第i个切触点cci处对应的曲纹坐标，δui,δvi为曲面s在第i个切触点cci处对应的曲纹坐标增量，为曲面关于其曲纹坐标的一阶导，δsi为给定步距；

83、在各切触点处建立如下坐标系：

84、主曲率坐标系{l1,l2,n；cc}，其中cc为曲面切触点，l1,l2为曲面在切触点cc处的主曲率方向，n为曲面在切触点cc处的法方向；

85、局部坐标系{f,b,n；cc}，其中f为进给方向，n为曲面在切触点cc处的法方向，b＝n×f为进给垂直方向，f和l1之间的夹角为进给方向角θ；

86、刀具坐标系{xt,yt,o；p}，令初始侧倾角ω＝0，在当前进给方向角和侧倾角条件下，计算无干涉的最小前倾角λ为初始前倾角，由运动学关系进一步建立刀具坐标系，刀具坐标系的原点为刀尖点p，x轴为xt，y轴为yt，z轴为刀轴方向o。

87、优选地，在所述模块m3中：

88、建立全局刀路优化指标的具体方法为：

89、基于所述的n个刀位，通过逆运动学求得各个刀位对应的各轴关节位置q，使用数值差分公式，获取关节位置关于刀尖点路径弧长参数的一阶导数与二阶导数，建立全局关节路径光顺性指标：

90、

91、其中，dsi表示第i个切触点位置与第i+1个切触点位置之间的差分距离，表示第i个刀位对应的第j个关节位置关于切触路径弧长参数的一阶导数，表示第i个刀位对应的第j个关节位置关于切触路径弧长参数的二阶导数，k1与k2分别为权重值；

92、基于所述的n个刀位，计算第i个刀位处平底刀刀具底圆与残高偏置曲面的两个交点pa，pb，pa，pb满足

93、||pa-qa||＝h，||pb-qb||＝h

94、

95、其中，qa，qb分别为pa，pb到曲面的投影点，为曲面投影点处的切空间，h为给定的残高误差；

96、记刀具坐标系中的x轴xt到向量的有向角度为α，到向量的有向角度为β，其中α＞0，β＜0，计算第i个切触点处的切宽wi：

97、wi＝(pa-pb)·bi＝r(sinα-sinβ)cosωi+r(cosα-cosβ)sinωicosλi

98、其中，r为平底刀刀具半径，bi为切触点cci处的进给垂直方向，λi，ωi分别为切触点cci处的前倾角、侧倾角，建立全局切宽指标：

99、

100、其中，kw为权重值；

101、建立全局刀路优化指标：

102、φ＝φsmooth+φwidth

103、优选地，在所述模块m4中：

104、建立全局刀路优化模型的具体方法为：

105、将全局刀路优化指标进一步放缩，生成最终的优化指标，以最小化该指标为优化目标，以平底刀在切触点处的进给方向角、前倾角、侧倾角为优化标量，以各轴限位、避免加工曲面与刀具的干涉为约束，建立优化模型：

106、

107、s.t.ψ≥-wi

108、qmin≤qi≤qmax

109、ωmin≤ωi≤ωmax

110、θmin≤θi≤θmax

111、

112、其中，n为刀位点的个数，x＝[θ1,λ1,ω1,…,θn,λn,ωn]为各个刀位处的前倾角、侧倾角、进给方向角构成的向量，x和放缩引入的变量ψ为优化变量；θi,λi,ωi分别为每个切触点处的进给方向角、前倾角、侧倾角；qi为每个切触点处的关节变量，通过机床逆运动学求解；qmin,qmax分别为关节的最小、最大限位；θmin,θmax分别为进给方向角的最小、最大限位；ωmin,ωmax分别为侧倾角的最小、最大限位；fλ(x)为求解刀具无干涉前倾角下限的函数。

113、优选地，在所述模块m5中：

114、计算优化目标函数关于优化变量的导数的具体方法为：

115、记刀位序号为i∈{1,…,n},计算各个切触点cci处主曲率方向l1i,l2i关于一阶导sui,svi的分量，记为l1i＝asui+bsvi,l2＝csui+dsvi，其中a,b,c,d为系数；切触点cci处进给方向fi关于sui,svi的分量为：

116、fi＝cos(θi)l1i+sin(θi)l2i＝[a cos(θi)+c sin(θi)]sui+[b cos(θi)+d sin(θi)]svi

117、其中，θi为切触点cci处的进给方向角，系数a,b,c,d的计算公式如下：

118、

119、

120、其中，e,f,g为曲面的第一基本形式，κ1,κ2为曲面的主曲率，为主曲率κ1对应的切方向，表示主曲率κ2对应的切方向，l,m,n为曲面的第二基本形式，系数a,b,c,d为关于曲面第一基本形式e,f,g、第二基本形式l,m,n的函数；

121、对于刀位序号i∈{1,…,n}，计算第i个切触点处曲纹坐标ui,vi关于第j个进给方向角θj的导数，由(ui+1,vi+1)＝(ui+δui,vi+δvi)，得导数的计算公式：

122、

123、其中，δui,δvi为曲纹坐标增量，计算δui,δvi的公式为δui＝[a cos(θi)+csin(θi)]δsi，δvi＝[b cos(θi)+d sin(θi)]δsi，a,b,c,d为系数，δsi为给定步距；计算曲纹坐标增量δui,δvi关于第j个进给方向角θj的导数需计算系数a,b,c,d关于θj的导数需计算曲面第一基本形式e,f,g、第二基本形式l,m,n关于θj的导数，加工曲面s的一阶导su,sv、二阶导suu,suv,svv关于θj的导数，整个过程迭代求解，当有了的值后，计算

124、计算切触点处主曲率坐标系{l1,l2,n；cc}，以及刀尖点位置p和刀轴姿态o关于优化变量[θ1,λ1,ω1,…,θn,λn,ωn]的导数；

125、根据微分运动学，计算切触点处关节变量q关于优化变量[θ1,λ1,ω1,…,θn,λn,ωn]的导数；

126、计算各个切触点处切宽wi关于优化变量[θ1,λ1,ω1,…,θn,λn,ωn]的导数；交点pa或pb为平底刀刀具底圆上的点，由主曲率坐标系{l1,l2,n；cc}，刀具前倾角λ、侧倾角ω、进给方向角θ，有向角度α,β表示；交点pa的微分位于其曲面投影点qa处的切空间，满足其中为曲面在pa的投影点qa处的法向量；交点pb的微分位于其曲面投影点qb处的切空间，满足其中为曲面在pb的投影点qb处的法向量，下述公式成立：

127、

128、

129、有向角度α,β的微分转化为关于前倾角λ，侧倾角ω，进给方向角θ1,θ2,…,θn的微分，得到切宽wi关于前倾角λ，侧倾角ω，进给方向角θ1,θ2,…,θn的导数；

130、使用序列二次规划求解优化问题，对于第k次迭代，优化变量的当前值为xk,ψk，求解xk,ψk附近的二次规划子问题，子问题的优化变量为增量δx,δψ

131、

132、

133、

134、ωmin≤ωik+δωi≤ωmax

135、θmin≤θik+δθi≤θmax

136、

137、其中，θik,λik,ωik为刀具在第i个切触点处第k次迭代时的进给方向角、前倾角、侧倾角；qi为每个切触点处的关节变量，qmin,qmax分别为关节的最小、最大限位，θmin,θmax分别为进给方向角的最小、最大限位，ωmin,ωmax分别为侧倾角的最小、最大限位，fλ(x)为求解刀具无干涉前倾角下限的函数；

138、二次规划子问题中的矩阵h和向量f通过下列公式计算：

139、

140、

141、其中，dsi为第i个切触点位置与第i+1个切触点位置之间的差分距离，为第i个刀位对应的第j个关节位置关于切触路径弧长参数的一阶导数，为第i个刀位对应的第j个关节位置关于切触路径弧长参数的二阶导数，k1,k2为权重值。

142、与现有技术相比，本发明具有如下的有益效果：

143、1、本发明的全局刀路优化指标同时考虑关节路径光顺性和切宽，优化变量包括刀具的进给方向角、前倾角、侧倾角，优化后的五轴平底刀端铣路径具有更加平滑的关节路径和更大的切宽，有效提升铣削加工的效率和表面质量。

144、2、本发明计算了优化目标函数关于刀具的进给方向角、前倾角、侧倾角的导数，采用了序列二次规划求解，具有较高的计算效率。

145、3、本方法可以用于复杂曲面五自由度平底刀端铣刀路优化，经优化的加工路径同时优化了刀尖点进给方向和刀轴姿态，具有更大的切宽以及更加平滑的关节路径，同时优化算法具有极高的计算效率。

146、4、本发明针对复杂曲面五自由度平底刀端铣，提出了同步优化进给方向和刀轴姿态的刀路优化方法，基于序列二次规划算法，计算了关于优化变量的解析导数，对于提升五轴平底刀端铣的加工效率与加工表面质量具有十分重要的意义和背景。