基于BAB-枚举组合法的无人机多目标攻击航迹规划求解方法

本发明属于无人机，具体涉及一种基于bab-枚举组合法的无人机多目标攻击航迹规划求解方法。

背景技术：

1、现代战争朝着智能无人化的方向发展，无人机作为无人作战的主要力量，拥有部署灵活、作战面宽、零伤亡的优势，并且体型小巧、操作灵活、适应场景多样。早期无人机主要运用于军事领域，随着智能技术的发展，无人机也逐渐用于民用领域，包括无人机巡检、无人机灌溉等。传统的无人机作战方式已经不能满足现代作战场景的需要，现阶段逐步攻关无人机群组飞行技术、集群控制技术、自主任务规划技术、人机协同作战技术，通过协同作战提高军事效能。由于无人机所具备的广泛应用价值和广阔应用场景，使其成为当前世界各国争相发展的热点。

2、航迹规划本质上是一个最优化问题，其根据任务序列及任务要求，为无人机规划出满足飞行性能和环境约束的最优航迹。无人机航迹由分布在空间中的一系列航迹点表示，其一般不包含速度和时间信息。

3、无人机航迹规划的基本方法，分为传统的优化算法和智能算法。智能算法包括遗传算法、差分进化算法等，对无人机计算能力要求较高、规划的航迹方案不满足全局最优。传统的优化算法包括优化算法、人工势场法、基于图形学的方法、数学规划方法和dubins曲线。优化算法包括粒子群算法、遗传算法和蚁群算法等，优化算法虽然能够快速规划出从起点到目标点的可行航迹，但是该类方法存在未考虑uav机动性能、规划的航迹不具有可飞性且需要对规划的航迹进行平滑处理的缺点。人工势场法简单易实现、计算时间短，规划出的路径较平滑、实时性较好；但是易陷入局部最优且障碍物附近目标不可达。基于图论的方法包括a*算法、voronoi图法、栅格法等，基于图论的方法直观、易实现、搜索效率高、收敛性强，但是当问题规模较大时，时空复杂度很高，该算法只能生成一条路径，不满足动力学约束，而且一旦任务空间发生变化，需要对空间进行重新遍历，算法的实时性较差。数学规划法包括分支定界(branch and bound，bab)法用于研究可分为多个决策阶段的组合优化问题，精确度高、鲁棒性强、规划速度快，但是解决问题的复杂度较高，适用于较小规模的航迹求解。dubins曲线由直线和一定曲率半径的弧线组成，考虑无人机起始点和终点的速度方向和大小以及无人机飞行最小转弯半径，通过几何方法计算得到两点之间的最短路径，规划出的航迹能够满足无人机的机动特性。

技术实现思路

1、为了克服现有技术的不足，本发明提供了一种基于bab-枚举组合法的无人机多目标攻击航迹规划求解方法，首先根据无人机最大武器射程和目标的威胁半径建立几何模型求解目标可打击范围；再根据目标位置坐标以及无人机最大飞行航迹建立航迹规划模型，然后通过分支定界-枚举组合方法确定各打击范围对应的全局最优打击点及打击次序，最后结合无人机的最小转弯半径采用dubins曲线依次连接各打击点得到全局最优攻击航迹。本发明方法满足无人机动力学约束的同时尽可能的节省飞行航程，提高无人机执行任务的时效性，为后续的研究以及工程应用提供新的思路。

2、本发明解决其技术问题所采用的技术方案如下：

3、步骤1：根据无人机飞行航程约束，建立航迹规划模型；

4、步骤2：根据无人机属性和目标属性建立几何模型求解目标可攻击范围；

5、步骤3：采用分支界定法和枚举法相结合的方式计算连接各可攻击区域使得攻击航迹最短的打击点；

6、步骤4：采用dubins曲线连接各目标可打击区域上的打击点，得到满足无人机动力学约束的全局最优攻击航迹。

7、进一步地，所述步骤1具体为：

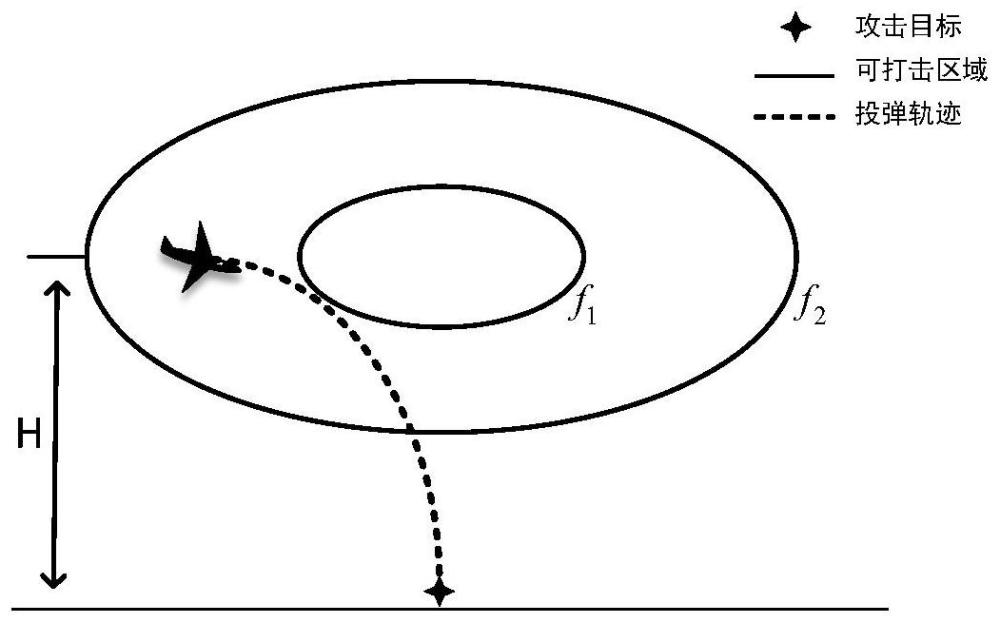
8、步骤1-1：设待打击目标点集t＝{t1,…,ti,…tn}，n为目标的总数量；ci＝{c1,…,cj}表征第i个目标点ti所对应的可打击区域边界上的所有点坐标，其中连接各可打击区域的全局路径最短的打击点用cimin表征；

9、步骤1-2：攻击航迹目标函数最小化模型：

10、

11、式中ustart为无人机起点；uend为无人机终点；d(·)表示从无人机起点出发历经所有cimin最终达到无人机终点的dubins航迹；

12、步骤1-3：设无人机在飞行的过程中无碰撞，且飞行高度保持不变，仅受到无人机最大飞行距离约束，攻击航迹最优表示为：

13、d(ustart,cimin,uend)≤duav

14、式中duav表示无人机的最大飞行航程。

15、进一步地，所述步骤2具体为：

16、步骤2-1：以目标点ti为原点建立笛卡尔坐标系；

17、步骤2-2：用f＝{f1,f2,}表征目标可攻击范围；f1表示以目标点(xi,yi)为圆心，以rmin为半径的圆，公式为：

18、

19、f2表示以目标点(xi,yi)为圆心，以rmax为半径的圆，公式为：

20、

21、f1、f2构成的圆环即为无人机可攻击范围。

22、进一步地，所述步骤3具体为：

23、步骤3-1：设i＝1；

24、步骤3-2：根据第i个目标点ti的可打击区域，计算cimin；

25、步骤3-3：设定初始分支区间，(αistart,αicenter]，(αicenter,αiend]，其中αistart＝0°、αicenter＝180°、αiend＝360°，角度α为可攻击区域边界上点与目标连线的投影与x轴形成的夹角；

26、步骤3-4：计算得到各分支区间的中间角度：

27、

28、步骤3-5：分别计算αistart和αileft所对应的位置坐标：

29、

30、式中，(x0,y0,z0)表示目标ti的位置坐标，h表示无人机的飞行高度；

31、步骤3-6：得到目标ti分支区间的参考点集pti＝[pileft,piright]t；

32、步骤3-7：如果i<n，则i加1，回到步骤3-2；否则当i＝n，进入下一步；

33、步骤3-8：得到所有可攻击区域中分支区间的参考点集pt＝{pt1,…,pti,…,ptn}；

34、步骤3-9：全排列参考点集pt，计算每一个pileft、piright全排列时全局dubins航迹长度lileft和liright，比较后进行剪支，更新分支区间，比较公式如下：

35、

36、步骤3-10：回到步骤3-2，不断缩小分支区间，直到αicenter的值不再发生改变，此时αicenter所对应坐标点即为目标ti可打击区域上使得攻击航迹最优的点cimin，其坐标为：

37、

38、本发明的有益效果如下：

39、本发明方法结合分支界定法和枚举法得到无人机多目标全局最优攻击航迹打击点及打击次序，采用dubins曲线依次连接得到全局最优攻击航迹，满足无人机动力学约束的同时尽可能的节省飞行航程，提高无人机执行任务的时效性，为后续的研究以及工程应用提供新的思路。