基于改进DP算法的壁面函数的数值模拟方法与流程

本发明涉及数值模拟领域，具体地，涉及基于改进dp算法的壁面函数的数值模拟方法。

背景技术：

1、采用壁面函数与湍流模型相结合的方式，可以显著降低壁湍流模拟对网格分辨率的依赖。然而，现有的壁面函数如von karman等人提出的经典壁面函数无法捕获黏性底层和对数律层之间的过渡区域。castro-orgaz等人构造的分段壁面函数来存在速度分布不光滑的现象。

2、为了实现湍流边界层沿壁面法向剖面的光滑连续表述，spalding提出了壁面函数统一表达公式，该公式能够在黏性底层和对数律层一致有效。其定义如下：

3、；

4、其中， y +为与壁面间的无量纲垂向距离， u +为无量纲切向速度，κ是指卡门常数，通常被近似为0.41左右， b是一个常数，取决于特定的流体条件和壁面粗糙度程度，通常取值为5.5。然而，spalding壁面函数依赖物理认知，且是一种隐式表达，在应用于湍流模拟时需要采用迭代法求解。

5、allmaras根据sa湍流模型解析推导出sa壁面函数(spalart-allmaras wallfunction)可适用于不可压湍流，其定义如下：

6、；

7、其中 y +为与壁面间的无量纲垂向距离， u +为无量纲切向速度，其他参数定义如下：、a1、b1、a2、b2、c1、c2、c3、c4均为常数。

8、she等人基于结构系综动力学理论(structural ensemble dynamics, sed)提出了多级幂函数连乘形式表达应力长度函数的分布。这项工作提供了一种独特的方式来解释和理解经验参数及其所代表的物理现象之间的复杂关系，为高保真壁面函数构造提供了思路。然而，sed理论有一些经验参数需要人工标定，这导致现有的基于壁面函数的数值模拟方法效率较低。

技术实现思路

1、本发明目的为实现无需人工标定，快速高效地得到壁面函数的模型全部参数，进而高效的实现基于壁面函数的数值模拟，并且本方法能够从粘性底层到对数律区一致有效。

2、为实现上述发明目的，本发明提供了基于改进dp算法的壁面函数的数值模拟方法，其特征在于，所述方法包括：

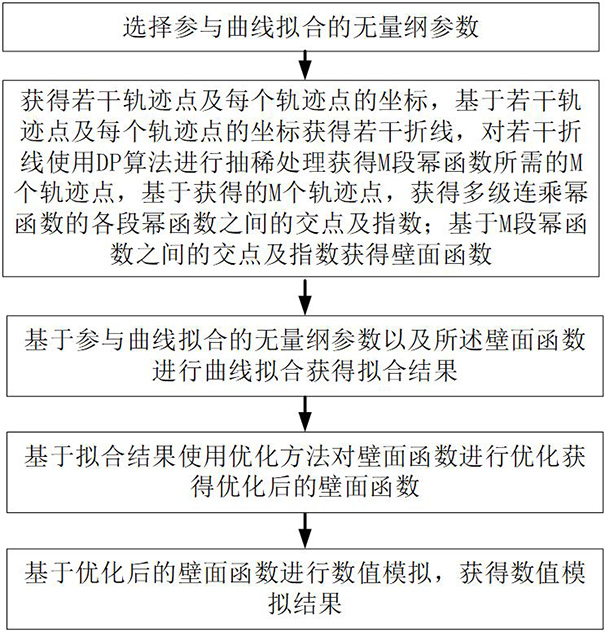
3、步骤1：选择参与曲线拟合的无量纲参数；

4、步骤2：获得若干轨迹点及每个轨迹点的坐标，基于若干轨迹点及每个轨迹点的坐标获得若干折线，对若干折线使用dp算法进行抽稀处理获得 m段幂函数所需的 m个轨迹点，基于获得的 m个轨迹点，获得多级连乘幂函数的各段幂函数之间的交点及指数；基于 m段幂函数之间的交点及指数获得壁面函数；

5、步骤3：基于参与曲线拟合的无量纲参数以及所述壁面函数进行曲线拟合获得拟合结果；

6、步骤4：基于拟合结果使用优化方法对壁面函数进行优化获得优化后的壁面函数；

7、步骤5：基于优化后的壁面函数进行数值模拟，获得数值模拟结果。

8、其中，本发明的原理是基于sed理论和dp算法的优势得来。sed理论是一种量化复杂系统的多层结构的一种理论，认为多层结构可以过一组多项式连乘的形式进行描述。使用sed的必要条件是，需要找到其中某个物理量随另一个自变量一致性较好的相似性规律。另一方面，就流动本身而言，在不可压缩壁面湍流中，传统的 y +和 u +已被证明具有较好的相似性规律，这是构造壁面函数模型的充分条件。而以往的壁面函数通常是超越函数的形式，不便于数值求解。通过简单变换，可以认为 r c等于 u +乘以 y +同样地与 y +有着良好的相似律，因此我们基于sed理论对 r c进行了标度。而dp算法由于是用简化的折线代替原本过多的折线数据点，将重要特征点提取后重建轨迹，使其近似于原始轨迹。所以能够在保持曲线基本形状的前提下，有效地简化曲线，减少存储和计算量。

9、其中，在本发明的一些实施例中，所述 m个轨迹点的获得方式为：

10、 n个轨迹点为 p1， p2，…， pn，n为轨迹点的个数，第 i个轨迹点坐标记为，将点 p1与 pn相连获得连线，将该连线作为距离参考线，将 n个轨迹点中除点 p1与 pn外的其余轨迹点向距离参考线作垂线，距离分别记为，记录下每个轨迹点到距离参考线的距离值，将所有距离值从大到小进行排序获得排序结果，基于排序结果中的前 m个距离值对应的轨迹点获得所述 m个点。

11、其中，在本发明的一些实施例中，各段幂函数的交点的获得方式为：

12、；

13、其中，为幂函数交点横坐标集合， p j( x j, y j)为第 j个轨迹点， x j为第 j个轨迹点的横坐标， y j为第 j个轨迹点的纵坐标；

14、各段幂函数指数的获得方式为：

15、；

16、其中， r j幂函数指数集合， x j-1为第 j-1个轨迹点的横坐标， y j-1为第 j-1个轨迹点的纵坐标。

17、其中，在本发明的一些实施例中，壁面函数的表达式为：

18、；

19、其中，为壁面函数输出的所有轨迹点 pi的纵坐标值， c 1为第一段幂函数系数， p为形状因子，为第 j段幂函数与第 j-1段幂函数的交点， r j-1为第 j-1段幂函数的指数， x i为轨迹点 pi的横坐标值，为第一段幂函数的固定表达形式。

20、其中，在本发明的一些实施例中，所述步骤3具体为：基于参与曲线拟合的无量纲参数以及所述壁面函数进行曲线拟合获得每一个轨迹点 pi的纵坐标值；所述步骤4具体为：由于在步骤2中得到的各段幂函数的交点及指数均为dp算法得到的初始值，若直接使用该初始值进行曲线拟合，则效果不佳，所以对得到的所有初值进行非线性优化，直到与纵坐标值相关的相对损失函数最小时则停止迭代，所述初值包括：各段幂函数交点横坐标和各段幂函数指数以及形状因子 p。

21、其中，在本发明的一些实施例中，损失函数为, y i为第 i个轨迹点的纵坐标。

22、其中，在本发明的一些实施例中，使用拟牛顿梯度法bfgs对得到的所有初值进行非线性优化。bfgs的优点在于其收敛快速，不需要二阶导数，并且具有良好的数值稳定性。其他常用的优化方法包括梯度下降法（gradient descent）适用于一些简单问题但收敛速度慢；共轭梯度法（conjugate gradient）数值稳定性不高有时无法保证收敛；随机梯度下降法（stochastic gradient descent, sgd）收敛速度可能较慢并且由于其随机性可能收敛到局部最小值并不是全局最优。

23、其中，在本发明的一些实施例中，所述方法还包括：将计算得到的值与 y i数据进行比较获得比较结果，基于比较结果获得壁面函数拟合的准确性评估结果。

24、本发明提供的一个或多个技术方案，至少具有如下技术效果或优点：

25、本方法能够从粘性底层到对数律区一致满足，保持了壁面函数的统一性，不会造成流场基本量的不连续性。

26、本方法利用dp算法所得初值可自动迭代出最优参数集合。

27、本方法给出了损失函数，可得到损失函数最小时的参数集合。

28、将采用本发明方法构造的基于 r c的壁面函数植入cfd流体动力学仿真求解程序，无需迭代求解，适用性较强，效率较高。