电动汽车有序充放电调度方法、存储介质及设备

本发明涉及电动汽车能源管理，特别是涉及一种电动汽车有序充放电调度方法。

背景技术：

1、电动汽车的有序充放电调度优化对电力系统的稳定运行至关重要。随着电动汽车数量的迅速增长，其对电网的影响日益显著。电动汽车充放电需求的随机性和波动性对电网的负荷平衡和运行稳定性提出了挑战。因此，如何有效地对电动汽车的充放电进行调度和优化，以确保电力系统的平稳运行，已成为当前研究的热点问题。

2、目前，针对电动汽车有序充放电调度的方法主要包括需求响应调度和智能充电管理。需求响应调度基于用户的充电需求，通过调整充电桩的使用来实现电动汽车的有序充放电，这种调度方式依赖于用户的高度配合，非常影响用户体验。而智能充电管理可以实现远程监控和集中管理充电桩，但其依赖于准确的数据支持和高效的算法，目前的智能充电管理，例如中国专利公开号为cn117048408a的发明专利所公开的一种电动汽车双向充电智能管理系统，通过随时采集每一智能充电桩的工作状态，根据工作状态来确定每一正在工作的目标智能充电桩，将目标智能充电桩和对应的充电电车进行双向通信，从而采集充电电车的充电数据和目标智能充电桩的工作数据，通过解析两组数据得到对应的充电信息和工作信息，然后根据充电信息确定充电电车所适用的充电模式，在必要情况下将目标智能充电桩的供电模式进行调节，从而适应于充电电车的需要，然而该种方法不能够综合考虑供电侧及用户侧的需求，无法实现区域内净负荷峰谷差最小化和车主综合用电成本最小化，同时系统的安全性及可靠性不佳。

技术实现思路

1、发明目的：本发明的目的是提供一种高效、可靠、鲁棒性高、智能化程度高的电动汽车有序充放电调度方法。

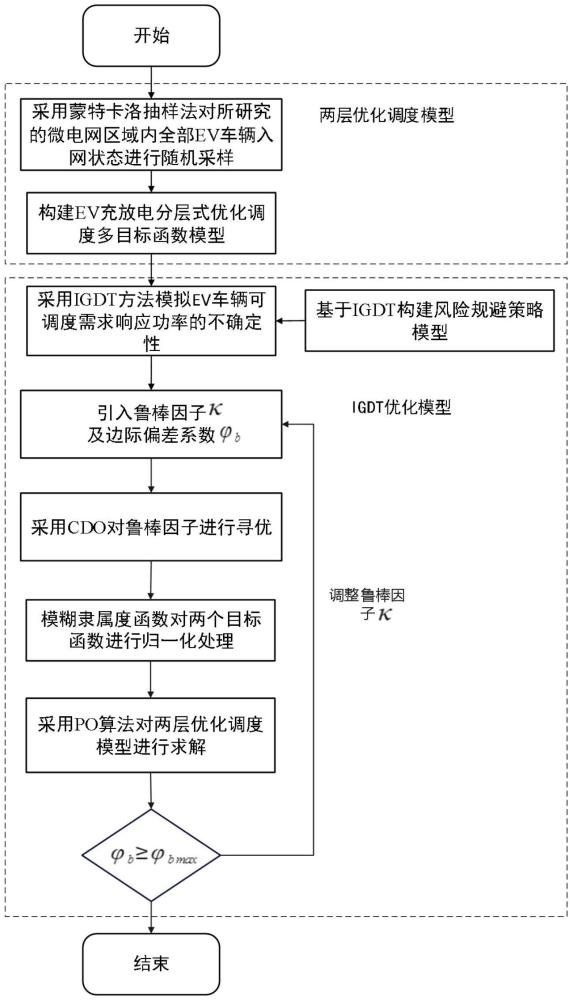
2、技术方案：本发明的一种电动汽车有序充放电调度方法，基于区域净负荷峰谷差和用户综合用电成本建立两层优化调度模型，通过po算法对两层优化调度模型进行求解，具体包括以下步骤：

3、s1：采用蒙特卡洛抽样方法确定该区域ev用户有序调度策略响应度，基于系统稳定性和经济性构建配电层和用户层两层优化调度模型并建立相应的目标函数；

4、s2：采用igdt方法模拟ev车辆可调度需求响应功率的不确定性，引入偏差系数并构建风险规避策略模型；

5、s3：采用cdo算法对风险规避策略模型中的鲁棒因子进行优化；

6、s4：对两层优化调度模型中两个目标函数进行模糊归一化处理，并将的求解变换为对偏差系数的求解，采用po算法对两层优化调度模型进行求解。

7、进一步的，所述s1中采用蒙特卡洛抽样方法对所研究的微电网区域内全部ev车辆入网状态进行随机采样，以确定该区域ev用户有序调度策略响应度，其中，有序调度策略中ev进行充、放电所需的功率为：

8、

9、式中，r(t)为ev用户t时刻有序调度策略响应度；rc(t)、rf(t)分别为ev用户t时刻有序调度策略充、放电响应度；s为微电网区域内总的ev车辆数；nc(t)、nf(t)分别为ev用户响应有序调度策略时充、放电的ev数量；pd(t)、pl(t)分别为在t时刻下采用无序、有序策略下的总负荷功率；pl,c(t)、pl,f(t)分别为有序策略下ev车辆充、放电所需的功率；pic(t)、pif(t)分别为第i辆车的充电和放电额定功率；hs(t)＝1表示此时ev车辆处于充电状态；hs(t)＝0表示此时ev车辆处于静止状态。

10、进一步的，所述s1中在主网调度中心建立配电层模型进行电网侧优化，配电层模型以区域净负荷峰谷差波动最小为第一个目标函数：

11、f1＝min(pj,max(t)-pj,min(t))

12、pj(t)＝pl(t)+pev(t)

13、式中，pj(t)为t时刻区域净负荷；pl(t)，pev(t)分别为t时刻的基础负荷和ev总充放电功率；

14、用户层模型以车主综合用电成本最低为第二个目标函数：

15、

16、式中，nc,t和nf,t分别为t时刻内充、放电ev数量；pc,n(t)和pf,n(t)分别为t时刻ev的充、放电功率；pc,t和pf,t分别为t时刻ev的充、放电电价；ξc和ξf分别为ev充、放电效率；cb为ev放电产生的电池损耗；δt为单位控制时间段长度。

17、进一步的，所述配电层模型在优化过程中满足的如下约束条件：

18、(1)功率平衡约束

19、ps(t)＝pl(t)+pev(t)

20、式中，ps(t)为t时刻变电站给充电桩供电值；pev(t)为t时刻ev总充放电功率；pl(t)为t时刻的基础负荷；

21、(2)ev充放电功率约束

22、ps(t)min≤pev(t)≤ps(t)max

23、式中，ps(t)min和ps(t)max分别为变电站给充电桩最小和最大供电值；pev(t)为t时刻ev总充放电功率；

24、(3)单辆ev荷电状态值约束

25、socmin≤soc(t)≤socmax

26、式中，soc(t)为t时刻ev总的荷电状态；socmin，socmax分别为荷电状态的最小值和最大值。

27、进一步的，所述用户层模型在优化过程中满足如下约束条件：

28、(1)单辆ev充放电功率约束

29、

30、式中，pc,n(t)和pf,n(t)分别为t时刻ev的充、放电功率；ξc和ξf分别为ev充、放电工作效率；和分别为ev正常工作的最大充放电功率；

31、(2)单辆ev可充放电时段约束

32、tin,n≤tn≤tout,n

33、式中，tn为进行有序调控策略的时间段；tin,n，tout,n分别为第n辆ev接入和离开电网的时间。

34、(3)单辆ev车主电量期望约束

35、αn≤socn(tout,n)

36、式中，αn为车主n设定的ev荷电状态期望值；socn(tout,n)为第n辆ev离网时的荷电状态。

37、进一步的，所述s2中采用igdt方法模拟ev车辆可调度需求响应功率的不确定性，协调电动汽车充放电功率，降低区域净负荷峰谷差波动和车主的综合用电成本，经igdt优化后的不确定性模型：

38、

39、式中，f(x,ν)为目标函数；x为决策变量；mmax为引入不确定量的偏差系数χ后ev车辆可调度需求响应功率的最大值；υ为输入参数；h(x,ν)、g(x,ν)分别为等式、不等式约束。

40、决策变量x的表达式：

41、

42、式中，为t时段ev车辆可调度需求响应功率的预测值；x为t时段ev车辆可调度需求响应功率的实际值；χ为不确定量的偏差系数。

43、令决策变量为x0、x1，建立ev车辆不确定量的优化模型：

44、

45、式中，o(x1,x)＝0、p(x0,x1)≤0分别为等式、不等式约束；x0、x1为两个不同的决策变量；

46、采用风险规避策略，在满足目标函数约束条件的情况下，寻求系统能承受的最大不确定性，以提升模型的鲁棒性及系统规避风险的能力，基于igdt构建的风险规避策略模型如下：

47、

48、式中，f1*为电网能接受的不确定性带来的调度成本增加的最大值；fb为调度成本的基准值；(1+κ)fb为风险规避调度成本的预期值；κ为鲁棒水平因子；ps(t)为t时刻变电站给充电桩供电值；为t时段ev车辆可调度需求响应功率的预测值；x为t时段ev车辆可调度需求响应功率的实际值；δχ和δf1分别为偏差系数和运行费用波动量；为边际偏差系数。

49、进一步的，所述s3中通过计算α、β、γ粒子的梯度下降过程转化为数学模型，从而实现对风险规避策略模型中重要参数的优化：

50、计算α粒子攻击人类时的梯度下降因子vα：

51、vα＝0.25·(xα(t)-ρα·δα)

52、

53、xh＝r2·π

54、sα＝log(rand(1:16,000))

55、δα＝|aα·xα(t)-xt(t)|

56、aα＝r2·π

57、式中，xα(t)为α粒子的当前位置；ρα为α粒子的传播；δα为人体位置与α粒子位置之间的差值，xh为人活动的圆形区域面积，sα为α粒子的速度，δα为α粒子位置和总位置之间的差，aα为α粒子传播的圆形面积，xt为总位置的平均值；

58、计算β粒子攻击人类时的梯度下降因子vβ：

59、vβ＝0.5·(xβ(t)-ρβ·δβ)

60、

61、xh＝r2·π

62、sβ＝log(rand(1:270,000))

63、δβ＝|aβ·xβ(t)-xt(t)

64、aβ＝r2·π

65、式中，xβ(t)为β粒子的当前位置，ρβ为β粒子的传播，δβ为人体位置与β粒子位置之间的差值，xh为人活动的圆形区域面积，sβ为β粒子的速度，δβ为β粒子位置和总位置之间的差，aβ为β粒子传播的圆形面积，xt为总位置的平均值；

66、计算γ粒子在攻击人类时的梯度下降因子vγ：

67、νγ＝(xγ(t)-ργ·δγ)

68、

69、xh＝r2·π

70、sγ＝log(rand(1:300,000))

71、δγ＝|aγ·xγ(t)-xt(t)|

72、aγ＝r2·π

73、式中，xγ(t)为γ粒子的当前位置，ργ为γ粒子的传播，δγ为人体位置和γ粒子位置之间的差值，xh为人活动的圆形区域面积，sγ为γ粒子的速度，δγ为γ粒子位置和总位置之间的差，aγ为γ粒子传播的圆形面积，xt为总位置的平均值；

74、根据运动方程求出这些粒子的总速度的平均值：

75、

76、cdo算法通过α、β、γ三个辐射粒子的攻击方式，获取风险规避策略模型中鲁棒因子κ的最优值，进而优化风险规避策略模型的效果。

77、进一步的，所述s4包括以下步骤：

78、s41：采用模糊隶属度函数对两个目标函数进行归一化处理：

79、

80、式中，f1，min、f2，min和f1,min+ρ1f1,min、f2,min+ρ2f2,min分别为综合运行费用、负荷需求波动量的最优值与微电网所能接受的最高、最低值；不同情况下的弹性满意度系数为ρ1、ρ2；y1(f1)、y2(f2)分别为综合运行费用和负荷波动量满意度的目标函数；

81、s42：将目标函数中的f1的求解变换为对偏差系数χ的求解：

82、

83、式中，ρ3为弹性满意度；χ为偏差系数；χmax为最大偏差系数；y3(f3)为优化后的综合运行费用满意度的目标函数；

84、s43：将两个满意度y2(f2)、y3(f3)分别赋予权重系数λ1、λ2并加权处理的综合满意度f表示为：

85、

86、式中，λ1、λ2和y2(f2)、y3(f3)分别为权重系数和所优化的两个满意度的目标函数；

87、s44：采用po鹦鹉优化器对两层优化模型进行求解，po算法通过模拟训练有素的鹦鹉的关键行为来解决优化问题，包括以下步骤：

88、初始化两层优化模型的解，公式如下：

89、xi0＝lb+rand(0,1)*(ub-lb)

90、式中，rand(0,1)表示[0，1]范围内的随机数；lb、ub分别为综合满意度目标函数解的上下限。

91、觅食行为过程可表示为：

92、

93、式中，表示当前的解；表示后续更新的解；表示解的均值；xbest表示目前的最优解；t为迭代次数；maxiter为最大迭代次数；levy(dim)为levy分布的函数形式，其中dim代表维度；

94、levy分布的函数形式计算公式为：

95、

96、式中，μ为levy分布的期望值；σ为levy分布的标准差；ν为levy分布的标准差；μ～n(0,dim)、ν～n(0,dim)表示μ、ν服从正态分布；γ为levy分布的指数；γ为伽玛函数；

97、停留行为过程可表示为：

98、

99、式中，ones(1,dim)表示维度为dim的全1向量；

100、交流行为过程可表示为：

101、

102、式中，p为[0，1]范围内随机生成的概率值；

103、怕生行为过程可表示为：

104、

105、po算法通过不断模拟鹦鹉的觅食行为、停留行为、交流行为、怕生行为，最终获取两层优化模型的最优解。

106、本发明的一种存储介质，用于计算机可读存储，所述存储介质存储有一个或者多个程序，所述一个或者多个程序可被一个或者多个处理器执行，以实现上述的电动汽车有序充放电调度方法的步骤。

107、本发明的一种存储设备，包括控制器、存储器、存储在所述存储器上并可被所述控制器执行的计算机程序以及用于实现所述控制器和所述存储器之间的连接通信的数据总线，其中所述计算机程序被所述控制器执行时，实现如上所述的电动汽车有序充放电调度方法的步骤。

108、有益效果：与现有技术相比，本发明具有以下显著优点：(1)减小峰谷差波动：本发明通过蒙特卡洛方法对微电网区域内全部ev车辆入网状态进行随机采样，确定ev用户有序调度策略的响应度，帮助减小微电网区域内的净负荷峰谷差波动，提高电网的稳定性；(2)控制综合用电成本：本发明采用ev充放电分层式优化调度策略，建立两层优化调度模型，有效控制ev用户的综合用电成本，使其在充放电过程中更加经济高效；(3)有效管理不确定性：本发明考虑到ev用户响应有序调度策略的不确定性，采用igdt方法模拟ev车辆可调度需求响应功率的不确定性。通过风险规避策略，确保在满足目标函数约束条件的情况下，系统能够承受最大的不确定性；(4)快速优化计算：本发明通过使用切诺贝利灾难优化器(cdo)，加速模型优化计算的速度，实现在较短的时间内找到更优的解决方案；(5)高效协调不同目标：本发明针对区域净负荷峰谷差和用户综合用电成本两个矛盾目标函数，采用模糊隶属度函数对这两个目标函数进行归一化处理，有效协调不同目标之间的权衡，使系统能够更好地平衡运行费用和负荷波动量；(6)全面提升全局搜索能力：本发明通过鹦鹉优化器(po)对两层优化模型进行求解，可以获得全局搜索能力，从而找到更优的解决方案。