邻近地下既有结构的基坑侧壁开挖面极限支护力计算方法

本发明属于深基坑支护，具体涉及一种邻近地下既有结构的基坑侧壁开挖面极限支护力计算方法。

背景技术：

1、本部分的陈述仅仅是提供了与本发明相关的背景技术信息，不必然构成在先技术。

2、在地下轨道交通大规模建设和tod模式日益发展的背景下，地铁车站与周边地下结构的建设将会相互耦合，形成多功能地下综合体。在结构综合体靠近地铁车站的建设过程中，通常需要在开挖深基坑时对连通位置的围护结构进行破除，这一过程类似于盾构始发。在隧道开挖面稳定性分析中，极限平衡法被广泛应用。

3、针对开挖面极限支护力的理论计算公式推导，horn通过分析大量开挖面失稳区域，总结出开挖面失稳区域几何轮廓的基本特征，提出了经典的三角形楔体-筒仓模型，如图1，用于分析土体开挖面的失稳情况及评估土体的极限支护压力。这个模型将复杂的几何形态简化为相对简单的几何结构，推导过程逻辑清晰且适应性强，已在诸多研究中得到广泛应用和改进。

4、由于既有结构的存在，结构间土体的受力状态及边界条件与常规开挖面不同，因此需要明确前方既有结构对开挖面失稳破坏形态的影响机理；三角形楔体-筒仓模型无法适用于开挖面前方存在既有结构的情况，无法准确求出开挖面前方存在既有结构时，基坑侧壁矩形开挖面极限支护力。

技术实现思路

1、针对上述问题，本发明提供一种邻近地下既有结构的基坑侧壁开挖面极限支护力计算方法，能够求得开挖面前方存在既有结构时，基坑侧壁矩形开挖面极限支护力。

2、为实现上述目的，本发明采取以下技术方案：

3、一种邻近地下既有结构的基坑侧壁开挖面极限支护力计算方法，包括以下步骤：

4、s1、收集基坑设计参数及地质参数，确定开挖深度、开洞范围宽高、地下既有结构与洞口开挖面的水平距离 l（以下简称近接距离 l）、地下既有结构的埋置深度和高度、土重度、内摩擦角、粘聚力、泊松比等参数；

5、s2、对楔形体滑动破裂面与水平面夹角 α与近接距离 l进行指数拟合，得出其关系表达式，通过近接距离 l确定楔形体滑动破裂面与水平面夹角 α；

6、s3、考虑地下既有结构对竖向剪切滑移面的显著限制作用，所以在靠近既有结构一侧，土体的剪切滑移带呈直线，沿既有结构表面向上延伸至上部松动区；由于侧向土压力作用，当剪切滑移面滑动时，将在竖向滑移面产生竖直向上的摩擦力和黏聚力；

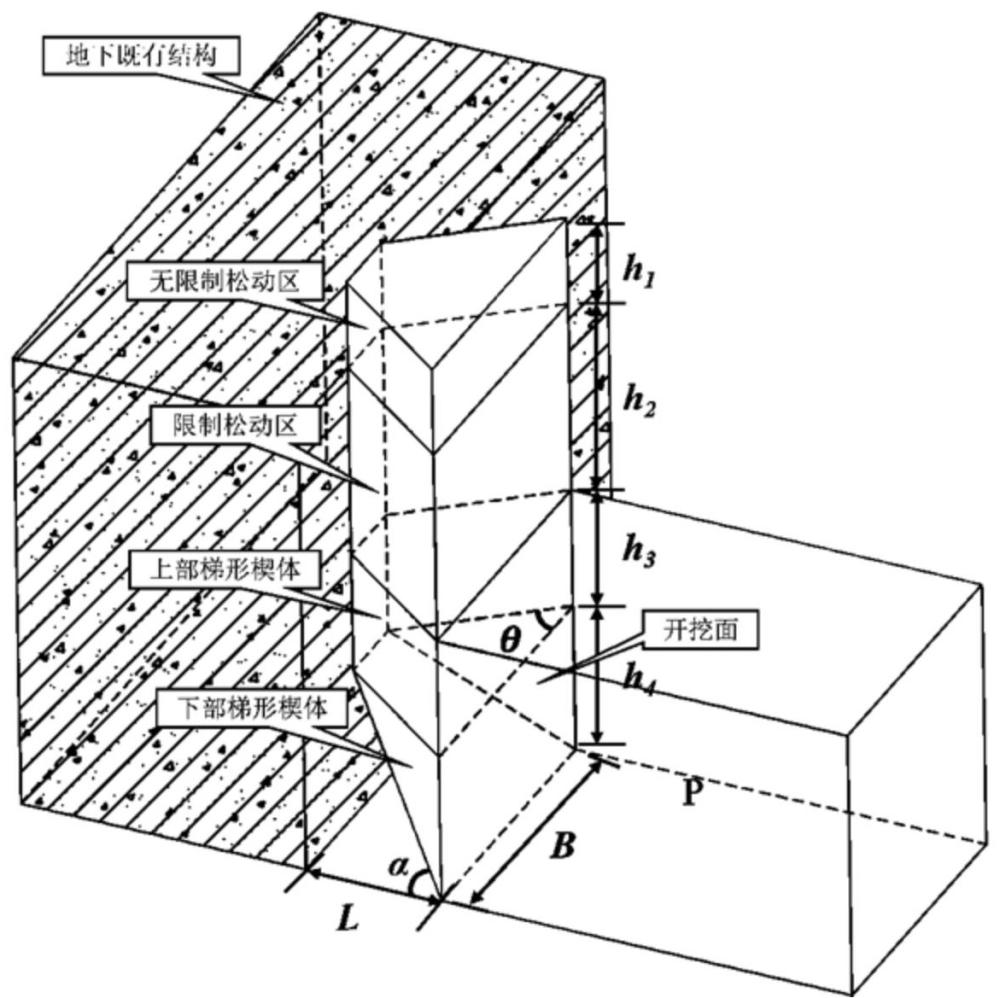
7、s4、结合楔形体滑动破裂面与水平面夹角 α与近接距离 l的关系表达式及垂直滑动面上的摩擦力和黏聚力，对经典的三角形楔体-筒仓模型进行修正，建立适用于开挖面前方存在既有结构的梯形楔体-筒仓模型；

8、s5、先对梯形楔体-筒仓模型进行受力分析，并根据力的平衡建立开挖面极限支护力 p的平衡方程；

9、s6、再建立梯形楔体-筒仓模型的坐标系统，对s5中所述的开挖面极限支护力p平衡方程中的各个分量值进行求解，并将求解结果代入开挖面极限支护力p的平衡方程计算求得 p值。

10、优选的，所述步骤s2中， α角与 l关系表达式为：；

11、式中：

12、 α表示楔形体滑动破裂面与水平面夹角；

13、 l表示地下既有结构与洞口开挖面的水平距离，m。

14、优选的，所述步骤s4中，模型建立的假设限定条件需要满足：

15、1）土体为单一匀质理想弹塑性土体，并遵循mohr-coulomb强度准则；

16、2）开挖面楔形体模型分上下两部分，开挖面顶部以下为梯形楔体，根据夹角 α将其分为上下两层锲形体，上层楔形体高度为，下层楔形体高度为；

17、开挖面顶部以上为梯形棱柱体结构，分为限制松动区，高度为 h2，和无限制松动区，高度为 h1；

18、滑裂面的底边宽度为洞口宽度，且楔形体滑动破裂面与水平面夹角 α与近接距离 l存在函数关系；

19、3）楔体顶面及倾斜滑动面应力为均匀分布，侧面竖向应力沿深度方向线性分布。

20、优选的，所述步骤s5中，开挖面极限支护力p的平衡方程为：

21、；

22、其中：

23、；

24、式中：

25、 p表示开挖面极限支护力；

26、 t1表示梯形楔体前方垂直滑动面上的摩擦力；

27、 c1表示梯形楔体前方垂直滑动面上的黏聚力；

28、 c2表示梯形楔体倾斜滑动面上的黏聚力；

29、 t3表示梯形楔体侧方垂直滑动面上的摩擦力；

30、 c3表示梯形楔体侧方垂直滑动面上的黏聚力；

31、 n3表示梯形楔体侧方垂直滑动面上的法向力；

32、 n4表示筒仓底部竖向合力；

33、表示土体内摩擦角；

34、 g表示梯形楔体自重；

35、 θ表示梯形楔体夹角，假定为50°；

36、开挖面受到的极限支护应力为：。

37、优选的，所述步骤s5中，摩擦力和黏聚力计算公式为：

38、；

39、式中：

40、表示梯形楔体侧向土压力系数；

41、表示梯形楔体-筒仓与既有结构（或支护结构）摩擦系数，取0.6；

42、表示土体重度；

43、b表示矩形开挖面宽度，m；

44、表示筒仓底部竖向土压力，；

45、 dz3表示上部楔体中微元体厚度， z3表示上部楔体中微元体到上部楔体上表面的距离。

46、优选的，所述筒仓底部竖向合力关系式为：

47、；

48、式中：

49、表示无限制松动区土体的侧面摩擦力；

50、表示限制松动区土体的侧面摩擦力；

51、 a表示梯形截面面积；

52、表示限制松动区与无限制松动区自重应力之和；

53、其中，；

54、；

55、；

56、式中：

57、—无限制松动区顶面竖向土压力，=（地表荷载）；

58、 dz1表示无限制松动区中微元体厚度， z1表示无限制松动区中微元体到无限制松动区上表面的距离；

59、；

60、式中：

61、—限制松动区顶面竖向土压力，=；

62、 dz2表示制松动区中微元体厚度， z2表示制松动区中微元体到限制松动区上表面的距离。

63、优选的，所述滑动面的摩擦力和黏聚力关系式为：

64、；

65、式中：

66、表示土体粘聚力；

67、表示筒仓底部竖向土压力，。

68、优选的，所述梯形楔体侧方垂直滑动面上的法向力 n3关系式为：

69、。

70、优选的，所述梯形楔体倾斜滑动面上的黏聚力关系式为：

71、。

72、优选的，所述梯形楔体自重 g关系式为：

73、。

74、与现有技术相比，本发明具有的优点和积极效果是：

75、本发明基于数值模拟和室内试验，分析开挖面前方存在既有结构时的失稳破坏形态，结合楔形体滑动破裂面与水平面夹角 α与近接距离 l的关系表达式及垂直滑动面上的摩擦力和黏聚力，对经典的三角形楔体-筒仓模型进行修正，建立了适用于开挖面前方存在既有结构的梯形楔体-筒仓模型。对模型中的梯形楔体进行受力分析，根据受力平衡，建立开挖面极限支护力 p的平衡方程；建立梯形楔体-筒仓模型坐标系统，求解开挖面极限支护力p平衡方程中的各个未知分量值，将求解的结果最终代入开挖面极限支护力 p的平衡方程计算求得开挖面前方存在既有结构时，基坑侧壁矩形开挖面极限支护力。