一种弱模型依赖的高超声速变形飞行器智能控制方法

本发明属于航空航天飞行器控制领域，涉及一种弱模型依赖的高超声速变形飞行器智能控制方法。

背景技术：

1、高超声速变形飞行器的特点包括快速飞行、远距离和强大的突防能力。通过优化气动配置，这种飞行器不仅改善了气动特性，还扩大了飞行包络，提高了能源效率，并增强了对环境的适应性及任务调整的灵活性。尽管可变性能力增强了气动特性，但也为控制系统的设计增加了挑战，特别是在变形过程中，飞行器的强耦合、非线性和多模态特征使得精确控制更加困难。因此，开发鲁棒控制器，减少数据传输和执行机构频率，确保系统姿态稳定是至关重要的。

2、考虑到高超声速变形飞行器的高度非线性、强时变特性、强耦合特性和不确定性大的问题，同时又对复杂飞行环境和飞行任务调整具有较强的调整能力，传统的控制方法难以满足较高的稳定性、鲁棒性和控制精度要求。而变形阶段飞行控制又会造成飞行器系统数据传输压力，以及执行机构频繁动作等问题，进一步强化了控制系统的设计难度。基于先进控制理论的控制方法均依赖于对被控对象的高精度建模，难以应对现代高速飞行器的姿态控制需要。因此，若要从根本上解决现有姿态控制方法与现实需求之间的矛盾，必须降低控制方法对模型的依赖程度，以提高对模型不确定性的适应性，增强对不同气动外形的通用性，有必要建立一套针对高超声速变形飞行器的弱模型依赖智能控制方法。

3、宋申民、孙经广、王岩等在“一种基于非线性函数的高超声速飞行器跟踪控制方法”（cn108427289b）中引入了一个新的连续可微的非线性饱和函数，并结合自适应理论，设计了非线性鲁棒控制器，解决现有飞行器的控制模型复杂及鲁棒性差的问题。然而，该专利是基于自适应控制理论的实时控制，其研究对象并未考虑高超声速飞行器的变形影响，并且所涉及的方法需要涵盖连续可微的非线性饱和函数，并没有考虑模型信息较少情况下的飞行控制问题，以及对控制品质的关注较为弱化。

4、胡庆雷、李梓明、郭雷等在“基于神经网络的高超声速飞行器自适应补偿控制方法”（cn108375907a）中构建平滑函数来估计非线性输入饱和，并引入径向基函数神经网络来估计高超声速飞行器的纵向动力学模型中的非线性函数，通过反步法设计高超声速飞行器的自适应补偿控制器及相应的自适应参数更新律，解决了高超声速飞行器飞行过程中各类升降舵故障以及执行器饱和对飞行器的影响，保证了系统的容错能力和鲁棒性。该专利利用径向基函数神经网络来估计高超声速飞行器的纵向动力学模型中的非线性函数，该方法并没有阐述如何对高超声速飞行器的形变影响进行修正补偿，更新律的设计导致在线数据计算频繁，不适合高动态下的强适应控制，并且该方法一定程度上需要保证模型具有仿射形式，对控制效果的考虑较少，存在一定的局限性。

5、陈浩岚、王鹏、汤国建在“变形飞行器输出误差受限与输入饱和控制方法”（见《航空学报》，2023年8月，第15期，页码400-411）中，基于双曲正切函数与辅助系统得到了面向输入饱和的控制系统，并设计了转换误差使系统能在更为宽松的收敛条件下实现输出误差受限控制。该论文利用转换误差使系统实现输出误差受限控制，但该方法并不适用于具有非仿射特征的高超声速变形飞行器控制需求，动态非线性不仅依赖于系统的状态，而且依赖于控制输入，无法适应变形控制任务的使用。

6、何晟在“弹性高超声速变形飞行器强鲁棒控制方法研究”（见《国防科技大学》，2021年硕士毕业论文，页码38-50）中，提出了基于神经网络的弹性高超声速变形飞行器自适应控制方法。利用神经网络对未知模型进行非线性逼近，结合动态面反步控制思想，完成整体控制器设计，能够实现变形过程稳定控制。然而，该方法不适用于具有非仿射特征的高超声速变形飞行器控制需求，且引入反步控制会导致算法计算量增加，而且较多的控制参数使得控制器的实际使用更加复杂。

7、王子健、张书宇、侯明哲在“基于在线参数辨识的变体飞行器控制”（见《兵器装备工程学报》，2022年10月，第10期，页码60-65）中，设计了一种在线时变参数辨识算法，确定外形变化导致气动系数的不确定性与外界扰动等因素对飞行器产生的影响，通过固定时间收敛的状态反馈控制策略保证飞行器的机动性能。然而，该方法依赖于系统建模的精确性，这可能导致姿态控制方法与实际飞行任务需求之间的矛盾，使得控制精度受限于辨识精度和建模精度。在处理具有强时变特性、强耦合特性和高度不确定性的控制问题时，应用此方法存在一定的难度。

技术实现思路

1、本发明提出的针对高超声速变形飞行器设计弱模型依赖智能控制方法，充分考虑到高超声速变形飞行器的高度非线性、强时变特性、强耦合特性和不确定性大的问题，通过设计弱模型依赖智能控制方法降低控制方法对模型的依赖程度，以提高对模型不确定性的适应性，增强对不同气动外形的通用性，根本上解决现有姿态控制方法与现实需求之间的矛盾。通过设计基于数据堆栈的两步更新策略，应对变形阶段飞行控制造成飞行器系统数据传输压力，以及执行机构频繁动作等问题，进一步强化了控制系统在线应用的可操作性。

2、本发明的技术方案具体如下：

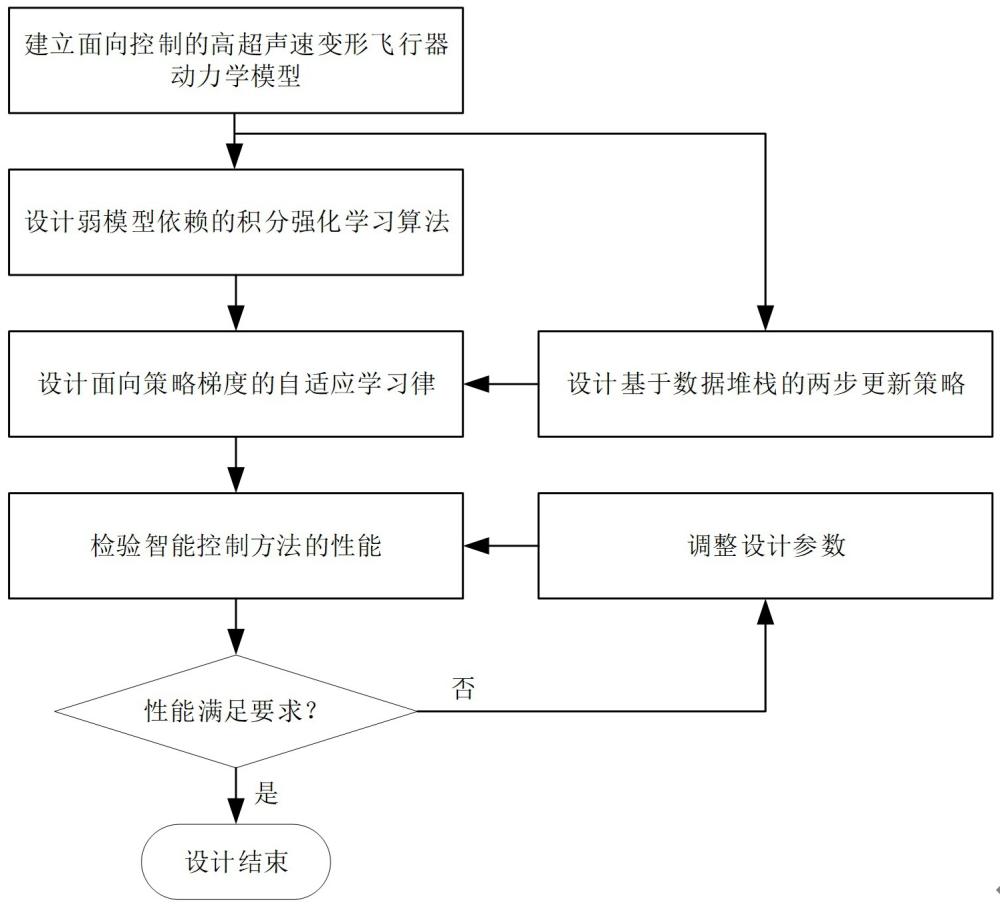
3、一种弱模型依赖的高超声速变形飞行器智能控制方法，包括如下步骤：

4、（1） 建立面向控制的高超声速变形飞行器动力学模型

5、为适应不同工况的任务需求，将变后掠飞行器的纵向模型表述为如下形式：

6、(1)

7、式中：v是速度，是速度的导数，h是高度，是高度的导数，α是攻角，是攻角的导数，θ是俯仰角，是俯仰角的导数，q是俯仰角速率，是俯仰角速率的导数，iyy是俯仰转动惯量，m是飞行器质量；t为发动机推力，d为飞行阻力，l为飞行器升力，m是俯仰力矩，且表示为：

8、(2)

9、式中：为推力系数，为燃油当量比，为升降舵指令。ρ为空气密度，为机翼参考面积，为平均几何弦长，表示升力系数，表示阻力系数，表示俯仰力矩系数。

10、为翼展变形率，取值范围为<mstyle displaystyle="true" mathcolor="#000000"><mstyle displaystyle="true" mathcolor="#000000"><mi>ξ</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><msub><mrow /><mstyle displaystyle="true" mathcolor="#000000"><mi>b</mi></mstyle></msub></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>∈</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mo>[</mo><mrow><mn>0</mn><mi>,</mi><mn>1</mn></mrow><mo>]</mo></mstyle></mstyle>，为后掠角变形率，取值范围为<mstyle displaystyle="true" mathcolor="#000000"><mstyle displaystyle="true" mathcolor="#000000"><mi>ξ</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><msub><mrow /><mi>s</mi></msub></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>∈</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mo>[</mo><mrow><mn>0</mn><mi>,</mi><mn>1</mn></mrow><mo>]</mo></mstyle></mstyle>，分别定义如下：

11、(3)

12、式中：b为翼展；bmin和bmax分别为飞行器无变形时的翼展以及最大形变时的翼展；s为后掠角；smin和smax分别为飞行器无形变时的后掠角以及最大形变时的后掠角。升力系数cl，阻力系数cd，俯仰力矩系数cm函数关系定义如下：

13、(4)

14、式中：为攻角为0时升力与形变量的系数关系，为升力与攻角的系数关系，为升力与降舵指令的系数关系；为攻角为0时升力与形变量的系数关系，为升力与攻角的系数关系，为升力与攻角平方项的系数关系；为攻角为0时俯仰力矩与形变量的系数关系，为俯仰力矩与攻角的系数关系，为升力与降舵指令的系数关系。

15、（2） 设计弱模型依赖的积分强化学习算法

16、将翼展变形率和后掠角变形率视为额外的控制输入，得到如下的系统模型：

17、(5)

18、式中：<mstyle displaystyle="true" mathcolor="#000000"><mi>x</mi><mrow><mo>(</mo><mi>t</mi><mo>)</mo></mrow><mi>=</mi><msup><mrow><mo>[</mo><mrow><mi>v</mi><mi>,</mi><mi>α</mi><mi>,</mi><mi>θ</mi><mi>,</mi><mi>q</mi><mi>,</mi><mi>h</mi></mrow><mo>]</mo></mrow><mi>t</mi></msup></mstyle>为状态向量，是状态向量的导数；<mstyle displaystyle="true" mathcolor="#000000"><mi>u</mi><mrow><mo>(</mo><mi>t</mi><mo>)</mo></mrow><mi>=</mi><msup><mrow><mo>[</mo><mrow><mstyle displaystyle="true" mathcolor="#000000"><mi>δ</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><msub><mrow /><mi>e</mi></msub></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>,</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>δ</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><msub><mrow /><mi>t</mi></msub></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>,</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>ξ</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><msub><mrow /><mstyle displaystyle="true" mathcolor="#000000"><mi>b</mi></mstyle></msub></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>,</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>ξ</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><msub><mrow /><mstyle displaystyle="true" mathcolor="#000000"><mi>s</mi></mstyle></msub></mstyle></mrow><mo>]</mo></mrow><mi>t</mi></msup></mstyle>为控制输入向量；描述了状态向量的一阶导数与状态、输入构成的函数关系，<mstyle displaystyle="true" mathcolor="#000000"><mstyle displaystyle="true" mathcolor="#000000"><mi>y</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>(</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>t</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>)</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>=</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>h</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>(</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>x</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>)</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>=</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mo>[</mo><mrow><mi>v</mi><mi>,</mi><mi>α</mi><mi>,</mi><mi>θ</mi><mi>,</mi><mi>q</mi><mi>,</mi><mi>h</mi></mrow><mo>]</mo></mstyle><mstyle displaystyle="true" mathcolor="#000000"><msup><mrow /><mi>t</mi></msup></mstyle></mstyle>为输出向量。

19、公式(5)的系统模型为非仿射系统，因此设计基于演员评论家网络的高超声速变形飞行器积分强化学习策略，具体如下：

20、首先给出q函数的表达式：

21、(6)

22、其中，表示与状态量x(t)和控制输入量u(t)相关的函数，是评论家网络的权值向量，表示lc维的向量组，分别表示是权值向量的lc个子向量，是评论家网络的基向量，分别表示是评论家基函数的lc个子向量。

23、相似地，对于策略函数存在一个权值向量组，使得

24、(7)

25、其中，表示在策略函数下产生的控制量，是演员网络的权值矩阵，表示la行4列的矩阵，分别表示演员网络权值向量的la个子向量；是演员网络的基向量，表示la行1列的向量，分别表示是演员网络基向量的la个子向量。定义评论家网络逼近误差为，定义演员网络逼近误差为，这两个误差随着向量矩阵包含的信息量的增加而趋近于0。

26、然后，定义最优动作-价值函数和最优动作值。由于理想的权重是未知的，相应的和也难以计算得到。因此，采用评论家网络和演员网络进行逼近，表示为如下形式：

27、(8)

28、其中，表示与状态量x和控制量u相关的动作-价值函数估计值，表示与状态量x相关的动作估计值，和分别是评论家网络权重wc和演员网络权重wa的估计值。基于演员-评论家结构，对公式（8）中的策略迭代积分强化学习的控制量u进行优化整定。

29、（3） 设计面向策略梯度的自适应学习律

30、基于策略梯度的积分强化学习算法可以通过演员和评论家网络中的函数逼近的强化学习算法实现。将策略评估表示为

31、<mstyle displaystyle="true" mathcolor="#000000"><mstyle displaystyle="true" mathcolor="#000000"><mover accent="true"><mi>w</mi><mo>^</mo></mover></mstyle><mstyle displaystyle="true" mathcolor="#000000"><munderover><mi /><mstyle displaystyle="true" mathcolor="#000000"><mi>c</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>t</mi></mstyle></munderover></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mo>[</mo><mstyle displaystyle="true" mathcolor="#000000"><mstyle displaystyle="true" mathcolor="#000000"><mi>φ</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mo>(</mo><mstyle displaystyle="true" mathcolor="#000000"><mstyle displaystyle="true" mathcolor="#000000"><mi>x</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>(</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>t</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>)</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>,</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mover accent="true"><mi>w</mi><mo>^</mo></mover></mstyle><mstyle displaystyle="true" mathcolor="#000000"><munderover><mi /><mstyle displaystyle="true" mathcolor="#000000"><mi>a</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>t</mi></mstyle></munderover></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>ψ</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>(</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>x</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>(</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>t</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>)</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>)</mi></mstyle></mstyle><mo>)</mo></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>−</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>φ</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>(</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>x</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>(</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>t</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>−</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>t</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><msub><mrow /><mi>s</mi></msub></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>)</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>,</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>u</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>(</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>t</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>−</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>t</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><msub><mrow /><mi>s</mi></msub></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>)</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>)</mi></mstyle></mstyle><mo>]</mo></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>=</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>−</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mstyle displaystyle="true"><msubsup><mo>∫</mo><mstyle displaystyle="true" mathcolor="#000000"><mstyle displaystyle="true" mathcolor="#000000"><mi>t</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>−</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>t</mi></mstyle></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mstyle displaystyle="true" mathcolor="#000000"><mi>t</mi></mstyle></mstyle></msubsup><mstyle displaystyle="true" mathcolor="#000000"><mstyle displaystyle="true" mathcolor="#000000"><mi>r</mi></mstyle></mstyle></mstyle></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>(</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>x</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>(</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>τ</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>)</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>,</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>u</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>(</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>τ</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>)</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>)</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>d</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>τ</mi></mstyle></mstyle>(9)

32、式中：ts表示每次迭代的时间间隔。和表示上一时刻的状态量和控制量，表示上一时刻的基函数，表示ts时间间隔内的评论家网络策略评估效果。表示连续可微且正定的实值函数。可采用递推最小二乘法或批量最小二乘法更新公式（8）中的动作-价值函数的参数。

33、基于策略迭代的思想，采用梯度下降法对演员网络参数进行更新：

34、(10)

35、式中，σ为待设计的正参数，表示当前第i时刻的演员神经网络估计值，表示当前时刻的评论家神经网络权重，是演员网络的基向量，表示当前第i时刻的演员神经网络关于控制量u的梯度信息。

36、特别地，迭代的时间间隔ts的值可以根据从观测中接收有意义的信息需要多长时间来改变。为此，定义演员网络数据三维存储栈，其具有la行、4列、以及最大页数；定义评论家数据二维堆栈，其具有行、以及最大列数。其中，对于当前序列，具有和。

37、设计基于数据堆栈的两步更新策略：

38、(11)

39、式中：将第列的最新栈定义为和<mstyle displaystyle="true" mathcolor="#000000"><mstyle displaystyle="true" mathcolor="#000000"><mi></mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><msub><mrow /><mrow><mstyle displaystyle="true" mathcolor="#000000"><mi>i</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>i</mi></mstyle></mrow></msub></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mo>(</mo><mstyle displaystyle="true" mathcolor="#000000"><mstyle displaystyle="true" mathcolor="#000000"><mi>:</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>,</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>ι</mi></mstyle></mstyle><mo>)</mo></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>=</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mo>[</mo><mrow><mstyle displaystyle="true" mathcolor="#000000"><mi>ψ</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><msup><mrow /><mi>∗</mi></msup></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>,</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mover accent="true"><mi>w</mi><mo>^</mo></mover></mstyle><mstyle displaystyle="true" mathcolor="#000000"><munderover><mi /><mi>c</mi><mrow><mi>∗</mi><mi>t</mi></mrow></munderover></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>,</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>φ</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><msup><mrow /><mi>∗</mi></msup></mstyle></mrow><mo>]</mo></mstyle><mstyle displaystyle="true" mathcolor="#000000"><msup><mrow /><mi>t</mi></msup></mstyle></mstyle>，其中和表示演员网络数据存储栈和评论家数据堆栈的最新数值。表示最小奇异值，其大小可通过奇异值分解方式计算得到。定义当前时刻为，对应的下一时刻为。由于在线数据堆栈的最大维度为，每个维度下的数值大小各不相同。定义为最大数值堆栈对应的时刻，使用最新飞行数据的目标列对进行更新，并满足表示在所取得的值域范围内的最大值。ηa是一个待设计的正常数。

40、对于公式（8）得到的控制量，为方便稳定性证明，定义第i个时刻产生的控制策略，存在实值函数满足连续可微分且正定，因此值函数满足如下关系

41、     (12)

42、其中，为第i个时刻对应的动力学关系。存在正常数，使得。

43、选取值函数为李雅普诺夫函数，基于公式（12），对求导可得

44、(13)

45、因此，闭环系统的平衡点是渐近稳定的，这意味着控制策略是可行的。

46、本发明的有益效果：

47、本发明的技术优点在于：

48、1. 考虑到高超声速变形飞行器的高度非线性、强时变特性、强耦合特性和不确定性大的问题，通过设计弱模型依赖智能控制方法降低控制方法对模型的依赖程度，以提高对模型不确定性的适应性，增强对不同气动外形的通用性，从根本上解决现有姿态控制方法与实际飞行任务需求之间的矛盾。

49、2. 通过设计基于数据堆栈的两步更新策略，应对变形阶段飞行控制造成飞行器系统数据传输压力大，以及执行机构频繁动作等问题，进一步强化了控制系统在线应用的可操作性。

50、3. 该方法适用于具有非仿射特征的高超声速变形飞行器控制需求，其动态非线性不仅依赖于系统的状态，而且依赖于控制输入，这对变形控制任务的实现至关重要。

51、本技术的关键点在于：

52、1. 基于弱模型依赖的控制方法，实现对飞行器模型不确定性的适应性，增强对不同气动外形的通用性。

53、2. 基于数据堆栈的两步更新策略，应对变形阶段飞行控制造成飞行器系统数据传输压力，以及执行机构频繁动作等问题，缓解在线频繁自适应更新带来的计算负担压力。

54、3. 采用积分强化学习作为智能控制方法，综合考虑飞行品质、控制性能和在线优化等多方面因素，同时具有设计简单、易于实现的特点。