一种基于复波数求解的粘弹性材料复杨氏模量测量方法

本发明涉及粘弹性材料的动态力学参数测量领域，具体的为一种基于复波数求解的粘弹性材料复杨氏模量测量方法。

背景技术：

1、粘弹性材料是一种介于弹性固体和粘性液体之间的特殊材料，同时表现出粘性和弹性，在减振降噪工程领域具有广泛的应用。准确测量粘弹性材料的复杨氏模量，对于材料的设计、选用以及性能分析具有重要的指导意义。

2、在粘弹性材料动态力学参数测量领域，目前粘弹性材料复杨氏模量常用的测量方法主要有两种思路:一种是通过测量样品的声学参数如声反射系数或声透射系数，再以此来反推材料力学参数，获得复杨氏模量；另一种是直接对样品施加激励，测量样品的振动响应计算出复杨氏模量。

3、其中，通过声学性能测试的方法测试结果不仅受声学参数测试结果的影响，还受反演模型的影响，需要使用在复平面搜根的方法来求解关于复纵波波数的超越方程，其计算复杂且准确度较低。

4、对样品施加激励，基于振动响应测量粘弹性材料复杨氏模量的测试方法主要包括：动态热机械分析法、强迫共振法、波速法、有限元反演法。

5、动态热机械分析法是在程序控制温度下，对样品施加交变应力，测试材料应变随着温度、时间的变化，进而获得材料复杨氏模量。该方法直接测试频率范围通常为0.01hz～100hz，即使是高频动态热机械分析仪也只能对1000hz以下频率范围进行测试，更高频范围内的复杨氏模量只能通过时温等效原理间接获得，而且操作复杂，设备昂贵。

6、强迫共振法利用一扫频信号对棒状样品进行激励，对纵向振动样品的自由端以及固定端的纵向振动响应进行测量，从而得到其自由端和固定端的振动幅度比曲线，继而通过共振时幅值比得到共振频率处的复杨氏模量。该方法只能在离散的共振频率点上进行有效测试，不能连续在宽频范围内测试。

7、有限元反演法通过对粘弹性材料进行有限元建模，输入参数为材料的弹性模量，通过将有限元计算得到的材料表面振动响应与实验测量结果对比，不断优化输入参数以使两者偏差满足误差条件，从而得到材料的复杨氏模量。该方法虽不受频率限制，但数学迭代计算量大，计算结果存在误差，且在某些条件下，反演计算模型无法收敛。

8、波速法利用单频信号对棒状样品进行纵向激励，利用两台激光测振仪对样品某位置处两侧面的横向振动分别进行测量，所测结果叠加后可消除弯曲振动的影响，得到因存在泊松比而由纵向振动引发的横向振动，对样品另一位置处的横向振动进行测量，继而通过两点振动响应的时延和衰减计算得到样品的复杨氏模量。该方法不限于样品共振频率，但是横向振动不易测量，且由于样品中反射信号的影响，测量频率不易太低。在中国发明专利cn107271301a中公开了一种在此基础上提出的基于直达波提取的波速法，消除了多次反射波叠加对测试的影响，并结合宽带脉冲技术拓宽了杨氏模量的准确测试频段，但仍然要依赖传统波速法分别计算储能模量和损耗因子，运算过程复杂。

技术实现思路

1、由于现有测量技术中，动态热机械分析法操作复杂、设备昂贵且在高频段等效拓展结果误差较大，强迫共振法的测量频率局限在离散频点处，有限元反演法存在迭代计算量大、模型无法收敛的情况，波速法需分别计算储能模量和损耗因子，运算过程复杂。本发明提出一种基于复波数求解的粘弹性材料复杨氏模量测量方法，通过与棒状样品中纵波传播相关中间变量的求解，能够直接得到复数杨氏模量，避免了分别求解储能模量和损耗因子的复杂过程，且同时得到了复波数k这一重要的材料参数。

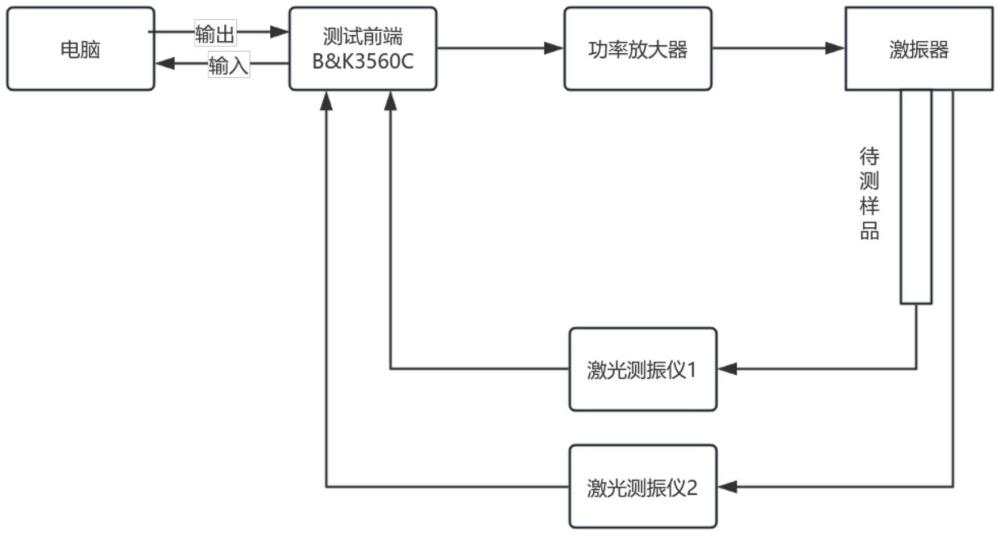
2、为实现上述目的，本发明提出一种基于复波数求解的粘弹性材料复杨氏模量测量方法，采用包括功率放大器、激振器、激光测振仪、信号发生和数据采集装置及安装配套软件的电脑等测量仪器。电脑控制发生装置发生信号经功率放大器放大后输入到激振器提供激励，采用激光测振仪对激振器及样品表面的振动信号进行测量并传递给数据采集装置进行记录存储，然后进行后续计算。具体测量步骤如下：

3、步骤1：将待测材料制成横截面为正方形的棒状样品，将样品一端竖直粘贴在激振器表面(称激振端)，另一端自由(称自由端)；

4、步骤2：采用信号发生装置发射时域宽频脉冲信号s(t)经功率放大器放大后发送到激振器，采用激光测振仪分别测量激振端和自由端纵向振动信号sd(t)和sf(t)，将获得的振动信号进行快速傅里叶变换得到频域信号sd(f)和sf(f)，即得到了样品激振端和自由端的频域振动响应，其中t为时间，f为频率；

5、步骤3：基于步骤2得到的样品激振端和自由端的频域振动响应求解与样品中纵波传播(复波数k)相关中间变量e-jkl，具体表达式为：

6、

7、式中，e-jkl为描述样品中纵波传播的无量纲量，k为样品材料的复波数，单位为m-1；j为虚数单位；l为样品长度，单位为m；

8、步骤4：根据步骤3获得的中间变量e-jkl求解复波数k，具体表达式为:

9、

10、式中，n为与复数运算多值问题相关的整数；

11、步骤5：基于步骤4获得的复波数k，计算得到复杨氏模量e*，具体表达式为:

12、

13、式中，e*表示复杨氏模量，单位为pa；f表示频率，单位hz；ρ为材料样品密度，单位为kg/m3。

14、进一步的，步骤1中，在样品自由端表面粘贴反光纸，提高样品反光性能，便于激光测振仪测量。

15、进一步的，步骤4中，n值的确定依据为：

16、(1)使得当傅里叶变换得的频率f趋近于0时候，复波数k趋近于0；

17、(2)使得复波数k为关于频率f的连续函数。

18、进一步的，步骤5中，用储能模量e′、损耗模量e″和损耗因子tanδ来表示测得的复杨氏模量具体如下：

19、e′＝real(e*)

20、e″＝imag(e*)

21、

22、式中，real(e*)表示复杨氏模量的实部，imag(e*)表示复杨氏模量的虚部。

23、有益效果

24、本发明提供一种基于复波数求解的粘弹性材料复杨氏模量测量方法，具有如下优点：

25、1、相比于动态热机械分析法，本发明不需要昂贵的实验设备，操作简单，而且能够实现宽频范围内的直接测试；

26、2、相比于强迫共振法，本发明采用宽频脉冲信号测试，无需寻找共振点，克服了对测量频率的限制，可以实现一次性测得样品宽频范围的复杨氏模量；

27、3、相比于有限元反演法，本发明不用迭代，不存在迭代计算量大、无法收敛的情况；

28、4、相比于波速法，本发明基于求解与样品中纵波传播(复波数k)相关中间变量e-jkl，通过复数运算直接得到样品材料的复波数及复数杨氏模量，较波速法分别求解储能模量和损耗因子更加快捷。

29、5、相比于声学测试方法，本发明直接通过力学响应进行测试，避免了反演过程中使用复平面搜根的方法来求解超越方程，而且克服了在低频范围内声学参数测试困难的问题。