一种基于极化码的紧凑格密钥交换和格公钥加密方法

本发明涉及密码学技术和信息安全，尤其涉及一种基于极化码的紧凑格密钥交换和格公钥加密方法。

背景技术：

1、密钥交换协议允许通信双方通过公共信道交换一些信息后，协商出相同的会话密钥，用于后续的加密等计算。首个著名的dh密钥交换协议是diffie与hellman于1976年提出的(diffie w,hellman m.new directions in cryptography[j].ieee transactions oninformation theory,1976,22(6):644-654.)，该协议通过两轮交互即可完成会话密钥的协商，成为了公钥密码学的基础构造。许多实用的公钥密码体制的安全性大都依赖于数学中的某些难解问题，目前广泛使用的两类公钥密码体制：rsa体制(rivest r l,shamir a,adleman l.a method for obtaining digital signatures and public-keycryptosystems[j].communications of the acm,1978,21(2):120-126.)及其变种和elgamal体制(elgamal t.a public key cryptosystem and a signature scheme basedon discrete logarithms[j].ieee transactions on information theory,1985,31(4):469-472.)及其变种，其安全性分别基于大整数分解问题和离散对数问题。但1994年shor证明了在量子计算模型下可以在多项式时间内破解上述经典数论问题(shor pw.algorithms for quantum computation:discrete logarithms and factoring[c]//proceedings 35th annual symposium on foundations of computer science.ieee,1994:124-134.)，因此寻找抗量子攻击的密码算法的构造变得极为重要。后量子密码算法有基于编码的密码、基于多变量的密码、基于格的密码以及基于同源的密码等，其中基于格的公钥密码算法的公钥尺寸更小，并且安全性和计算速度等指标更优，被认为是公钥加密算法最具潜力的替代者。

2、格密码的安全性可以归约为最坏情况下的困难问题假设，ajtai给出了证明表示格上最坏情况下的困难问题与平均情况下的困难问题是等价的(ajtai m,dwork c.apublic-key cryptosystem with worst-case/average-case equivalence[c]//proceedings of the twenty-ninth annual acm symposium on theory ofcomputing.1997:284-293.)。learning with errors(lwe)问题是格密码安全的重要保障，regev证明了求解一般情况下的lwe问题与求解最坏情况下的困难格问题一样困难(regevo.on lattices,learning with errors,random linear codes,and cryptography[j].journal of the acm(jacm),2009,56(6):1-40.)。但是，这些基于lwe问题的密码算法都要使用较大尺寸的矩阵参与构造，使得计算运行速度受限。为了进一步提高计算效率，lyubashevsky等人提出了ring learning with errors(rlwe)问题，将计算引入到多项式环上。同时，他们还给出了rlwe问题的安全性证明，证明了想要求解rlwe问题就要解出最坏情况下理想格上的困难svp问题(lyubashevsky v,peikert c,regev o.on ideallattices and learning with errors over rings[c]//annual internationalconference on the theory and applications of cryptographictechniques.springer,berlin,heidelberg,2010:1-23.)。在困难性保证下，许多基于格的公钥加密算法(gentry c,peikert c,vaikuntanathan v.trapdoors for hard latticesand new cryptographic constructions[c]//proceedings of the fortieth annualacm symposium on theory of computing.2008:197-206.lindner r,peikert c.betterkey sizes(and attacks)for lwe-based encryption[c]//cryptographers’track atthe rsa conference.springer,berlin,heidelberg,2011:319-339.)被提出。在密钥交换领域，基于格的密钥交换协议在安全性与计算效率上都有着较为优秀的表现。ding等人于2012年给出了分别在lwe问题与rlwe问题下的简单高效的密钥交换协议(ding j,xie x,lin x.a simple provably secure key exchange scheme based on the learning witherrors problem[j].cryptology eprint archive,2012.)。他们在协议中构造了robustextractor用于通信双方在近似相等的消息上达成确定性共识，使用误差同步(errorreciliation)技术设计了首个diffie-hellman式的密钥交换协议。2014年，peikert等人提出另一种误差同步技术，他们根据多项式环中模数的奇偶性不同采取不同处理的处理方式，最终得到一种相对简单且带宽更低的基于rlwe的认证性密钥交换协议(peikertc.lattice cryptography for the internet[c]//international workshop on post-quantum cryptography.springer,cham,2014:197-219.)。2016年，alkim等人通过对peikert等人的误差同步技术扩展应用，设计了一个基于rlwe问题的密钥交换协议，即newhope密钥交换协议(alkim e,ducas l,t,et al.post-quantum keyexchange—a new hope[c]//25th usenix security symposium(usenix security 16).2016:327-343.)。同年，alkim等人提出了newhope协议的变种newhope-simple(alkim e,ducas l,t,et al.newhope without reconciliation[j].cryptologyeprint archive,2016.)，该协议实际上是个加密算法，可以实现密钥交换的功能，用纠错码实现误差同步。在无线通信物理层安全领域，张孝甜等人针对无线信道特征密钥提取技术中获得的信道特征不完全一致的问题,提出了一种基于polar码的逆向密钥协商方案(张孝甜,赵生妹,郑宝玉.无线信道中的polar码协商[j].journal of signal processing,2018,34(7).)。但是该方法需要发送方alice得到接收方bob传输的冻结比特后进行polar码译码后再进行polar重编码，产生传输冻结比特带来的信息泄露。

技术实现思路

1、针对现有技术中存在的问题，本发明的目的在于一种基于极化码的紧凑格密钥交换和格公钥加密方法，本发明通过利用极化码的极化特性，与基于rlwe问题的密钥交换和公钥加密相结合，构造一种紧凑的格密钥交换方法和新的格公钥加密方法。

2、本发明的技术方法如下：

3、一种基于极化码的紧凑格密钥交换方法，适用于合法通信双方alice与bob，所述方法包括如下步骤：

4、1)发送方alice与接收方bob基于rlwe的密钥交换协议思想构造本发明的密钥协商协议，生成近似一致的初始密钥ka和kb；

5、2)通信双方利用ding等人的误差同步技术调制初始密钥ka和kb，纠正初始密钥中一部分不一致的比特序列，得到和

6、3)利用极化码的极化性质，产生基于rlwe的密钥交换协议中通信双方共享的会话密钥ska,skb。即bob对进行polar码逆编码，并将冻结比特传输给alice；alice获得冻结比特及其位置信息后，进行polar译码，对进行纠错；最后双方将信息比特位置的值作为双方共享的会话密钥ska,skb。

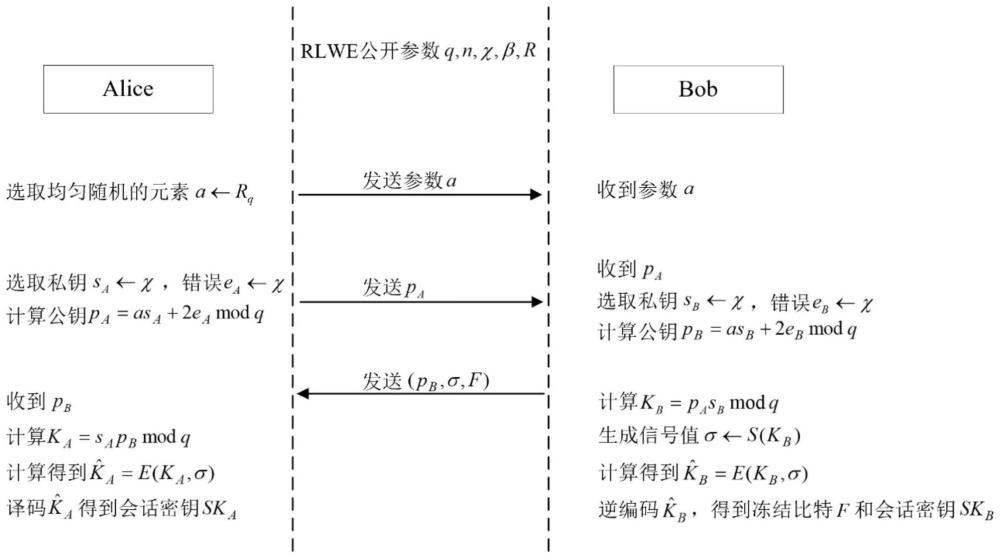
7、进一步地，所述发送方alice与接收方bob基于rlwe的密钥交换协议思想构造本发明的密钥协商协议，生成近似一致的初始密钥ka和kb，包括：

8、1)通信双方得到公开参数其中，q为多项式环rq的模数，n为模多项式的次数，为误差分布，通常可以选择高斯分布或中心二项分布，β为误差分布的上界，a为从多项式环rq中均匀随机选取的元素。多项式环即rq中的任一多项式m可以表示成形式，其中x表示多项式环rq中多项式的未定元，为第i个多项式系数，表示多项式环rq中的系数取自模q整数环是模q整数环，中的元素是一个取值为0～q-1的整数；是模q多项式环，系数为0～q-1的多项式；是多项式环，系数为整数的多项式；

9、2)alice根据误差分布从误差分布的取值集合中随机选取元素sa、ea，即选取私钥错误计算rlwe形式的公钥pa＝asa+2eamod q，并发送公钥pa给bob；

10、3)bob收到来自alice的公钥pa，也类似地计算自己的公钥，首先选取私钥错误计算pb＝asb+2ebmod q，并将公钥pb发送给alice；

11、4)bob利用类diffie-hellman思想计算kb＝pasbmodq；

12、5)alice收到来自bob的公钥pb，利用类diffie-hellman思想计算ka＝sapbmod q。

13、进一步地，所述通信双方利用ding等人的误差同步技术调制初始密钥，包括：

14、关于signal函数，对于rq上的输入有

15、s(c)＝σb(c),其中b←{0,1}，s(c)以1/2概率等于σ0(c)，以1/2概率等于σ1(c)；

16、其中，signal(c)简写为s(c)，s(c)即为输入c对应的信号signal，c为rq中的多项式，ci为c的第i个系数，i的取值为0到n-1。

17、关于σb(c)，对于rq上的输入有rq→r2的变换：

18、

19、其中关于σ0(ci),σ1(ci)，对于输入有的变换：

20、

21、关于误差消除函数e，对于rq上的输入以及与c对应的信号值σ，有

22、

23、信号值σ是n长的0/1比特串，信号值σ为上述的σ0(c)或σ1(c)。

24、bob利用signal函数对多项式环rq上的kb计算信号值σ＝s(kb)，并将信号值σ发送给alice；

25、bob根据信号值σ与误差消除函数e，计算

26、alice收到来自bob的信号值σ，对初始密钥ka进行相应调制，即

27、进一步地，所述利用极化码的极化性质，产生基于rlwe的密钥交换协议中通信双方共享的会话密钥ska,skb，包括：

28、1)通信双方alice和bob根据公开信道特征，设计并构造极化码，根据极化码的构造特点，alice和bob共享信息位集合(放信息比特，即会话密钥)和冻结位集合(放冻结比特)；

29、2)bob将看成极化码的码字，逆编码后会得到极化码的冻结比特f和会话密钥skb，将冻结比特f发送给alice；

30、3)alice接收到冻结比特f后，译码得到会话密钥ska。在极化码纠错范围内，ska＝skb。

31、进一步地，由于本发明把共享密钥的生成过程转移到了多项式环上，例如在pa＝asa+2eamod q的计算中，asa为rq上的多项式模乘操作。所以，在协议执行过程中关于多项式的乘法计算，可以利用ntt算法进行加速，使得计算复杂度从原始的o(n2)降低到o(n log n)，极大提高了协议的运行速度，降低了资源消耗。

32、进一步地，在实现时本发明可以利用较新的硬件构造——计算和存储一体化(process-in-memory)单元进行数据计算，将数据计算合并到数据存储过程中，从而省去了传统计算过程中频繁的数据读取与存储过程，可以大幅度降低功耗、提升速率。存算一体结构由于在存储单元内进行计算，避免了频繁的数据搬移/读取，可以减少数据搬移过程中高达90％的功耗成本，从而提升计算能效比。同时，该架构也减少了等待数据读取时算力的浪费。在该架构下，想要提升算力只需增加“存算一体单元”的个数，工程上更简洁。

33、一种基于极化码的格公钥加密方法，适用于合法通信双方alice与bob，所述方法包括如下步骤：

34、1)密钥生成：执行上述一种基于极化码的紧凑格密钥交换方法，产生基于rlwe的密钥交换协议中通信双方共享的会话密钥ska,skb；

35、2)加密：bob选取消息m←r2，计算发送给alice；多项式环r2的系数为模2整数环即消息m的系数是0或1，方便与会话密钥进行异或操作，即

36、3)解密：alice计算得到消息m。

37、与现有技术相比，本发明具有以下优点：

38、1)本发明的基于极化码的格密钥交换方法利用极化码的极化性质，纠正基于格的密钥交换协议中初始密钥中不一致的比特。与只使用误差同步的技术相比，本方法的模数较小；与使用其他纠错码的方法相比，本方法的通信量较少，更紧凑。

39、2)本发明利用极化码的极化性质，提出了一种新的基于极化码的格公钥加密方法。

40、3)由于本发明把共享密钥的生成过程转移到了分圆域上，所以对于多项式模乘，本发明利用ntt算法对其进行加速，相比于传统的模乘计算大幅度地节约了运行时间。

41、4)可以利用计算和存储一体化(process-in-memory)架构，将数据计算合并到数据存储过程中，大大提高会话密钥的生成速度。