一种基于多级模糊评价模型的数据挖掘方法与流程

本发明涉及电力系统故障检测，尤其涉及一种基于多级模糊评价模型的数据挖掘方法。

背景技术：

1、随着电力系统的复杂性和规模的不断增加，电力系统的运行和维护面临着越来越多的挑战。传统的故障检测方法通常依赖于固定阈值和经验规则，这些方法在面对复杂多变的电力系统环境时往往表现出不足，无法及时、准确地检测和定位故障。同时，随着智能电网和大数据技术的发展，如何有效地利用海量数据进行故障检测和诊断成为一个重要的研究方向。模糊逻辑和贝叶斯网络作为处理不确定性和模糊性的有效工具，在电力系统故障检测中展现出了巨大的潜力。

技术实现思路

1、鉴于上述现有存在的问题，提出了本发明。

2、因此，本发明提供了一种基于多级模糊评价模型的数据挖掘方法，能够解决传统方法忽略了数据间的模糊性和不确定性，无法有效处理复杂数据的问题。

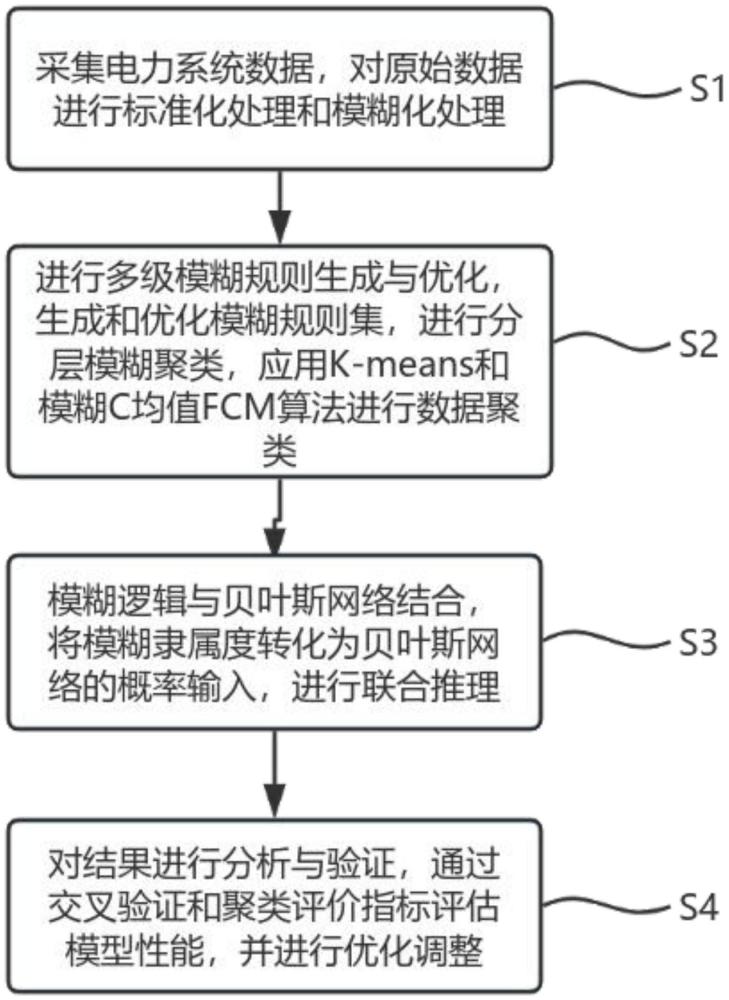
3、为解决上述技术问题，本发明提供如下技术方案，一种基于多级模糊评价模型的数据挖掘方法，包括：

4、采集电力系统数据，对原始数据进行标准化处理和模糊化处理；进行多级模糊规则生成与优化，生成和优化模糊规则集，进行分层模糊聚类，应用k-means和模糊c均值fcm算法进行数据聚类；模糊逻辑与贝叶斯网络结合，将模糊隶属度转化为贝叶斯网络的概率输入，进行联合推理；对结果进行分析与验证，通过交叉验证和聚类评价指标评估模型性能，并进行优化调整。

5、作为本发明所述的基于多级模糊评价模型的数据挖掘方法的一种优选方案，其中：所述对原始数据进行标准化处理和模糊化处理包括，对原始数据进行标准化处理，消除不同维度之间的尺度差异，使用模糊隶属函数对数据进行模糊化处理，得到每个数据点的模糊隶属度。

6、作为本发明所述的基于多级模糊评价模型的数据挖掘方法的一种优选方案，其中：所述对原始数据进行标准化处理和模糊化处理还包括，选用高斯隶属函数进行模糊化处理，通过数据统计分析方法获取数据的均值μ和标准差σ，隶属度μ(x)的高斯函数形式为：

7、

8、引入数据集中的每个数据点xi，构建分式表达式，同时使用拉普拉斯变换和卷积运算进行运算，具体如下：

9、

10、其中，表示拉普拉斯变换作用于两个函数f(t)和g(t)的卷积结果；f(t)＝sin(t)和g(t)＝e-t2分别是两个选用的函数；xi为数据集中的第i个数据点，μi为数据集中第i个数据点的均值，σi为数据集中第i个数据点的标准差，μ(xi)为数据点xi的模糊隶属度；t为卷积和拉普拉斯变换中的时间变量；n为数据集中数据点的总数；

11、隶属度μ(xi)的值域为[0,1]，其中0表示数据点完全不属于某一模糊集合，1表示数据点完全属于某一模糊集合，中间值表示存在部分隶属关系。

12、作为本发明所述的基于多级模糊评价模型的数据挖掘方法的一种优选方案，其中：所述对原始数据进行标准化处理和模糊化处理还包括，对拉普拉斯变换进行展开，拉普拉斯变换定义为:

13、

14、对于卷积f(t)*g(t)，其定义为:

15、

16、因此，卷积的拉普拉斯变换为:

17、

18、根据拉普拉斯变换的卷积定理：

19、

20、设定f(t)＝sin(t)和g(t)＝e-t2，分别计算这两个函数的拉普拉斯变换:

21、拉普拉斯变换f(t)＝sin(t)：

22、

23、拉普拉斯变换

24、

25、使用误差函数erf(t)的形式进行计算，具体结果为:

26、

27、组合拉普拉斯变换结果：

28、

29、代入原公式获得：

30、

31、其中，erf为误差函数。

32、作为本发明所述的基于多级模糊评价模型的数据挖掘方法的一种优选方案，其中：所述多级模糊规则生成与优化包括，采用遗传算法或粒子群优化算法，自动生成适用于多级模糊评价模型的模糊规则集；

33、选用基于均方误差mse的适应度函数评估每个模糊规则集的性能，使用编码表示每个模糊规则集，将每个规则集的参数进行编码，形成个体；

34、定义适应度函数f为：

35、

36、其中，yi是实际值，f(xi；θ)是模型预测值，θ是模型参数；

37、通过交叉和变异操作生成新的个体，定义交叉概率和变异概率控制操作的频率定义粒子的位置和速度更新公式，结合模糊规则集的参数进行优化，具体如下：

38、θt+1＝θt+ωvt+c1r1(θpbest-θt)+c2r2(θgbest-θt

39、其中，

40、vt+1＝ωvt+c1r1(θpbest-θt)+c2r2(θgbest-θt)

41、θt表示当前粒子的位置，也即当前模糊规则集的参数；vt表示当前粒子的速度，ω是惯性权重，c1和c2是加速常数，r1和r2是随机数，θpbest和θgbest分别是粒子的历史最佳位置和全局最佳位置。

42、作为本发明所述的基于多级模糊评价模型的数据挖掘方法的一种优选方案，其中：所述分层模糊聚类包括，在数据的不同层级上应用k-means聚类算法进行初步聚类，得到初步聚类中心，以k-means聚类的中心为初始点，应用模糊c均值fcm算法进行模糊聚类，得到每个数据点的模糊隶属度，并将各层级的模糊聚类结果进行融合，形成整体的模糊聚类结果；

43、对数据集进行初步聚类，得到初步聚类中心

44、以μj作为初始聚类中心，进行模糊聚类，得到每个数据点的模糊隶属度uij；

45、综合k-means和fcm的计算步骤，进行初始化:

46、

47、模糊隶属度更新:

48、聚类中心更新：

49、停止条件:

50、其中，为第j个初始聚类中心,由k-means算法得到；xi为第i个数据点；n为数据点的总数；k为聚类的个数；为第i个数据点在第t次迭代时对第j个聚类的隶属度；m为隶属度的模糊因子,取值大于1；∥·∥为欧氏距离；∈为停止条件的阈值,常设为10-5或10-6；为第j个聚类中心在第t次迭代时的值；为第j个聚类中心在第t+1次迭代时的值。

51、作为本发明所述的基于多级模糊评价模型的数据挖掘方法的一种优选方案，其中：所述模糊逻辑与贝叶斯网络结合包括将模糊隶属度转化为贝叶斯网络的概率输入，并通过贝叶斯网络的联合推理机制进行推理和决策；

52、使用模糊隶属度转化为贝叶斯网络的条件概率,构建贝叶斯网络，通过条件概率进行联合推理，计算目标事件的概率，具体如下：

53、

54、贝叶斯网络的联合概率分布表示为:

55、

56、其中，p(xi∣y)是基于模糊隶属度转化得到的条件概率；

57、

58、uij为第i个监测点数据对第j个故障类型的模糊隶属度，表示数据点的故障类型的程度；p(aj∣xi)为第i个监测点数据属于第j个故障类型的条件概率，表示在给定监测点数据xi下，发生故障类型aj的概率；k为故障类型的总数，表示电力系统中可能的故障类别总数；p(y∣x)为在给定所有监测点数据集合x时，目标故障事件y发生的概率；p(y)为目标故障事件y的先验概率，表示在没有任何监测数据时，故障y发生的概率；p(xi∣y)为在目标故障事件y发生时，第i个监测点数据xi的条件概率，表示在故障y发生的前提下，观测到xi的可能性；n为监测点的总数，表示电力系统中布置的监测设备或传感器的数量；x为所有监测点数据的集合，包含{x1,x2,…,xn}；y为目标故障事件，表示电力系统中某一具体的故障类型；τ为预设决策阈值，设定在0到1之间；决策结果中，1表示检测到故障，0表示未检测到故障。

59、作为本发明所述的基于多级模糊评价模型的数据挖掘方法的一种优选方案，其中：所述结果分析包括通过交叉验证或留出验证法评估多级模糊评价模型的性能，并采用聚类评价指标对聚类效果进行评价；

60、分割数据集进行训练和测试，通过多次验证评估模型性能；

61、模糊分割系数fpc：

62、

63、模糊熵fe：

64、

65、综合评价模型性能的公式如下：

66、score＝α·fpc-β·fe

67、其中，k为交叉验证的折数，表示将数据集分成的子集数量；n为数据点的总数，表示数据集中的样本数量；uij为第i个数据点对第j个聚类的模糊隶属度，表示数据点属于某聚类的程度；fpc为模糊分割系数，衡量数据点隶属于聚类的程度，数值越高表示聚类效果越好；fe为模糊熵，衡量数据点隶属于聚类的不确定性，数值越低表示聚类效果越好；α为模糊分割系数的权重系数，表示指标在综合评价中的重要程度；β为模糊熵的权重系数，表示指标在综合评价中的重要程度；score为综合评价得分，表示模型的整体性能。

68、一种计算机设备，包括存储器和处理器，所述存储器存储有计算机程序，其特征在于，所述处理器执行所述计算机程序时实现基于多级模糊评价模型的数据挖掘方法的步骤。

69、一种计算机可读存储介质，其上存储有计算机程序，其特征在于，所述计算机程序被处理器执行时实现基于多级模糊评价模型的数据挖掘方法的步骤。

70、本发明的有益效果：本发明提供了一种基于多级模糊评价模型的数据挖掘方法，通过结合模糊逻辑和贝叶斯网络的优势，解决了现有技术的缺陷。具体而言，本发明采用模糊隶属函数对数据进行模糊化处理，得到每个数据点的模糊隶属度，并将其转化为贝叶斯网络的概率输入，通过贝叶斯网络的联合推理机制进行推理和决策。此外，本发明通过交叉验证或留出验证法评估模型的性能，并采用模糊分割系数和模糊熵等聚类评价指标对聚类效果进行综合评价。该方法不仅提高了故障检测的准确性和灵活性，而且能够全面评估模型性能，为电力系统的安全稳定运行提供了有力保障。