基于再分析资料考虑大气稳定度影响的风速垂直外推方法与流程

本发明涉及风力发电，具体涉及基于再分析资料考虑大气稳定度影响的风速垂直外推方法。

背景技术：

1、风资源评估在风电场建设中具有举足轻重的地位，它直接关系到风电场的年产能预测、风电机组场址的适应性评估以及风电项目的整体经济效益。在这一过程中，测风塔获取的风速数据的代表性成为了评估结果准确性的关键因素。然而，现实情况中，测风塔的数量往往有限，且其测量高度也受到一定限制，这给准确评估风资源带来了挑战。

2、风资源评估是风电场选址、设计、建设和运营的基础。通过对某一区域的风速、风向、气温、气压等气象参数的观测和分析，可以估算出该区域的风能资源储量，进而为风电场的布局、风电机组的选型以及发电量预测提供科学依据。准确的风资源评估有助于避免投资风险，提高风电场的经济效益和社会效益。

3、在风资源评估中，测风塔获取的风速数据是评估工作的重要依据。然而，由于测风塔数量有限且测量高度受限，其数据的代表性成为了影响评估结果准确性的主要因素。具体来说，测风塔的数据可能无法全面反映整个风电场区域的风速分布情况，特别是在地形复杂、风速变化较大的区域。此外，随着风机技术的发展，风电风轮直径和轮毂高度不断增加，对轮毂高度处风速数据的准确性要求也越来越高。

4、为了解决低高度处测风数据无法直接代表轮毂高度处风速的问题，工程上常采用风速垂直外推模型。其中，指数模型是一种广泛使用的经验模型。该模型通过一定的数学关系将低高度处的风速数据外推至轮毂高度处。

5、然而，这种方法在实际应用中存在一些问题：

6、模型参数的选取：指数模型的准确性很大程度上取决于模型参数的选取。然而，在实际应用中，由于地表粗糙程度、大气稳定度等因素的复杂性，很难准确确定模型参数。工程上往往采用简化的方法直接取值这会导致外推风速的准确性降低。

7、风速廓线的变化：风速廓线随大气稳定度的变化而变化。在白天和夜间、晴天和阴天等不同条件下，风速廓线的形状和斜率会有所不同。然而，传统的风速垂直外推模型往往忽略了这一点，导致外推的风速存在系统性误差。

技术实现思路

1、针对现有技术存在的不足，本发明提出一种基于再分析资料考虑大气稳定度影响的风速垂直外推方法，以解决现有技术中存在的的技术问题。

2、本发明采用的技术方案：

3、提供了基于再分析资料考虑大气稳定度影响的风速垂直外推方法，包括：

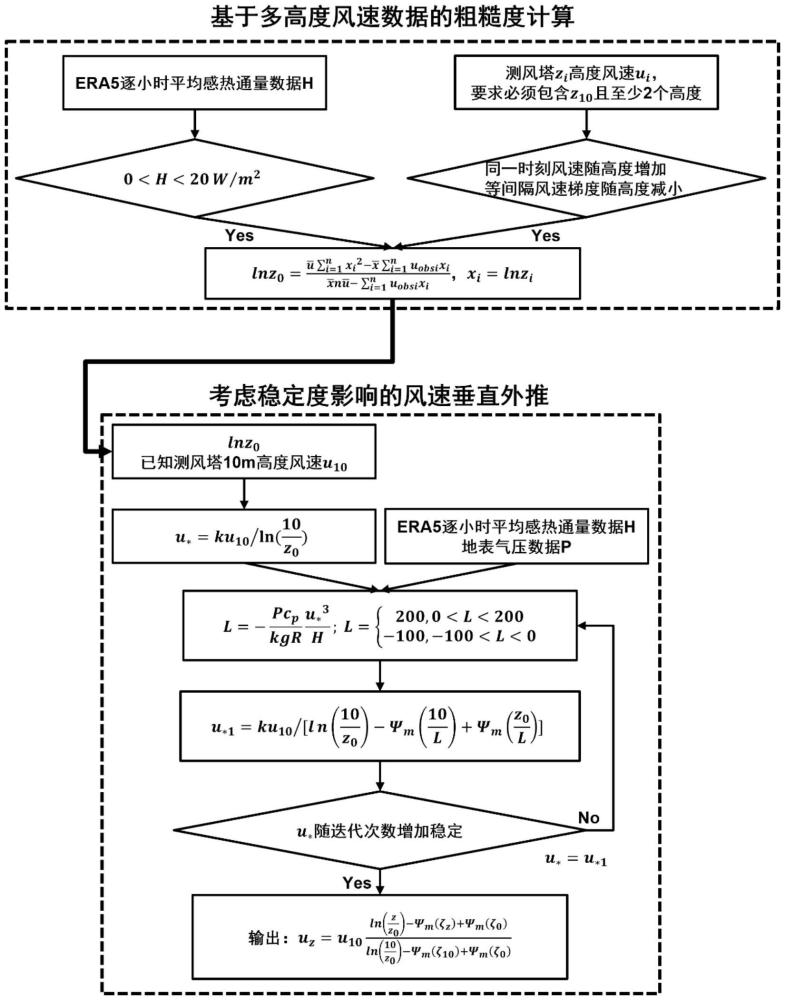
4、基于monin–obukhov相似理论，得到基于测风塔多高度风速计算的粗糙度解析表达式；

5、基于大气再分析资料判断稳定度和obukhovlength约束，实现风速垂直廓线的高精度外推，包括：

6、基于粗糙度解析表达式得到测风塔的粗糙度，结合测风塔10m高度风速u10计算中性条件下的测风塔的摩擦速度，作为摩擦速度的初值；

7、基于得到的摩擦速度初值和再分析资料提供的逐小时平均的感热通量数据h和逐小时地表气压p，计算得到obukhovlength，从而确定稳定度修正项；

8、基于计算得到的稳定度修正项，迭代求解不同稳定度条件下的风廓线方程直到摩擦速度稳定，基于稳定的摩擦速度，计算近地层任一高度风速。

9、进一步的，基于monin–obukhov相似理论，得到基于测风塔多高度风速计算的粗糙度解析表达式，并在粗糙度计算之前要求：

10、获取测风塔在不同高度点的风速数据、逐小时平均的感热通量数据h；

11、将获取测风塔在不同高度点的风速数据进行质量控制；

12、确保获取的每小时平均的感热通量数据h，满足大气处于中性的条件。

13、进一步的，获取的风速数据至少包括两个不同高度点的风速数据且至少有一个高度点为10m。

14、进一步的，所述质量控制包括：控制测风塔风速数据在同一时刻风速随高度增加，且等间隔风速梯度随高度减小。

15、进一步的，所述感热通量在0-20w/m2范围时，满足大气处于中性的条件。

16、进一步的，所述基于monin–obukhov相似理论，得到基于测风塔多高度风速计算的粗糙度解析表达式，具体为：

17、基于monin–obukhov相似理论，中性条件下z高度的风速u表示为：

18、

19、其中，k为vonkarman常数，u*为摩擦速度，z0为空气动力学粗糙度；

20、其中，

21、

22、令lnz0＝x0，lnz＝x，则：

23、

24、同一时刻的u*保持不变：

25、

26、其中，为所有高度的平均风速，为所有高度的x的平均高度；

27、将u*带入到对数廓线中，zi高度处的风速ui为：

28、

29、基于zi高度处的计算风速ui和对应的测风塔实测风速uobsi，利用成本函数：

30、

31、推导得到包含多高度风速的粗糙度解析表达式为：

32、

33、其中，xi＝lnzi。

34、进一步的，所述结合测风塔10m高度风速u10计算中性条件下的测风塔的摩擦速度表达式为：

35、

36、进一步的，所述基于上述得到的摩擦速度初值和再分析资料提供的逐小时平均的感热通量数据h和逐小时地表气压p，计算得到obukhovlength，从而确定稳定度修正项，具体包括：

37、基于monin–obukhov相似理论，风速随高度的变化服从对数律公式：

38、

39、其中，k为von karman常数，u*为摩擦速度，z0为空气动力学粗糙度，ζ为稳定度参数，ψm为稳定度修正项；

40、稳定度修正项表示为：

41、

42、由风速随高度的变化服从对数律公式可知，稳定度修正项是稳定度参数的函数，其中l是obukhovlength，表达式为：

43、

44、其中，ρ为空气密度，cp为定压比热容，t0为温度，u*为摩擦速度，k为vonkarman常数，g为重力加速度，h为感热；

45、结合气体方程：

46、p＝ρrt0

47、其中，p为气压，ρ为空气密度，p为比气体常数，t0为温度；

48、得到：

49、

50、其中，k＝0.4；g＝9.8ms；cp＝1004j(kg·k)；r＝287j(kg·k)；稳定度参数在近地层的适用范围，在近地层顶z＝200m处：则在计算过程中进行如下控制：

51、

52、进一步的，利用泰勒级数，在中性条件下，指数模型中α表示为所述指数模型中α能通过所述多高度风速的粗糙度解析表达式得到。

53、进一步的，基于稳定的摩擦速度，通过计算近地层任一高度公式，计算近地层任一高度采用的风速，所述计算近地层任一高度公式表示为：

54、

55、由上述技术方案可知，本发明的有益技术效果如下：

56、1.本发明能在仅知低高度处风速时，可以外推得到近地层任一高度较准确的风速。

57、2.本发明计算出的粗糙度改进后的指数模型，能有效降低外推风速平均绝对偏差百分比。

58、3.本发明能降低测风塔测风成本。测风塔造价昂贵，多年长期的多高度测风需要较高成本。该发明允许测风塔只进行短期的多高度观测，该时段数据用于当地粗糙度的计算，之后只需进行10m高度的风速观测，就可以获得测风塔所在位置的轮毂高度处的风速数据。