一种基于粒子群算法的拉普拉斯极短弧定轨算法

本发明涉及航天器短弧定轨计算领域，特别是一种基于粒子群算法的拉普拉斯极短弧定轨算法。

背景技术：

1、天基探测卫星采用相机对空间目标进行观测时，以恒星为背景拍摄空间目标。由于恒星的方向是已知的，利用坐标量测仪测量空间目标和恒星在图像上的相对位置就可求得空间目标的方位信息。虽然能利用光学有效载荷探测空间目标获得测角量，无法获得探测器与碎片间的距离，且需要在较短的观测时间下的观测数据内对目标进行定轨编目，这对算法的输入提出了一定的要求，即在有限较少的观测方向中对目标进行极短弧定轨。

2、目前，定轨算法由于测站的多少(单一、多个)的不同、测量量的属性(位置、速度、角度)的差别相应地有不同的轨道确定方法。对于极短弧定轨而言，常见的有开普勒元素法，微分修正法，优化算法和扩展卡尔曼滤波算法。开普勒元素法虽然计算较快原理简单，但其精度较低，难以剔除异常值，而微分修正法和优化算法有着计算复杂度较高的缺点，扩展卡尔曼滤波算法则要求原有的动力学模型有较高的准确性。

3、因此亟需一种基于粒子群算法的拉普拉斯极短弧定轨算法来解决上述问题。

技术实现思路

1、为解决上述问题，本申请提供了一种基于粒子群算法的拉普拉斯极短弧定轨算法，以快速极短弧定轨为目标，旨在能够消除野值和残差的影响，进而达到精准定轨的目的。

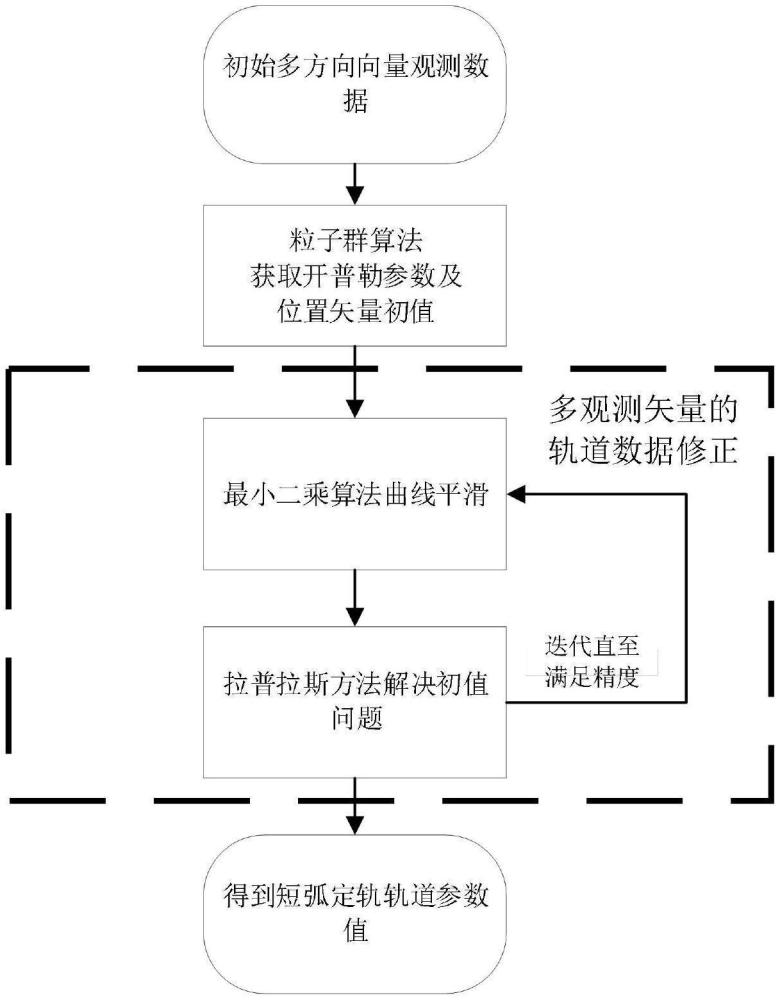
2、在本申请，提供了一种基于粒子群算法的拉普拉斯极短弧定轨算法，包括以下步骤：

3、s1、获取每一时刻观测卫星的坐标位置矢量及其观测所得的方向矢量，利用粒子群算法计算每一时刻方向矢量对应的开普勒参数初值(a,e,m)，及其在惯性系下所对应的目标位置矢量；

4、s2、利用拉普拉斯方法和最小二乘算法对s1中得到的每一时刻目标位置矢量进行定轨、修正并消除野值，计算短弧段所对应的轨道参数和各个时刻对应的真近角。

5、优选的，s1的具体步骤如下：

6、s101：获取开普勒参数范围内的三个变量得到粒子群算法变量并定义三个变量为开普勒参数的初始值(a,e,m)；

7、s102：根据开普勒参数值计算每一时刻的平近角及其所对应的真近角，根据平近角及其所对应的真近角计算目标的位置矢量模长；

8、s103：获取观测所得的方向矢量和观测卫星的坐标位置矢量并计算二者之间的夹角，得到目标卫星的位置矢量初始估计值；

9、s104：根据s103计得到的位置矢量初始估计值，计算粒子群算法所对应的目标适值函数，进行粒子群算法变量的更新；

10、s105：重复s101至s103的操作，进行迭代，得到优选目标适值函数值并将开普勒参数初值以及各个时刻位置矢量值进行输出。

11、优选的，步骤s102中，所述平近角和模长的计算表达式如下：

12、mi＝m0+n(ti-t0)；

13、|ri|＝a(1-ecosfi)；

14、其中，m为平近角值，n为轨道平均角速度，a为轨道半长轴值，e为离心率，r为目标位置矢量，为真近角，i为位置角标。

15、优选的，s103计算位置矢量值所用的表达式如下：

16、

17、ri＝ρi×nji+ri；

18、其中，ri为观测卫星在地心惯性系下的坐标矢量，nji为针对于目标观测所得的方向矢量，β为二者矢量的夹角，为开普勒参数下位置矢量的估计值，ρi为观测卫星至目标卫星的矢径模长估计值。

19、优选的，s104中目标适值函数的表达式如下：

20、

21、其中，r为计算的位置矢量，f为每一次迭代所对应的粒子群适应值，n为观测的时刻数。

22、优选的，s2的具体步骤如下：

23、s201：采用多项式曲线平滑拟合，对若干时刻位置矢量值进行修正；

24、s202：获取t0时刻的位置速度信息，计算得到轨道半长轴初值、平近角值、偏近角值、参数p和参数的初值；

25、s203：利用s202得到的数值，计算拉普拉斯函数值，并进行轨道外推，得到若干时刻的位置矢量值和速度矢量值；

26、s204：将若干时刻位置矢量值代入s201，重复s201至s203的内容，进行迭代计算，得到准确值和准确值；

27、s205：利用位置矢量和速度矢量值求得若干轨道根数并进行定轨。

28、优选的，s201中采用多项式曲线平滑拟合的具体内容为：

29、获取时刻的初始位置矢量以及速度向量

30、采用多项式拟合函数进行拟合；

31、多项式拟合函数的表达式为：

32、

33、其中，r为位置矢量值，t为时刻值，d为各个时刻的位置矢量，j为位置角标，

34、优选的，s203采用的拉普拉斯函数表达式为：

35、

36、其中，v为目标的速度，f、g、f、g为拉普拉斯算子。

37、优选的，s203中轨道外推表达式为如下：

38、

39、其中，a为轨道半长轴，r0为位置矢量模长值，v0为速度矢量模长值，p为拉普拉斯向量模长值。

40、优选的，s204中进行迭代计算过程中，当以及时，终止迭代。

41、综上所述，本发明的一种基于粒子群算法的拉普拉斯极短弧定轨算法，相比传统航天器短弧定轨计算技术，本算法由粒子群算法，轨道外推的拉普拉斯方法以及最小二乘算法组成，通过粒子群算法完成方向向量至开普勒常数以及每个时刻的位置信息的初步运算，在经过拉普拉斯方法和最小二乘方法对观测矢量的轨道数据修正，消除野值和残差的影响，二者之间相互迭代，得到较为精确的轨道参数值，对传统的粒子群算法定轨计算进行改进，提高了多矢量定轨计算的准确性，具有较好的适用性。

42、下面通过附图和实施例，对本发明的技术方案做进一步的详细描述。

技术特征：

1.一种基于粒子群算法的拉普拉斯极短弧定轨算法，其特征在于，包括以下步骤：

2.根据权利要求1所述的一种基于粒子群算法的拉普拉斯极短弧定轨算法，其特征在于，s1的具体步骤如下：

3.根据权利要求2所述的一种基于粒子群算法的拉普拉斯极短弧定轨算法，其特征在于，步骤s102中，所述平近角计算的表达式如下：

4.根据权利要求2所述的一种基于粒子群算法的拉普拉斯极短弧定轨算法，其特征在于，s103中目标卫星的位置矢量初始估计值计算所用的表达式如下：

5.根据权利要求2所述的一种基于粒子群算法的拉普拉斯极短弧定轨算法，其特征在于，s104中目标适值函数的表达式如下：

6.根据权利要求1所述的一种基于粒子群算法的拉普拉斯极短弧定轨算法，其特征在于，s2的具体步骤如下：

7.根据权利要求6所述的一种基于粒子群算法的拉普拉斯极短弧定轨算法，其特征在于，s201中采用多项式曲线平滑拟合的具体内容为：

8.根据权利要求6所述的一种基于粒子群算法的拉普拉斯极短弧定轨算法，其特征在于，s203中计算拉普拉斯函数值采用的拉普拉斯函数表达式为：

9.根据权利要求6所述的一种基于粒子群算法的拉普拉斯极短弧定轨算法，其特征在于，s203中轨道外推表达式为：

10.根据权利要求6所述的一种基于粒子群算法的拉普拉斯极短弧定轨算法，其特征在于，s204中的迭代计算过程中，当以及时，终止迭代。

技术总结本发明公开了一种基于粒子群算法的拉普拉斯极短弧定轨算法，涉及航天器短弧定轨计算领域，计算方法包括，获取每一时刻观测卫星的坐标位置矢量及其观测所得的方向矢量，利用粒子群算法计算每一时刻方向矢量对应的开普勒参数初值及其在惯性系下所对应的目标位置矢量，利用拉普拉斯方法和最小二乘算法对每一时刻目标位置矢量进行定轨、修正并消除野值，计算短弧段所对应的轨道参数和各个时刻对应的真近角，实现了对目标从方向向量到最后的轨道参数的定轨计算，抵消掉了观测时野值带来的偏差，可以快速极短弧定轨。技术研发人员：霍明英,马艺森,齐骥,李铮,范子琛,齐乃明受保护的技术使用者：哈尔滨工业大学技术研发日：技术公布日：2024/11/14