一种捷联惯组外场半系统级标定方法

本发明涉及惯性传感器标定，涉及一种中高精度捷联惯组外场半系统级标定方法。

背景技术：

1、作为惯性导航系统的核心部件，捷联惯组(simu，strapdown inertialmeasurement unit)在出厂之前必须进行实验室或厂级标定(内场标定)，标定误差参数包括惯性传感器(陀螺和加速度计)的标度因数、非正交误差、零偏误差等，甚至包括前述误差参数随温度的变化关系。在内场条件下，三轴精密转台、温度控制箱、离心机和测试工装夹具等惯性测试设备配备相对充分，可以对simu作细致标定和误差参数分离，获得高精度的标定结果。然而，在外场条件下，缺乏高精度测试设备，往往只能通过一些简单翻转角运动对simu主要标定参数的精度性能作复核或修正。

2、simu的标定方法有分立式标定和系统级标定，近年来，国内外专家学者在此基础上研发了一些方法，例如以陀螺转动为参考基准确定坐标系的系统级标定方法，需要准确的天向转动角度作为参考，但未彻底摆脱对转台设备的依赖；或以观测重力模值进行加速度计标定，利用levenberg-marquardt(lm)优化算法求解标定参数，但主要用于低精度simu。本发明提出的方法，可用于中高精度的simu，不仅摆脱了对转台设备的依赖，并且相比于传统方法的标定模型，考虑了加速度计标度正负不对称性系数和陀螺随机常值漂移的影响，所设计的试验操作步骤简便，参数求解过程清晰。

技术实现思路

1、本发明在考虑加速度计标度正负不对称性系数以及陀螺随机常值漂移影响的基础上，提出了一种新的标定方法，使用加速度计的静态重力模值测量直接实现加速度计标度矩阵、零偏和不对称性系数标定，采用迭代最小二乘法进行标定参数求解；再以标定好的加速度计进行水平测角作为角度参考基准，通过姿态更新解算和建立姿态解算失准角模型，完成陀螺仪标度矩阵标定；采用双位置方法标定陀螺漂移。该方法不依赖水平基准面、六面体夹具和转台等测试设备。

2、为实现上述技术效果，采用如下技术方案：

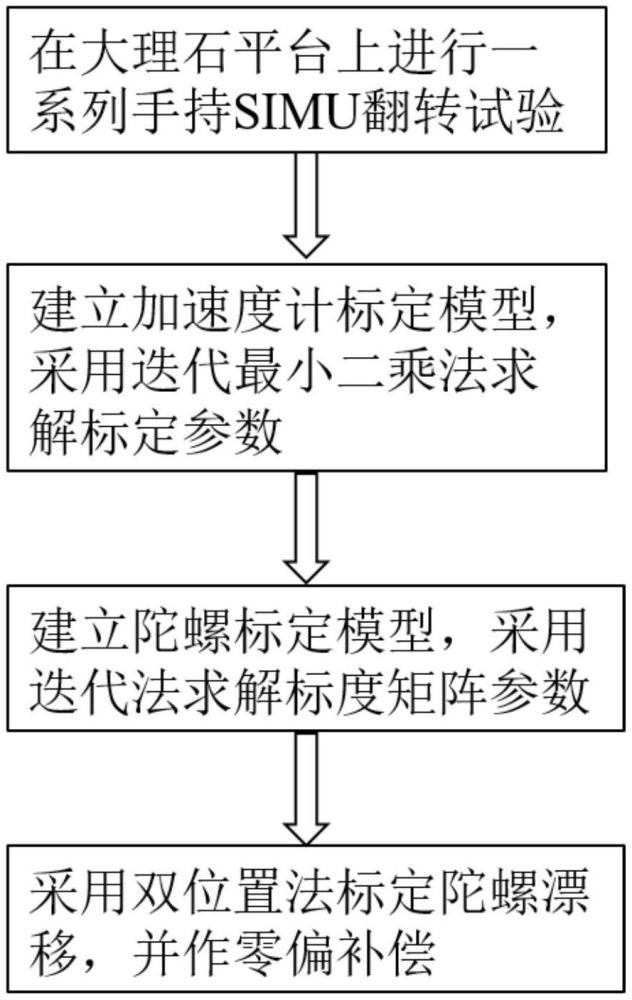
3、步骤s1：simu上电输出稳定后，在大理石平台上进行一系列“静止1-转动-静止2”的手持翻转试验；

4、步骤s2：考虑加速度计标度因数正负不对称性系数的影响，建立加速度计标定模型和标定方法，采用迭代最小二乘法求解标定参数；

5、步骤s3：在完成加速度计校准后，建立陀螺标定模型，采用迭代法求解标度矩阵参数；

6、步骤s4：采用双位置测量法标定陀螺漂移，并作零偏补偿。

7、进一步的，所述s1步骤中的手持翻转试验步骤为：

8、记地心惯性坐标系为i系，地球坐标系为e系，“东-北-天”导航参考坐标系为n系，“右-前-上”载体坐标系为b系。

9、(1)使simu的b系zb轴朝天，先置于“静止1”3min，接着绕天向zb轴旋转180°，再置于“静止2”3min；

10、(2)复用步骤(1)“静止2”后期数据30s作为本步骤“静止1”，接着绕水平xb轴旋转360°，再“静止2”30s；

11、(3)使xb轴朝天，先“静止1”30s，接着绕天向xb轴旋转180°，再“静止2”30s；

12、(4)复用步骤(3)“静止2”数据作为“静止1”，接着绕水平yb轴旋转360°，再“静止2”30s；

13、(5)使yb轴朝天，先“静止1”30s，接着绕天向yb轴旋转180°，再“静止2”30s；

14、(6)复用步骤(5)“静止2”数据作为“静止1”，接着绕水平zb轴旋转360°，再“静止2”30s；

15、(7)分别使xb轴朝地，yb轴朝地，zb轴朝地，3种放置状态各静止30s；

16、(8)分别使xbyb轴对角线朝天、地，ybzb轴对角线朝天、地，zbxb轴对角线朝天、地，6种放置状态各静止30s；

17、(9)分别使(-xb)yb轴对角线朝、地、(-xb)zb轴对角线朝天、地，(-yb)zb轴对角线朝天、地，6种放置状态各静止30s；

18、(10)分别(±xb)(±yb)(±zb)任意三轴中线朝天、地，8种放置状态各静止30s。

19、进一步的，所述s2步骤中的加速度计标定模型为：

20、记地心惯性坐标系为i系，地球坐标系为e系，“东-北-天”导航参考坐标系为n系，“右-前-上”载体坐标系为b系。

21、加速度计的标定模型为

22、

23、其中，为理想的b系比力；上标b表示载体坐标系；下标sf表示比力；为带误差的加速度计比力测量值；为加速度计偏值；kap＝［kapx kapy kapz］t为加速度计的标度因数正负不对称性系数；下标a表示加速度计；ka为加速度计标度矩阵，它可具体展开为

24、

25、其中，下标a表示加速度计；ka为加速度计标度矩阵；i表示单位矩阵；δkaij(i,j＝x,y,z)为加计标度矩阵误差δka中的元素，当i＝j时δkaii为标度因数误差，而当i≠j时δkaij为j轴加速度计对i轴的交叉耦合误差。

26、在静基座下，加速度计比力的理想模值应为当地重力加速度大小g，即有将式(2)代入式(1)，再将式(1)两边同时取模方，可得

27、

28、其中，g表示当地重力加速度大小；上标b表示载体坐标系；下标a表示加速度计；下标sf表示比力；δkaij(i,j＝x,y,z)为标度矩阵误差δka中的元素，当i＝j时δkaii为标度因数误差，而当i≠j时δkaij为j轴加速度计对i轴的交叉耦合误差；为加速度计偏值；为带误差的加速度计比力测量值；kap＝[kapx kapy kapz]t为加速度计的标度因数正负不对称性系数。

29、式(3)是关于标度误差δkaij、偏值和不对称性系数δkapi的非线性方程，考虑到它们均为小量，将式(3)展开，忽略关于小量的二阶项，可近似为如下线性方程：

30、

31、其中，g表示当地重力加速度大小；上标b表示载体坐标系；下标a表示加速度计；下标sf表示比力；δkaij(i,j＝x,y,z)为标度矩阵误差δka中的元素，当i＝j时δkaii为标度因数误差，而当i≠j时δkaij为j轴加速度计对i轴的交叉耦合误差；为加速度计偏值；为带误差的加速度计比力测量值；kap＝[kapx kapy kapz]t为加速度计的标度因数正负不对称性系数。

32、标度矩阵误差δka、偏值和不对称性系数kap为待求标定参数，共计12个独立分量。

33、将式(4)改写为关于标定参数的线性量测方程形式，为

34、ya＝haxa                            (5)

35、其中，量测ya、量测矩阵ha和待辨识参数向量xa分别为

36、

37、其中，g表示当地重力加速度大小；上标b表示载体坐标系；下标a表示加速度计；下标sf表示比力；δkaij(i,j＝x,y,z)为标度矩阵误差δka中的元素，当i＝j时δkaii为标度因数误差，而当i≠j时δkaij为j轴加速度计对i轴的交叉耦合误差；为加速度计偏值；为带误差的加速度计比力测量值；kap＝[kapx kapy kapz]t为加速度计的标度因数正负不对称性系数。

38、进一步的，所述s3步骤中的陀螺标定模型为：

39、陀螺的标定模型为

40、

41、其中，为理想的b系角速度；上标b表示载体坐标系；下标i表示惯性系；为带误差的陀螺角速度测量值；为陀螺漂移；下标g表示陀螺；kg为陀螺标度矩阵，它具体展开为

42、

43、其中，下标g表示陀螺；kg为陀螺标度矩阵；i表示单位矩阵；δkgij(i,j＝x,y,z)为标度矩阵误差δkg中的元素，当i≠j时δkgij为j轴陀螺对i轴的交叉耦合误差，包含正交旋转误差和非正交误差。

44、陀螺标度矩阵误差δkg和漂移εb为待标定参数，共计12个独立分量。

45、进一步的，所述s3步骤中的陀螺标度矩阵参数求解算法为：

46、陀螺标度误差标定是通过一系列的simu“静止1—转动—静止2”角位置和转动方案编排测试实现的，具体操作步骤如下：

47、(1)在“静止1”中，静置simu于某角位置处一小段时间，作初始对准，获得姿态阵在中会具有较高的水平姿态精度；

48、(2)在“转动”中，从“静止1”开始转动simu，以为初值，利用陀螺测量值作姿态更新解算，转动至一个新的角位置，即“静止2”角位置，记姿态阵为

49、(3)在“静止2”中，再次静置simu一小段时间，记加速度计的平均比力输出为将其转换至n系，记为

50、由计算“静止2”处陀螺姿态更新的失准角，为

51、

52、其中，φ表示失准角；g表示当地重力加速度大小；上标n表示导航坐标系；下标sf表示比力；表示导航坐标系下的加速度计平均比力输出；ez＝[0 0 1]t为天向单位矢量。

53、显然，在失准角φ＝[φe φn φu]t三个分量中，其天向失准角分量φu是无效的，仅取两个水平分量作为量测，记为

54、

55、其中，下标g表示陀螺；yg表示陀螺量测信息；φe表示东向失准角；φn表示北向失准角；g表示当地重力加速度大小；表示导航坐标系下的北向加速度计平均比力输出；表示导航坐标系下的东向加速度计平均比力输出。

56、根据捷联惯导失准角误差方程，在陀螺标定转动过程中，若只考虑陀螺标度矩阵误差，有失准角的变化规律，如下

57、

58、其中，φ表示失准角；上标n表示导航坐标系；下标b表示载体坐标系；下标i表示惯性系；表示由载体系到导航系的姿态变换矩阵；表示陀螺测量误差；下标g表示陀螺；δkg表示陀螺标度矩阵误差；表示带误差的陀螺角速度测量值；δkgi(i＝1,2,3)表示陀螺标度矩阵误差δkg的第i列向量；cg表示量测矩阵；xg表示待标定参数向量。

59、量测矩阵cg和待标定参数向量xg分别为

60、

61、

62、其中，下标g表示陀螺；上标n表示导航坐标系；下标b表示载体坐标系；下标i表示惯性系；表示带误差的陀螺角速度测量值；表示由载体系到导航系的姿态变换矩阵；δkgi(i＝1,2,3)为陀螺标度矩阵误差δkg的第i列向量。

63、将式(11)从“静止1”末了时刻(记为t1)积分至“静止2”起始时刻(记为t2)，可得失准角变化

64、

65、其中，δφ表示失准角变化量；下标g表示陀螺；cg表示陀螺量测矩阵；xg表示陀螺待标定参数向量；t1和t2分别表示试验步骤中“静止1”末了时刻和“静止2”起始时刻；hg表示由cg积分后得到的量测矩阵。

66、令式(10)与式(14)中的水平失准角分量相等，可建立关于标度矩阵误差的线性量测方程，为

67、ghg12x8                    (15)

68、其中，下标g表示陀螺；yg表示陀螺量测信息；hg1:2为由hg的第1和2行向量构造的量测矩阵；xg为陀螺待辨识的9维标定参数向量。

69、进一步的，所述s4步骤中的陀螺漂移标定模型为：

70、由双位置测量法标定陀螺漂移的公式，为

71、

72、其中，上标b表示载体坐标系；上标n表示导航坐标系；εb表示陀螺漂移；为地球自转角速度在导航坐标系的投影，ωie为地球自转角速度大小，l为当地纬度；分别为simu的zb轴朝天向时绕其旋转180°前、后的两个角位置“静止1”和“静止2”处的陀螺静态平均角速度测量值；为“静止1”处的初始对准姿态阵，而为从“静止1”姿态更新到“静止2”处的姿态阵；i表示单位矩阵；φ＝[0 0φu]t为失准角估计值；φ×表示由失准角构成的反对称矩阵。φ仅需考虑其中的方位失准分量φu，计算如下

73、

74、其中，上标b表示载体坐标系；双位置角速度差ωn表示地球自转角速度在北向的分量；ωu表示地球自转角速度在天向的分量；表示姿态阵差；l为当地纬度。