一种公路桥梁构件可靠度评定方法及系统

本发明涉及结构工程，尤其是涉及一种公路桥梁构件可靠度评定方法及系统。

背景技术：

1、在结构工程领域，公路桥梁构件的性能退化会导致桥梁可靠性随时间降低。可靠度指标作为评估桥梁性能的重要参数，可根据可靠度指标判断维修时间点。在桥梁工程中，获取可靠度指标参数非常重要。传统的桥梁时变可靠度分析方法获取结构时变可靠度，需要获取两个参数，分别是承载力的均值和方差，以及荷载效应值的均值和方差。

2、现有技术中，是通过结构材料参数统计值再代入到结构承载力计算公式当中，材料参数统计值大多是依靠实验室数值得到，其抗力的均值和方差取值，一直是一个难题。未能考虑桥梁结构实际运营状态，不是根据真实的桥梁材料参数进行评估，且桥梁状态数据不能对结构可靠度指标进行评估，进而导致时变可靠度分析方法的结果与实际有一定偏差。

技术实现思路

1、本发明的目的是提供一种公路桥梁构件可靠度评定方法及系统，通过隶属度函数结合真实的桥梁数据，获取抗弯承载力计算参数值，再获取抗弯承载力的均值和标准差，解决了公路网中预测结构时变可靠度、获取结构时变抗弯承载力的均值和标准差问题。

2、为实现上述目的，本发明提供了一种公路桥梁构件可靠度评定方法，包括以下步骤：

3、s1、获取评定构件技术状态的桥梁数据；

4、s2、利用模糊数学中的隶属度函数表示构件技术状态中的抗弯承载力计算参数的不确定性；

5、s3、利用不同构件技术状态的停留时间，通过威布尔分布的概率密度函数和生存函数求解半马尔可夫概率转移矩阵，获得随时间变化的构件技术状态的概率分布；

6、s4、基于抗弯承载力计算公式，输入构件截面设计参数值，利用隶属度函数与半马尔可夫过程结合获得抗弯承载力计算参数的变量参数随时间变化的结果值，再通过蒙特卡洛模拟求解多次构件抗弯承载力，并对构件抗弯承载力进行统计，获得其均值和标准差；

7、s5、基于极限状态方程，输入荷载效应值的均值和标准差，输入s4得到的抗弯承载力均值和标准差，利用蒙特卡洛模拟获取构件时变可靠指标。

8、优选的，所述构件技术状态包括 i个状态等级， i=1、2、3...n，n为整数，其中，第1状态等级表示桥梁处于功能完好的全新状态。

9、优选的，根据第 i状态等级的停留时间划分退化速率等级，退化速率等级包括极慢速、慢速、中速、快速和极快速。

10、优选的，s2中，利用模糊数学中的隶属度函数表示构件技术状态中的抗弯承载力计算参数的不确定性，具体为：

11、抗弯承载力计算公式：

12、；

13、其中，为混凝土抗压强度，为钢筋抗拉强度，为抗拉钢筋截面面积，为构件宽度，为构件有效高度；

14、所述抗弯承载力计算参数包括、和，、和均为构件随时间变化的变量参数，和为构件的非变量参数；

15、根据抗弯承载力计算参数的材料损伤区间，获取随第 i状态等级变化的模糊程度区间，进而得到构件抗弯承载力的时变值。

16、优选的，s3具体如下：

17、马尔可夫链的性质表示为：

18、；

19、其中，p为条件概率，为 t时刻对应的第 i状态等级；

20、在马尔可夫链中，其转移过程的单步转移概率指给定时间段从第 i状态等级转移到第 j状态等级的概率，表示为：

21、,where；

22、其中，m为退化过程中第 i状态等级/第 j状态等级的数量；

23、马尔可夫过程和半马尔可夫过程的区别在于状态转移机制的时间依赖性，则半马尔可夫概率转移矩阵p’为：

24、and；

25、则 t时刻的第 i状态等级概率为：

26、；

27、其中，是在时间为 t年的半马尔可夫概率转移矩阵，为 t-1年的每个状态等级概率分布；

28、第 i状态等级随时间 t的概率密度函数和生存函数分别表示为：

29、

30、；

31、其中，和分别为在第 i状态等级时威布尔分布的尺度参数和形状参数，为的原函数；

32、通过威布尔分布的生存函数和概率密度函数计算得到，每个时间节点 t、两个相邻状态等级之间的状态转移概率，表示为：

33、；

34、其中，是累积停留时间的概率密度函数，和分别是停留时间和的生存函数，取值为1年；

35、同时，第 i状态等级随时间 t的威布尔分布生存函数接近于构件所在等级，随时间 t保持相同第 i状态等级的概率，两者差值表示为：

36、；

37、通过求解最小化问题，计算出任意第 i状态等级下威布尔分布中的尺度参数和形状参数，表示为：

38、；

39、其中，是在时刻保持相同第 i状态等级的概率，为第 i状态等级的停留时间。

40、优选的，s4中，将加入到构件抗弯承载力计算公式中，则：

41、；

42、则混凝土强度、钢筋抗拉强度、钢筋截面的损失量分别表示为：

43、

44、

45、；

46、其中，为 t时刻第 i状态等级概率，为第 i状态等级钢筋截面损失率，为第 i状态等级钢筋抗拉强度损失率，为第 i状态等级混凝土强度损失值。

47、优选的，s5中，极限状态方程为：

48、；

49、其中，为结构可靠性函数，为抗弯承载力，为荷载效应值。

50、优选的，时变可靠指标表示为：

51、；

52、其中，为 t时刻构件可靠指标，、分别为 t时刻构件时变抗弯承载力均值、标准差；、分别为构件时变荷载效应值的均值、标准差。

53、为实现上述目的，本发明还提供了一种公路桥梁构件可靠度评定系统，包括：

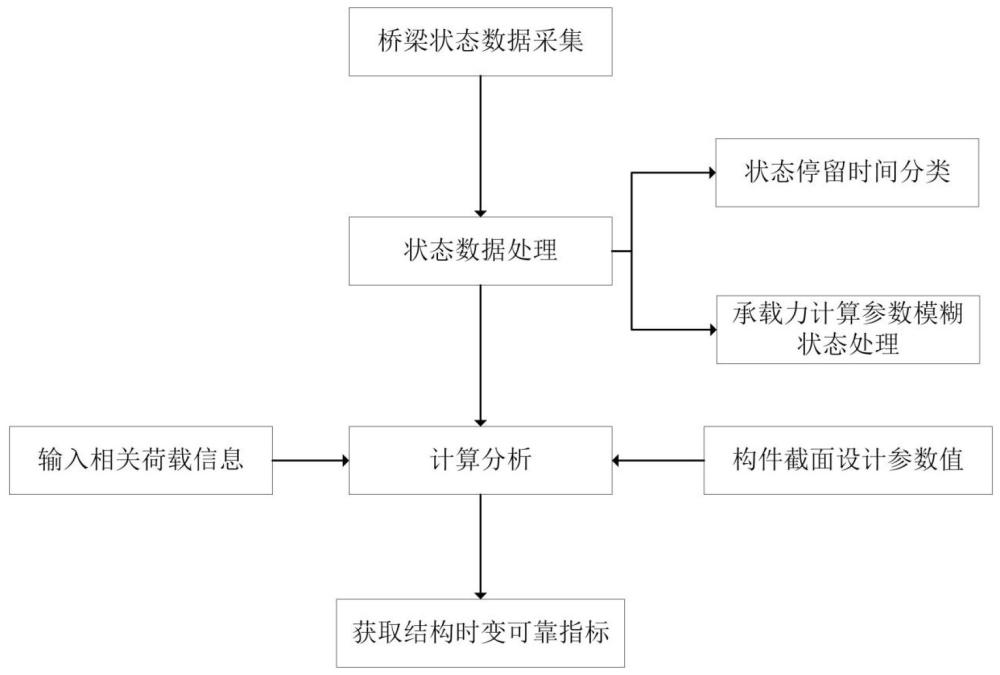
54、桥梁状态数据储存模块，用于储存或更新实际采集的桥梁状态数据；

55、状态数据处理模块，用于第 i状态等级下的停留时间分类以及退化速率下的概率分布，对抗弯承载力计算参数进行模糊状态处理；

56、计算分析模块，用于以荷载信息和构件截面设计参数值作为输入数据，获取时变可靠指标作为输出数据，模拟构件时变可靠度。

57、因此，本发明采用上述一种公路桥梁构件可靠度评定方法及系统，有益效果如下：

58、（1）本发明通过隶属度函数结合真实的桥梁数据，获取抗弯承载力材料参数值，再获取时变抗弯承载力的均值和标准差，解决了公路网中预测结构时变可靠度、获取结构时变抗弯承载力的均值和标准差问题。

59、（2）本发明根据构件的第 i状态等级的停留时间判断构件的退化速率等级，输入构件抗弯承载力初始计算参数，可获得构件时变抗弯承载力的均值与标准差，利用获得的抗弯承载力值，求解构件时变可靠指标，保证可靠度分析符合实际退化过程；同时，输入相关荷载信息对桥梁性能进行判断。

60、下面通过附图和实施例，对本发明的技术方案做进一步的详细描述。