一种深度神经网络拓扑结构约束学习方法

本发明属于人工智能和神经生物学领域，具体涉及到一种深度神经网络拓扑结构约束学习方法。

背景技术：

1、深度神经网络研究中的一些关键概念可以追溯到大脑的研究，其研究经常从神经科学领域获得灵感。目前，这些灵感主要集中在网络的功能结构，视觉表征的相似性，或者网络训练过程的生物合理性等方面。也有一些研究以生物网络拓扑为启发，但主要集中在神经网络拓扑与生物脑网络拓扑的抽象相似性上。例如，使用与生物脑网络具有抽象相似性的拓扑结构构建神经网络，而不是手工设计构建人工神经网络，如watts-strogatz模型或barabási-albert模型。

2、虽然这些方法利用了生物大脑的网络拓扑，但它们只是在抽象的层面上，并没有纳入生物大脑网络拓扑的真实神经数据。大脑具有典型的全局网络，包括模块化和短路径长度，这反映了大脑不同区域的神经元群体如何相互连接。计算神经科学也证实了大脑网络是认知的基础，生物大脑高度结构化的网络拓扑结构是重要的先验知识，这些先验知识也许能够用于提升神经网络的工程性能。然而，目前缺乏将神经生理学记录直接转化为人工神经网络改进的技术。因此，如何将真正的生物大脑拓扑数据整合到人工神经网络中，并提升人工神经网络的性能，仍然是一个亟待解决的问题。

技术实现思路

1、针对上述存在的问题或不足，本发明提供了一种深度神经网络拓扑结构约束学习方法，旨在解决目前缺乏将神经生理学记录直接整合到人工神经网络中的技术，以提升人工神经网络的性能。

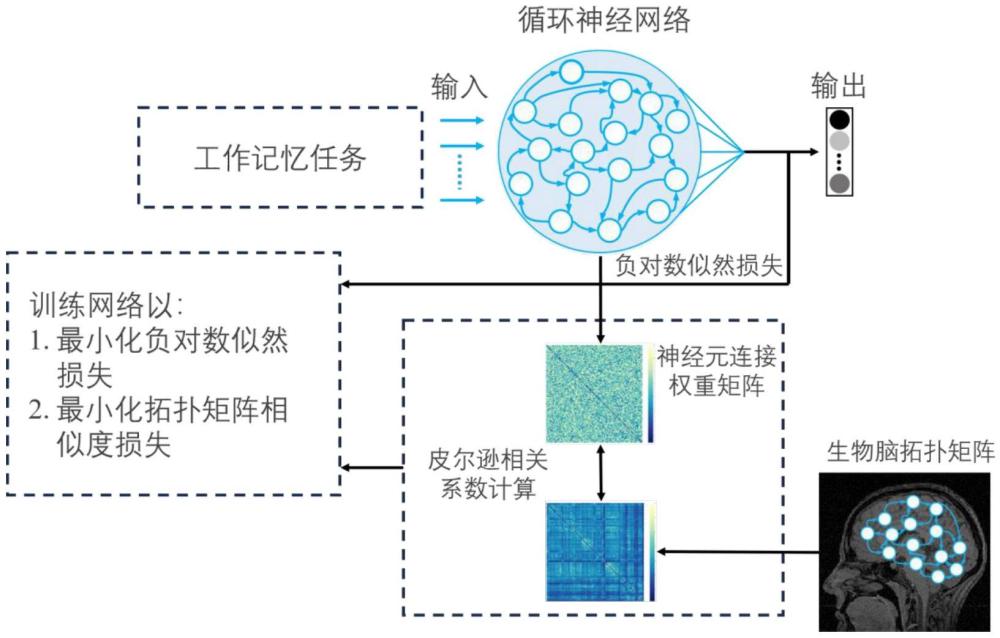
2、一种深度神经网络拓扑结构约束学习方法，具体步骤如下：

3、步骤1、获取生物脑拓扑矩阵数据并搭建深度神经网络模型。

4、对获取的静息态功能磁共振数据进行预处理。

5、基于脑分区模板将预处理后的数据划分为m个脑区，m的取值范围为[2,116]，通过计算不同脑区之间的皮尔逊相关系数得到生物脑拓扑矩阵bm×m。其中矩阵bm×m中第i行第j列元素(即第i个脑区与第j个脑区的皮尔逊相关系数)的计算式为：

6、

7、式中ti和tj分别为第i脑区与第j脑区的时间序列，与分别为第i脑区与第j脑区时间序列的平均值。

8、采用rnns循环神经网络作为深度神经网络的模型，由输入层、隐藏层和输出层组成。其隐藏层的状态方程为：

9、ct＝wihxt+bih+whhrt-1+bhh，rt＝fh(ct)

10、输出层的输出方程为：

11、yt＝fy(wyrt+by)

12、其中ct为神经元在时间t的状态变量，wih、whh和wy分别是输入层、隐藏层以及输出层的神经元连接权值矩，xt是rnns在时间t的输入，rt是隐藏层在时间t的神经活动，bih、bhh和by分别是输入层、隐藏层以及输出层的的偏置项，yt是rnns在时间t的输出，fh(·)和fy(·)分别是隐藏层和输出层的激活函数。

13、进一步的，所述rnns循环神经网络：输入层神经元数量为2，第一个神经元n1用于接收任务的一维向量，第二个神经元n2用于接收状态指令；当n2接收0时表示模型处于认知任务的刺激展示阶段，接收1时表示模型处于认知任务的反应阶段。隐藏层神经元数量与脑区数量相同，为m个。输出层神经元数量为3，输出3种标签，定义为1、0、-1；1表示在认知任务反应阶段输出为匹配，-1表示在认知任务反应阶段输出为不匹配，0表示认知任务刺激展示阶段(非反应阶段)的输出标签。

14、步骤2、使用生物脑拓扑结构约束神经网络的学习过程进而训练模型。

15、将生物实验中采用的认知任务实验范式用于训练步骤1搭建的深度神经网络，以执行生命科学领域的工作记忆任务。训练时，深度神经网络的输入依次为：

16、随机生成数a输入到输入神经元n1，同时将0输入到神经元n2，此阶段为刺激展示阶段；

17、接着，随机生成数b输入到输入神经元n1，同时将0输入到神经元n2，此阶段为刺激展示阶段；

18、接着，随机生成数c输入到输入神经元n1，同时将1输入到神经元n2，此阶段为反应阶段；

19、上述输入流程中，相对应的模型正确输出为：若随机生成数c和随机生成数a相同，则模型反应阶段应该输出标签1，表示匹配；若随机生成数c和随机生成数a不相同，则模型反应阶段应该输出标签-1，表示不匹配；在刺激展示阶段，模型应该输出标签0。

20、随机生成d次上述随机生成数a、b、c，组成d个上述认知任务作为训练集用于训练神经网络。

21、同时，随机生成e次上述随机生成数a、b、c，组成e个上述认知任务作为测试集用于测试训练完成的神经网络的性能。

22、在使用d个上述认知任务作为训练集来训练神经网络时，使用反向传播算法更新神经网络参数，反向传播算法的损失函数同时包含负对数似然损失costtask与拓扑矩阵相似度损失costsimilarity，具体定义为：

23、cost＝costtask+αcostsimilarity

24、costtask＝logp(yi|xi)

25、

26、其中，α为可调参数；p(yi|xi)表示神经网络输入为xi时，输出为正确输出yi的概率；为bm×m矩阵的均值，为whh矩阵的均值。

27、训练时，批大小为batch≥32，迭代次数为epoch≥100。迭代次数达到epoch后，则训练完成，分别将e个上述作为测试集的认知任务的输入数据输入到神经网络的输入层中，统计对应的神经网络实际输出等于正确输出的次数为corrt，则正确率为corrt/e；同时计算训练完成后的costsimilarity，作为神经网络与生物脑在拓扑结构上的相似性。上述两指标作为神经网络最终的性能参数。

28、进一步的，所述步骤1的预处理方法以及目的依次是：去时间点(避免初始化时间阶段的影响)、时间层矫正(提高信号的时间一致性)、头动矫正(减少由于头动引起的伪影)、空间标准化(转换到标准空间便于不同个体数据的比较)、平滑(减少信号噪声提高信噪比)、去线性漂移(减少伪信号的影响)和滤波(去除噪声和不相关的频率成分)。

29、进一步的，所述步骤2中反向传播算法采用梯度下降算法对循环层(神经网络参数)进行迭代更新，梯度下降算法的公式为：

30、

31、其中θk表示第k次迭代时神经网络的参数集合，cost(θk)表示损失函数cost针对θk的具体表示，ir表示网络学习率。

32、进一步的，网络学习率控制着每次迭代更新参数的幅度，过高或过低的学习率都会降低模型的训练效果。本发明在迭代训练过程中，对学习率进行衰减，以此提高网络训练效率，所述网络学习率ir衰减公式为：

33、

34、综上所述，本发明通过神经网络训练的目标是最小化损失函数，在损失函数中加入了衡量神经网络拓扑矩阵与生物拓扑矩阵(神经生理学记录)相似度的指标，以最小化负对数似然损失和最小化拓扑矩阵相似度损失，因此模型训练后会使神经网络的拓扑矩阵偏向于生物拓扑矩阵，从而实现将神经生理学记录直接整合到人工神经网络的技术，填补了将神经生理学记录直接转化为人工神经网络改进的技术空白，从而提升神经网络的工程性能。