基于代理模型预测的跨介质飞行器击水弹跳轨迹生成方法

本发明涉及一种基于代理模型预测的跨介质飞行器击水弹跳轨迹生成方法，属于飞行器轨迹规划。

背景技术：

1、跨介质飞行器是一种兼具海空两栖作业能力的特种飞行器，不仅兼具航空器和水下航行器的特点，还可以突破水域和空域的介质隔离，提高跨水空任务成功的可靠性，具有巨大的应用潜力。跨介质飞行器轨迹规划是实现其自主飞行关键技术之一。近水面滑跳作为跨介质飞行器的一种特殊飞行方式，相比高空投射有着更好的机动性和精准性，可以有效提升飞行器的飞行航程和自身生存能力。

2、跨介质飞行器任务轨迹生成需要考虑不同飞行阶段的特点进行设计。整个飞行阶段可分为空中飞行段和击水段。空中飞行段的轨迹生成需要考虑跨介质飞行器的飞行性能、状态边界等约束，以时间最短或飞行航程最短等为性能指标，为飞行器生成一条可行的最优轨迹。对于击水段，现有的跨介质飞行器击水弹跳轨迹生成方法主要是将流体和飞行器之间的作用力加以考虑，对跨介质飞行器进行精确动力学建模，求解得到相应结果，或将飞行器抽象为平板或圆柱体进行动力学建模。但是由于击水过程包含了空气、水和飞行器之间的相互作用过程，使得跨介质飞行器的运动具有随机性和未知性，相关作用力难以得到显示表达式。同时，跨介质飞行器种类较多，形态各有所异，其仿真模型计算难度大、耗费时间长。因此，有必要开展跨介质飞行器与代理模型的融合研究，可在满足可靠性的前提下降低模型研究成本。

3、针对上述问题，本发明提出一种基于代理模型的跨介质飞行器击水弹跳轨迹生成方法，用于规划跨介质飞行器全过程的击水飞行轨迹。通过仿真采集不同工况下跨介质飞行器击水前后的状态量样本构造代理模型，对击水段前后状态量进行非线性映射，进而对真实情况下的击水后状态进行预测，解决了跨介质飞行器击水段精确动力学模型推导难和简化建模精度低的问题，为跨介质飞行器多阶段飞行任务的完成提供可靠技术支撑。

技术实现思路

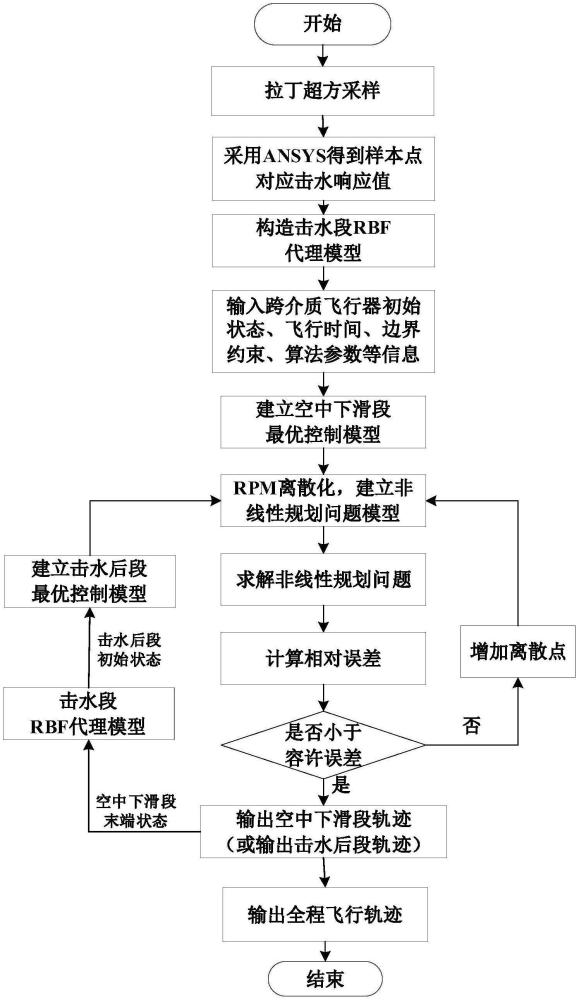
1、为解决跨介质飞行器击水段精确动力学模型推导难和简化建模精度低的问题，本发明提供一种基于代理模型预测的跨介质飞行器击水弹跳轨迹生成方法，该方法通过对击水段不同工况进行仿真采样，构建代理模型对击水前后的状态量进行非线性映射，其次将跨介质飞行器飞行轨迹生成问题建模为最优控制问题；利用伪谱法对非线性最优控制问题进行迭代求解，直至满足所有轨迹约束，生成跨介质飞行器击水全过程的飞行轨迹。本发明能够对飞行器击水后状态进行预测，避免真实飞行器仿真模型导致计算难度大、耗费时间长的问题，具有精度高和可靠性高的优点。

2、本发明的目的是通过下述技术方案实现的。

3、基于代理模型预测的跨介质飞行器击水弹跳轨迹生成方法，其特征在于：包括如下步骤：

4、步骤一：生成一组拉丁超方采样点集，四个维度分别为速度倾角θsample、速度vsample、攻角αsample与质量msample，并通过有限元软件仿真得到拉丁超方采样点集对应的响应值，即跨介质飞行器击水前后的位置[xres,yres]、速度vres、俯仰角攻角αres；将若干组响应值构建成样本点数据库；

5、步骤二：利用步骤一的样本点数据库构造径向基函数rbf代理模型；

6、

7、式中，

8、

9、其中，z为输入值，ns为构造径向基函数代理模型的样本规模，为权重系数，由式(2)—式(3)计算得到。φ为径向函数；ci表示步骤一中构建的样本点集，w表示步骤一中样本点的响应值；代理模型的输出值，即为跨介质飞行器击水后的飞行状态；

10、步骤三：设置跨介质飞行器的初始仿真参数；所述初始仿真参数包括：跨介质飞行器推力p(t)、各阶段飞行时间ti(i＝phase1,phase2,phase3)、初始位置[x0,y0]、初始速度v0、初始质量m0、初始弹道倾角θ0、初始攻角α0、状态边界smin,smax、控制边界umin,umax以及最大容许误差εd；

11、步骤四：基于性能指标、动力学约束、状态约束和控制量约束，建立跨介质飞行器空中滑翔段和低空飞行段的最优控制模型；

12、跨介质飞行器轨迹生成的性能指标j为飞行航程最大：

13、j＝-x (4)

14、x为跨介质飞行器的水平位置；

15、跨介质飞行器的动力学约束表示为：

16、

17、其中，s＝[v,θ,x,y,m,α]为跨介质飞行器的状态量，v为速度、θ为弹道倾角、x为水平位置、y为竖直位置、m为质量、α为攻角；p表示飞行器推力、x表示气动阻力、y表示气动升力，mc表示质量流率，为攻角变化率；g为重力加速度；

18、跨介质飞行器高空飞行段、低空飞行段和击水后段的状态约束包括：初始状态约束如式(6)、终端状态约束如式(7)和状态边界约束如式(8)；

19、

20、θ(tf)＝θf, y(tf)＝yf (7)

21、

22、其中，t0表示初始时刻，tf表示终端时间，v(t)表示v在t时刻的值，其余变量以此类推；s0＝[v0,θ0,x0,y0,m0,α0]表示各阶段初始状态，[θf,yf]表示各阶段状态量终端状态，smin＝[vmin,θmin,xmin,ymin,mmin,αmin]和smax＝[vmax,θmax,xmax,ymax,mmax,αmax]分别表示各阶段状态的下边界和上边界；

23、考虑执行机构的能力，避免控制系统因控制量高频变化而出现失稳现象，需要限制控制量的变化范围，即

24、

25、其中，控制量为攻角变化率，表示攻角变化率最小值，表示攻角变化率最大值；分别表示各阶段控制量的上边界和下边界；

26、根据式(4)～(9)建立针对跨介质飞行器空中段轨迹生成最优控制问题模型

27、

28、其中，u为控制量，即为第i段的攻角变化率；xi为第i段的飞行器水平位置；phase1表示高空飞行段、phase2表示低空飞行段、phase3表示击水后段，均为跨介质飞行器空中飞行段；该问题需要使每一段满足约束的条件下，寻找一组控制量使得性能指标最小；

29、步骤五：将步骤四中建立的最优控制问题经过离散化和数值近似，转化为非线性规划问题；

30、步骤5.1：离散化过程如下：

31、将区间[t0,tf]均匀划分为k个网格子区间，每个网格子区间的时间步长为△t＝(tf-t0)/k，然后将每个网格子区间[tk-1,tk]上的状态量和控制量在离散点上进行离散，并通过构造插值多项式进行逼近，从而将微分方程转化为代数方程约束；

32、将每个网格子区间的时域t∈[tk-1,tk]通过式(11)变换到变量τ∈[-1,1]；

33、

34、设第k个网格子区间的状态量和控制量分别为s(k)(τ)和u(k)(τ)，为保证各网格子区间之间状态的连续性，增加式(12)所示的内网点约束条件，即

35、s(k)(+1)＝s(k+1)(-1), k＝0,1,...,k-1 (12)

36、通过式(11)和(12)的变换，将最优控制问题转化为多区间最优控制问题，式(4)所示的性能指标转化为最小化多区间bolza型代价函数：

37、

38、其中，φ表示mayer型代价函数，g表示lagrange型代价函数。

39、综上，经式(11)～式(13)的变换，考虑增加内网点约束的多区间bolza型性能指标的最优控制问题表示如下：

40、

41、其中，f和分别为动力学约束和状态量始末约束；

42、步骤5.2：利用数值近似对跨介质飞行器的动力学方程、边界条件和过程约束进行近似，转化成伪谱法的一般求解形式，从而将步骤5.1建立的转化为非线性规划问题；

43、设s(k)(τ)和u(k)(τ)分别表示第k个子区间[tk-1,tk]内的状态量和控制量；

44、取nk阶lgr点和末点作为节点，在区间τ∈[-1,1]内采用nk+1个lagrange插值多项式对状态量s(k)(τ)和控制量u(k)(τ)进行近似：

45、

46、其中，s(k)(τ)和u(k)(τ)分别为近似后的状态量和控制量，si(k)表示状态量在区间[tk-1,tk]内第i个配点的值，ui(k)表示控制量在区间[tk-1,tk]内第i个配点的值；li(τ)i＝1,...,nk+1为nk阶lagrange插值多项式，即：

47、

48、式中，τi和τj表示radau伪谱法在区间[tk-1,tk]内的任意两个不重复的配点。

49、对式(15)求微分，得

50、

51、则lgr点上的动力学微分方程约束转化为代数方程约束：

52、

53、式中，为第k个子区间的伪谱微分矩阵。

54、每个网格子区间内nk个配点上的边界约束为：

55、

56、网点上的状态约束为：

57、

58、将多区间bolza型性能指标(13)中的积分项用多区间gauss积分近似，得到

59、

60、式中，为第k个子区间内的lagrange型代价函数；为第k个子区间内的legendre-gauss-radau权重，表示为：

61、

62、经式(15)～(22)的数值近似过程，最终将转变为带有约束条件的非线性规划问题

63、

64、步骤六：利用伪谱法对进行求解，获得的求解结果，即跨介质飞行器高空飞行段和低空飞行段的飞行轨迹；

65、步骤七：根据式(25)进行判断，若步骤六结果满足式(25)，则输出的求解结果，执行步骤八；若不满足，则通过式(26)增加离散点，并转步骤五；

66、

67、其中，为第k个子区间[tk-1,tk]内选取的第s个采样点，ceil(·)为向上取整函数，nd为正整数，用来调节新增的离散节点个数；表示为第k个子区间内的最大误差；

68、步骤八：输出的求解结果，得到高空飞行段和低空飞行段的飞行轨迹，并通过步骤二构建的代理模型获得跨介质飞行器击水后的飞行状态；

69、以求解结果的轨迹末状态中的速度倾角θf、速度vf、攻角αf、质量mf作为自变量输入到代理模型(1)中，得到击水后的跨介质飞行器初始状态，即：

70、xinput＝[θf,vf,αf,mf] (27)

71、

72、其中，xinput表示求解的轨迹末状态，xoutput表示求解得到的击水后的飞行器状态量，同时也表示为击水后段的初始状态x0,phase3；

73、步骤九：基于步骤八得到的击水后段初始状态x0,phase3，建立击水后段最优控制模型，转步骤五进行求解，获得击水后段飞行轨迹；

74、步骤十：输出并拼接步骤六得到的高空飞行段轨迹、低空飞行段的轨迹和步骤九得到的击水后段飞行轨迹，得到所有轨迹，即为基于代理模型预测的跨介质飞行器击水弹跳轨迹生成结果；

75、还包括步骤十一：根据步骤十得到的飞行器击水弹跳轨迹生成结果，可以得到跨介质飞行器多任务阶段的全部飞行轨迹，使跨介质飞行器在满足各阶段约束的前提下从给定位置经过一次或多次击水弹跳到达目标位置范围，实现高精度低计算量的跨介质飞行器击水飞行。

76、有益效果：

77、1、本发明公开的基于代理模型预测的跨介质飞行器击水弹跳轨迹生成方法，将跨介质飞行器轨迹生成问题建模为带有约束条件的非线性规划问题，并基于伪谱法进行求解，获得满足约束的可行空中段飞行轨迹，提高跨介质飞行器轨迹生成的可靠性。

78、2、本发明公开的基于代理模型预测的跨介质飞行器击水弹跳轨迹生成方法，使用拉丁超方设计作为采样方法，能够通过有限迭代次数的抽样比较准确地重建输入分布，为代理模型的构建提供空间覆盖率更高的样本，减少跨介质飞行器使用简化模型导致的建模误差，对击水段后的飞行器状态量预测结果有较高的准确性。

79、3、本发明公开的基于代理模型预测的跨介质飞行器击水弹跳轨迹生成方法，通过有限元软件仿真构建的代理模型对击水段前后状态量进行非线性映射，不需要推导精确的击水段动力学方程，显著降低建模导致的计算复杂性，提高跨介质飞行器击水弹跳轨迹生成的效率。