一种四轮无人自主小车的轨迹跟踪控制方法

本发明属于无人驾驶汽车轨迹跟踪控制，具体涉及一种四轮无人自主小车的轨迹跟踪控制方法。

背景技术：

1、近几年来，随着无人驾驶技术的快速发展和广泛应用，有关无人驾驶的关键技术吸引了大量国内外学者的青睐和研究。一方面，对无人驾驶技术的研究为现代智能汽车的开发提供了理论基础，另一方面，日益成熟的无人驾驶技术能大大提升车辆乘坐舒适性和汽车行驶安全性，同时为智能交通系统的发展和应用提供技术支撑。

2、pid控制算法就在汽车工业界广泛使用，但是由于无人驾驶汽车行驶过程的内部参数(速度，横摆角，转向角)和外部参数(道路曲率，风阻系数)一直在变化，因此调节参数的过程就会非常复杂，适应性就会很差，很难在实际的无人驾驶车辆中广泛的使用。再比如说一些新兴的算法，诸如强化学习算法，自适应神经网络算法，大多数都是通过预设好道路的条件或者提前获得训练数据集来进行无人驾驶车辆的轨迹研究，根本就无法满足无人驾驶车辆的实施控制需求。

技术实现思路

1、为克服上述现有技术的不足，本发明的目的是提供一种四轮无人自主小车的轨迹跟踪控制方法，可有效提升无人驾驶车辆的轨迹跟踪性能。

2、为实现上述目的，本发明采用的技术方案是：一种四轮无人自主小车的轨迹跟踪控制方法，包括以下步骤：

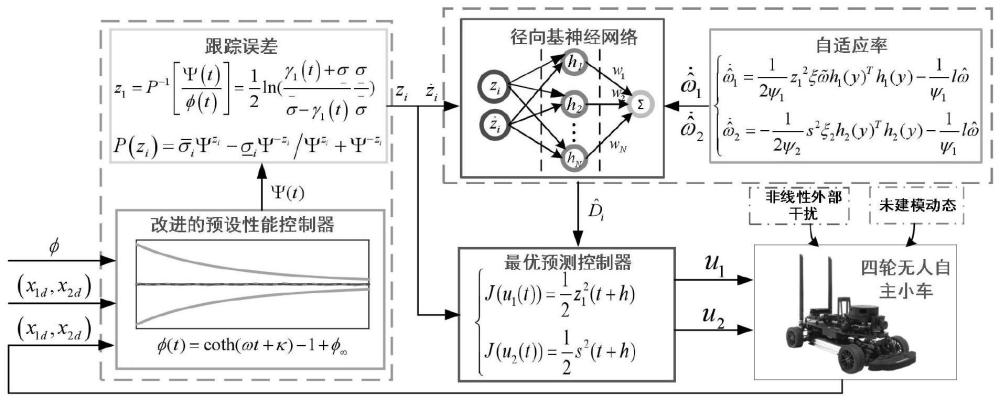
3、步骤1，建立四轮无人自主小车的二自由度动力学模型；

4、步骤2，构建具有预设预测性能的轨迹跟踪控制器，在轨迹跟踪控制器的预设模型中加入新型性能函数；

5、步骤3，设计轨迹跟踪控制器的约束方程，构件轨迹跟踪控制器的控制轨迹输入；

6、步骤4，结合神经网络，求解下一个时刻控制系统的输入。

7、所述的步骤1中四轮无人自主小车的二自由度运动学模型为无人驾驶车辆的运动学状态空间方程，步骤1具体过程为：

8、根据无人驾驶车辆的运动学关系，基于牛顿第二定律可得：

9、

10、式(1)中，f4＝mgsinαx sinθk，m为四轮无人自主小车的重量，f1车轮的驱动力，f2车轮的摩擦力，f3车轮的制动力，f4为重力的分力，vk为小车的速度，k为驱动增益系数，ul为小车左轮输入力矩，ur为小车左轮输入力矩，c为粘性摩擦系数，r为车轮半径，iw为小车转动惯量，g是重力系数，θk为小车的转向角度，αx为小车的转向加速度，

11、注：公式中参数上一点为该字母的一阶导数，两个点为该字母的二阶导数，例如为vk的一阶导数，为的二阶导数，

12、则式(1)改写为：

13、

14、此外，根据力矩平衡原理得：

15、m1＝m2-m3-m4      (3)

16、式(3)中，m1、m2、m3和m4分别为驱动力、矩摩擦力矩、制动力矩、和重力的分力力矩，

17、同理得：

18、

19、式(4)中，l为小车质心到车轮中线的垂直距离，ωk为小车角速度，结合(2)和(4)得：

20、

21、式(5)中，和为中间变量，

22、为便于具有预设预测性能的控制器设计，选择u1和u2作为fwmr的中间控制变量，表示为:

23、u1＝ul+ur,u2＝ul-ur         (6)

24、在实际应用中，fwmr系统不可避免地存在非线性外部扰动和未建模的动力学，这些扰动会导致系统不稳定和性能损失:对于fwmr，需要考虑fwmr可能存在的非线性扰动，用di表示，i＝1,2，定义x1＝vk，x2＝θk，x3＝ωk，则：

25、

26、其中，fn(x1)＝g1x1,gn(x1)＝b1,fn(x2)＝g2和gn(x2)＝b2是中间变量。

27、所述的步骤2，具体做法是：

28、构建跟踪误差：

29、[x1-x1d,x2-x2d]t＝[ψ,θ]t                    (8)

30、式(8)中，x1d为理想速度轨迹，x2d为理想角度轨迹，ψ和θ为中间变量，

31、为消除对精确初始误差的要求，选择构建新型的性能函数为：

32、φ(t)＝coth(ωt+κ)-1+φ∞                     (9)

33、式(9)中，ω和κ为正调节参数，φ∞为系统在稳定状态下的允许误差，保持性能约束始终满足，误差变换如下：

34、

35、其中，z1和z2是转换误差，ψ(t)和θ(t)为中间变量，p(zi)为转换函数，i＝1,2，p(zi)可被选择为：

36、

37、式(11)中，和σ为正常数，

38、由于φ(t)≠0，根据(17)得：

39、

40、其中，是中间变量，

41、求导得：

42、

43、式(13)中，为中间变量，

44、z2的二阶导得：

45、

46、定义滤波误差：

47、

48、得：

49、

50、式(16)中，λ＞0。

51、所述的步骤3，预设预测控制器的约束方程具体过程为：

52、构造包含u1和u2的opc控制器的目标是使代价函数最小，所以选择opc的代价函数为：

53、

54、式(17)中，h为预测步长，t为时间，u1(t)为系统一的输入，u2(t)为系统二的输入，

55、式(17)泰勒展开为：

56、

57、式(18)中，p为展开阶数，

58、对于所控制的四轮无人自主小车，展开阶数选择为1：

59、

60、结合模型公式得：

61、

62、最终得到系统得控制输入得：

63、

64、步骤4具体过程为：

65、为了减轻外部干扰和未建模动态对四轮无人自主小车得影响，使用改进得径向基神经网络来补偿(7)中的d:

66、径向基神经网络表示为：

67、di＝withi(y)+οi(i＝1,2,3)      (22)

68、式(22)中，wi＝[wi1 …,win]t为神经网络的权重，oi为逼近误差的估计值，i＝1,2,3…n，是高斯基函数,j＝1,2,…,n，高斯基函数中j为第j个隐藏层，cj和τj为高斯函数的最有中心和最优宽度，y为网络的输入信号，

69、采用最小参数估计法简化了神经网络逼近过程，提高了自适应算法的收敛速度，定义ωx＝||wx||2，则近似误差可表示为

70、逼近系统外部干扰后的控制率可以表示为：

71、

72、其中自适应率和为：

73、

74、式(24)中，ψ1、l和ψ2∈r+为中间变量。

75、本发明的有益效果是：

76、本发明针对四轮无人小车的轨迹跟踪控制，使用了一种结合预设性能控制和最优预测控制相结合的轨迹跟踪控制器，由于该控制器可以有效的约束跟踪误差并且产生连续的控制信号，相较于pid算法和滑模算法，其控制精度更高，控制效果更加平稳，且可以保证追踪误差始终保持在误差约束范围内；本发明的控制方法能够有效提高四轮无人小车的行驶稳定性和安全性，对其精确的轨迹跟踪控制具有重大意义。