一种变拓扑自驱动自适应时域快速模型预测控制方法与流程

本发明涉及属于自动控制，具体地，涉及一种变拓扑自驱动自适应时域快速模型预测控制方法。

背景技术：

1、随着太空任务的不断深入和航天技术的迅速发展，轻量化、模块化的大型空间结构具有广泛的应用需求基础。受限于运载火箭的单次运载能力，在轨组装是大型空间结构最有前景的构建方式之一。随着空间机器人技术的不断发展，在轨组装技术在未来大型甚至超大型空间结构的构建中将发挥更大的潜力。在轨组装过程是一个时变的动力学行为，随着空间结构的不断“生长”，其几何尺寸和惯量参数发生阶跃式增加。较大质心变化引起的系统相对阶的结构、控制方向、系统耦合性等的变化以及碰撞过程的非光滑因素，会造成系统性能急剧下降，甚至失稳。同时，考虑到高精度观测等任务，对大型组装结构的姿态稳态精度和稳定时间提出了更高的要求，而复杂的环境干扰、柔性振动耦合、平台与局部载荷子系统之间的强动力学耦合等因素都对指向精度和稳定度产生较大影响。因此，亟需发展包含变拓扑多约束鲁棒稳定控制算法，实现支持在轨组装平台的高精高稳控制。

2、目前，关于变拓扑自驱动自适应时域快速模型预测控制方法主要集中以下几个方面：(1)基于预置性能的多约束控制，(2)基于自适应控制的在线迭代控制；(3)基于反步法技术的在轨组装鲁棒控制技术等。在以往的在轨组装控制设计过程中，通常情况下面对复杂约束下的在轨组装过程控制，通常多约束条件是依赖人工经验将部分约束引入到控制器设计中，难以满足在轨组装复杂的多约束要求。上述的研究均解决部分约束或者同类约束下的在轨组装稳定控制问题，无法实现以最优的方式同时兼顾多种在轨组装约束。

技术实现思路

1、为了克服现有技术中存在的不足，本发明针对在轨组装不断生长的时变动力学模型，提供了一种变拓扑自驱动自适应时域快速模型预测控制方法，该方法基于自驱动技术和时变预测步长的快速模型预测控制技术，保证在轨组装系统能够应对时变的组装过程，保障其安全性，提高了时变在轨组装过程的控制性能。

2、为了实现以上目的，本发明是通过以下技术方案实现的：

3、一种变拓扑自驱动自适应时域快速模型预测控制方法，其特点是，包括如下步骤：

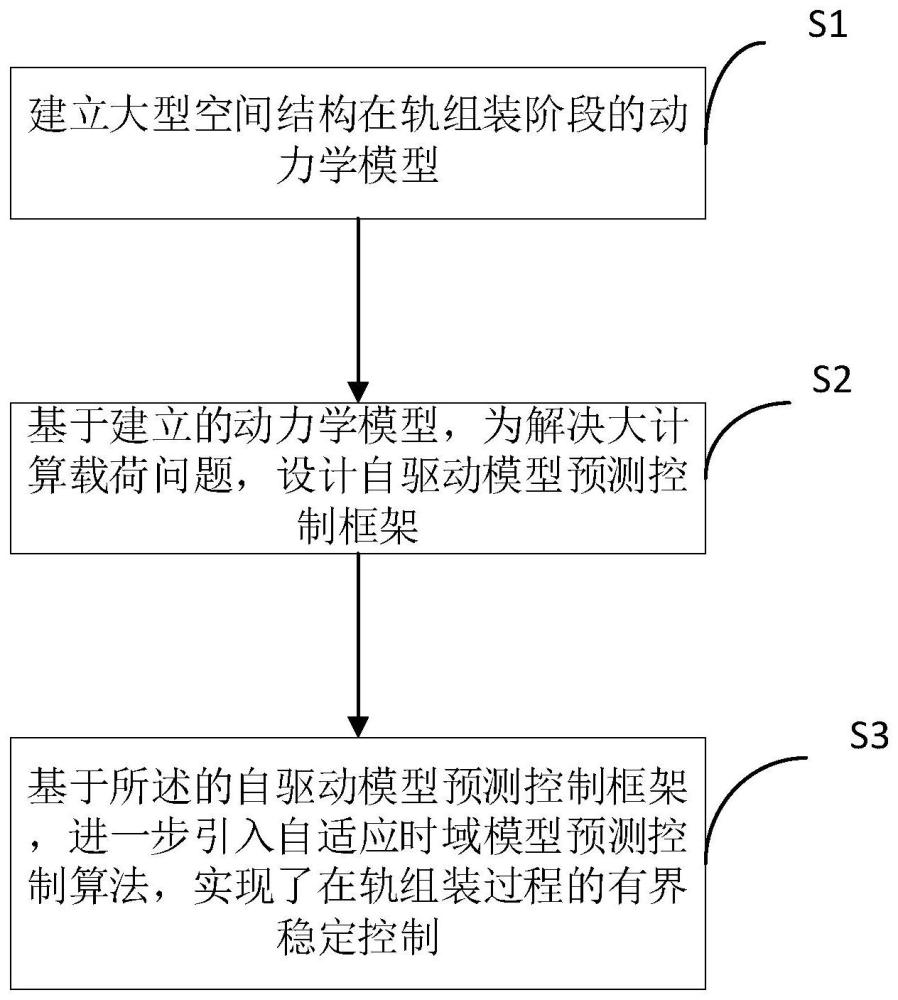
4、s1，建立大型空间结构在轨组装阶段的动力学模型；

5、s2，基于建立的动力学模型，为解决大计算载荷问题，设计自驱动模型预测控制框架；

6、s3，基于所述的自驱动模型预测控制框架，进一步引入自适应时域模型预测控制算法，实现了在轨组装过程的有界稳定控制。

7、进一步地，所述的步骤s1包括：

8、步骤s11：根据大型空间结构的运行环境，建立在轨组装阶段的动力学模型：

9、假设大型空间结构当前已组装n个模块，其中n为正整数，为了进行整体结构的建模，基于多个在轨组装模块运动模型组成的多体运动模型系统中的连通矩阵定义邻接关系向量维度为表示空间结构整体中模块i的直接邻接状态

10、

11、其中，i,j∈{1,2,…,n}，表示的第个元素，表示第i个模块的第个组装方向上与第j个模块相邻，表示第i个模块在第个方向上没有邻接的模块；的最大取值取决于模块可组装方向的个数即，为正整数，利用可进一步得到n个已组装模块的位置关系矩阵维度为n×n，是由0、1元素组成的对称方阵，的第i行第j列表示第i个模块与第j个模块有直接邻接关系，反之

12、基于模块基础模型库、以及所有已组装模块的位置关系矩阵建立当前空间结构整体的动力学模型：

13、建立n个已组装模块的组装信息库，信息库中包括各模块的组装位置信息、邻接关系向量以及各自的有限单元节点编号，当前空间结构包含的模块集合{1,2,…,n}和位置关系矩阵载入模块基础模型库；

14、进行组装建模：从模块1开始，根据和计算该模块局部坐标系os11s12s13至全局坐标系os1s2s3的坐标转换矩阵调用模块基础模型库，刚度阵与质量阵经坐标转换矩阵换算后，直接作为空间结构整体的刚度阵和质量阵接下来，根据查阅模块1的邻接模块i、计算坐标转换矩阵调用基础模型库，将其换算后的与按节点自由度在和相应位置直接扩充加载，其中组装接口共用节点位置处的刚度阵和质量阵元素是叠加后得到的，利用邻接关系向量，遍历全部己组装的模块，重复按“节点自由度”加载的步骤，可得到空间结构整体的刚度阵与质量阵单元节点信息；

15、步骤s12：按“节点自由度”的加载过程，将每个模块视为离散的“有限单元”，基于空间结构整体所包含的模块集合和邻接位置矩阵，调用模块的基础模型库，把对节点自由度有贡献的“有限单元”刚度阵和质量阵中的元素在相应位置加载，以此获得空间结构整体的刚度阵和质量阵，根据和基础模型库获得刚度阵和质量阵后，空间结构整体的动力学模型可由下式表示

16、

17、式中表示空间结构的质量阵其与矩阵和模块的质量阵相关，同理，为阻尼矩阵，x为所有的节点位移向量；为各模块控制输入叫组成的控制向量，为所有作动器的布置位置矩阵，w为组装过程中的外力扰动，为外力扰动的加载位置矩阵；考虑测量向量y，将动力学模型式转换至如下状态空间形式

18、

19、

20、其中，是测量位置矩阵；y是所有测量向量，y和分别表示位移测量向量与速度测量向量；

21、步骤s13：根据智能组件的定义，带有传感器和作动器、并集成控制算法的组装模块，具备主动感知和计算执行能力，可直接作为面向分布式控制的一个智能组件，定义主动模块i和给定范围内的邻接模块，共同作为一个智能组件并以主动模块i为核心控制模块，即以模块i的控制器和作动器作为智能组件的控制器和作动器，以模块集合{i,ji}的所有传感器作为的传感器，其中，给定范围内的邻接模块的模块邻接关系向量来获得；

22、按“节点自由度”加载的建模方法，同样适用于智能组件的动力学建模，步骤如下：

23、确认智能组件的模块集合：根据n个已组装模块的组装信息库中各模块的组装位置信息、邻接关系向量以及各自的有限单元节点编号，给定邻接范围，记录智能组件当前包含的模块集合{i,ji}，载入智能组件的组装信息库；

24、进行组装建模，将每个模块整体视为一个“有限单元”，根据智能组件包含的模块集合调用模块基础模型库，按“节点自由度”加载，得到智能组件的刚度阵与质量阵其中，和中组装接口处共同节点位置的元素也是叠加后得到的；

25、确认智能组件作动器的布置位置后，动力学模型表示为

26、

27、式中，表示智能组件的质量阵与模块的邻接关系向量和质量阵相关，同理，为的节点位移向量，为阻尼矩阵；右端为作动器布置位置矩阵，为控制输入向量，考虑结构整体对智能组件的有界作用以及的测量向量将大型在轨组装阶段的动力学模型转换至如下状态空间形式

28、

29、

30、其中，是测量位置矩阵；是模块集合{i,ji}的所有测量向量，和分别表示位移测量向量与速度测量向量；表示空间结构整体对智能组件的作用力，与结构整体的状态量x、组装过程中的扰动w和所有控制向量u相关，有界并满足如下不等式：

31、

32、其中，||·||表示向量或矩阵的欧几里德范数。

33、进一步地，所述的步骤s2包括：

34、步骤s21：基于欧拉前向差分法，将大型在轨组装阶段动力学模型离散化为如下的模型：

35、x(l+1)＝f(x(l),u(l))+w(l),x(0)＝x0,

36、其中，x(l)∈rn，u(l)∈rm和w(l)∈rn分别为在轨组装模块离散化的模型状态，控制输入及外部扰动，并假设系统受满足约束

37、

38、其中，x(l)∈rn，u(l)∈rm以及w＝{w∈rn:||w||≤η},η∈r＞0，为包含零点为其内点的紧集；

39、步骤s22：定义标称系统，并忽略外部扰动：

40、

41、其中，并且令n∈n≥1为预测时域，则需要在线优化的成本函数为：

42、

43、其中，阶段成本为终端成本为其中q＞0，p＞0和r＞0为权重矩阵；

44、步骤s23：控制目标是鲁棒地将系统状态镇定到一个包含零点的集合内，同时降低计算负荷，采用双模模型预测控制在系统状态进入终端集之前，采用自驱动模型预测控制；

45、令lj∈n为更新时间，为在kj时刻通过求解优化问题得到的最优控制序列，控制输入为：

46、

47、为了减少求解优化问题的频率，更新时间以自驱动的方式来确定，即

48、lj+1＝lj+π(x(lj)),l0＝0,

49、其中，π(·):rn→n≥1表示事件间隔时间，并在lj时刻的预测时域定义为以如下形式更新：

50、

51、其中，θ(·):rn→n表示预测时域的缩短长度，np∈n≥1为一个可以保证优化问题在初始时刻有解的常数，用πkj和θkj分别表示π(x(lj))和θ(x(lj))，保证如下形式的次优性能：

52、

53、式中，β＞1，当系统状态进入到终端集后，控制器将切换到ψ(x)来镇定系统；

54、步骤s24：建立如下的优化问题，在更新时刻lj，通过求解以下优化问题找到最优控制序列以及相应的最优状态序列：

55、

56、

57、

58、

59、

60、

61、

62、进一步地，所述的步骤s3包括：

63、步骤s31：自驱动触发机制及预测时域更新策略，触发时刻以lj+1＝lj+π(x(lj))的方式进行迭代计算，开环控制时间长度由下式给出：

64、

65、其中，

66、

67、其中，σ∈(0,1)称为性能因子；

68、步骤s32：基于所述步骤s31的分析，时域缩短长度由下式确定：

69、

70、其中，在时间段[lj,lj+1-1]内，控制量选为：

71、

72、所述自适应时域模型预测控制算法为：

73、a，判断x(lj)是否属于

74、b，若是，则利用终端控制器ψ(x)镇定系统，

75、c，若否，则执行如下步骤：

76、a)利用初始化标称系统；

77、b)求解优化问题以获得最优控制序列和最优控制轨迹

78、c)利用确定下一个更新时刻lj+1，并来确定下一个更新时刻的预测时域；

79、d)将控制序列中的前个控制量用以控制在轨组装模块的姿态角和位置状态量；

80、d，更新本发明所设计控制算法的自适应补偿参数lj，即lj+1→lj,lj∈n≥1；

81、此时完成系统的一次模型预测控制迭代过程，进而，基于在轨组装模块儿的最新系统状态，再次转到a步进行判断和控制行为的求解与动作。

82、进一步地，所述的步骤s21中系统满足如下假设条件：

83、非线性函数f(x(l),u(l)):rn×rn→rn,f(0,0)＝0,是关于x局部lipschitz连续的；

84、令g(x(l),u(l))＝f(x(l),u(l))-x(l)，则g(x(l),u(l))＝f(x(l),u(l))-x(l)也为局部lipschitz连续的，并将关于x的lipschitz常数记为lp。

85、进一步地，所述的步骤s21中参数需要满足如下假设：

86、存在一个集合可表示为并存在一个矩阵φ＞0以及一个局部控制器使得对于所有通过执行控制器可以满足如下条件：

87、

88、

89、xr可以作为标称系统的一个终端集。

90、本发明与现有技术相比，具有以下优点：

91、针对大型空间结构在轨组装阶段的振动主动控制，为进一步提升分布式控制系统的更新效率，本章基于newmark-p方法推导智能组件动力学模型的显式表达形式，结合自适应更新策略，设计了分布式自适应快速mpc控制系统，并开展了平面板式大型空间结构在轨组装阶段的数值仿真。仿真结果表明，分布式自适应快速mpc控制系统可有效抑制由组装撞击引起的空间结构整体振动，并对撞击扰动的不确定性、以及部分控制器的故障等工况具有良好的鲁棒性。自适应更新效率的分析结果表明，该系统在预测智能组件状态、以及计算控制增益矩阵时，均不涉及矩阵指数运算，与集中式快速mpc和分布式最优协同控制系统相比，其控制增益矩阵的更新时间有1至2个量级的明显提升，有效解决了在轨组装阶段分布式控制系统自适应更新效率不高的问题，且易于实现。