联合变分模态分解与时-空分数阶扩散模型的瞬变电磁信号分段滤波方法

本发明属于地球物理勘探中信号处理，特别是涉及一种联合变分模态分解与时-空分数阶扩散模型的瞬变电磁信号分段滤波方法。

背景技术：

1、瞬变电磁法是一种新兴的地球物理勘探方法，由于其勘探深度大、低阻反应灵敏、设备体积小、施工方便等优点被广泛应用于地质研究，考古勘探，资源勘探等许多领域。然而，瞬变电磁采集装置在探测过程中不可避免受到外界噪声干扰，导致有效的tem信号被淹没在强干扰背景噪声中，从而影响数据后期处理和解释，无法得到准确的地质体信息，可能导致采空区事故发生，造成经济损失和人员伤亡等影响，因此非常有必要对tem信号进行预处理。

2、各时段tem采集信号对应不同的地质体深度，前期tem信号电动势幅值大，信噪比高；中期tem信号电动势幅值迅速衰减，信噪比较低；后期tem信号电动势幅值低，信噪比低，此时信号能量微弱，噪声干扰严重。并且tem信号具有非平稳、非线性、宽频特性等特点，使得降噪处理存在一定挑战。目前常用的滤波算法，存在一些不足，比如卡尔曼滤波，小波变换，独立成分分析，广泛应用于瞬变电磁信号滤波。其中，卡尔曼滤波时，把采集tem信号当作随机信号，将状态变量与观测变量进行数据融合得到逼近真实的数据，使其作为下一个过程状态变量，并与下一过程观测变量融合，以此得到原始信号的数据。虽然该滤波方法具有一定可靠性，但需要有效信号和噪声先验信息，并且不适用于非平稳信号滤波；小波变换滤波原理是根据信号与噪声的小波分解系数不同，通过去除各频带上的噪声对应的小波系数，保留原始信号的小波分解系数，然后进行小波重构，虽能提升一定信号质量，但滤波过程中需要预先选定小波基函数和分解层数。独立成分分析降噪通过将tem信号进行线性分解，使其分离为独立统计成分，去除噪声基向量，保留有效信号，虽然，该方法具有自适应性，但算法自身的限制使得信噪分离后，与原始信号偏差较大，影响滤波结果的一致性。近年来，经验模态分解(emd)、变分模态分解(vmd)及其改进算法被应用于tem信号滤波过程中。其中，emd把信号分解成多个从高频到低频的本征模态函数，对每一个本征模态分量进行频谱分析，筛选出期望信号分量，将期望信号分量重构得到滤波信号。这种方法具有自适应性，多分辨率和多分解特性，适用于非线性、非平稳信号分解，但该方法缺乏理论基础支持，在实际应用和分解过程存在模态混叠和包络拟合偏差等问题，使得几个类似分量载波具有相似信。尽管后来一种非递归式自适应分解时间序列信号的变分模态分解方法解决了emd降噪存在的不足，并具有坚实的理论基础，鲁棒性强，避免端点效应和模态混叠问题等优点。后来，vmd和小波阈值联合的瞬变电磁信号滤波算法出现，在vmd滤波的基础上，使用小波阈值对混合模态降噪并重构有效部分得到滤波信号，信号质量得到一定改善。但是，滤波信号衰减特征不够明显，整体信号不够平滑，依然残留部分噪声干扰，并且信号后期水平波动幅度较大。因此，需要设计一种联合变分模态分解与时-空分数阶扩散模型的瞬变电磁信号分段滤波方法来解决上述问题。

技术实现思路

1、本发明所要解决的技术问题是提供一种联合变分模态分解与时-空分数阶扩散模型的瞬变电磁信号分段滤波方法，解决现有技术对整个信号滤波，没有考虑信号随地质体深度增加电动势幅度衰减率变化，造成的滤波信号存在较多奇异值，出现畸变现象，衰减特征不明显的问题。

2、为解决上述技术问题，本发明所采用的技术方案是：

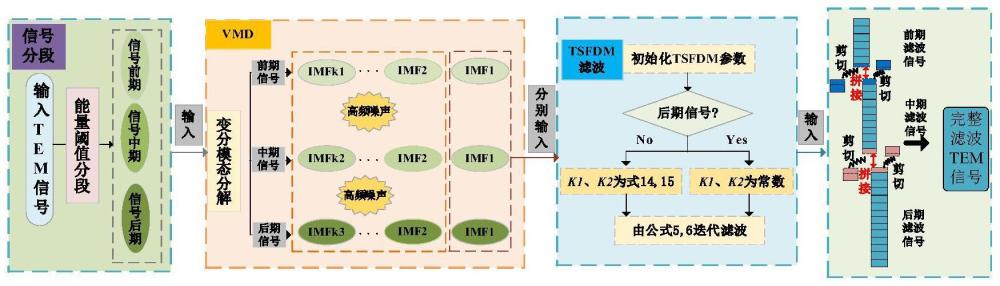
3、联合变分模态分解与时-空分数阶扩散模型的瞬变电磁信号分段滤波方法，包括以下步骤：

4、s1，由瞬变电磁法在实验区获得tem信号；

5、将tem信号转化为短时能量形式；

6、s2，通过变分模态分解vmd分别对步骤s1得到的分段信号进行滤波处理，构造增广拉格朗日函数，得到k个imf分量及其对应的中心频率；

7、s3，使用时间-空间分数阶扩散模型tsfdm对初步滤波数据做进一步平滑滤波处理；

8、s4，使用叠加平均求最值法求出tsfdm滤波器输出三段滤波信号间拼接点位置，在拼接点将信号滤波信号首尾连接，得到完整滤波信号。

9、优选地，步骤s1中，将tem信号转化为短时能量形式包括：

10、设tem信号为x(m)，对tem信号分帧加窗处理，然后对每帧tem信号平方累加得到tem信号短时能量，短时能量为：

11、

12、其中，ω(n)为海宁窗函数，p为窗长；en表示tem信号能量变化规律，设定动态阈值th和tl，en≥th时段为信号前期，th≥en≥tl时段为信号中期，en≤tl时段为信号后期；各时段信号断点处前后拓展长度为w，最终分段信号为：

13、

14、其中，w为n/200，si(1)，si(2)，si(3)分别为前、中、后期信号，x′(th)，x′(tl)为阈值th和tl对应横坐标。

15、优选地，步骤s2中，保留各时段信号imf1分量，得到tem信号初次滤波结果，分别表示为d1(1)，d1(2)，d1(3)；增广拉格朗日函数包括：

16、

17、∑kdk＝si；  (4)

18、式中，dk为vmd分解后第k个imf分量；ωk为第k个imf分量中心频率；||·||2为二范数符号；δ(t)为单位脉冲函数；*为卷积运算符；j为虚数单位；∑kdk＝si为约束条件，即imf分量之和为原输入信号si(c)；q表示惩罚因子。

19、优选地，步骤s3中，使用时间-空间分数阶扩散模型tsfdm对初步滤波数据做进一步平滑滤波处理包括：

20、在经典扩散模型基础上，利用阶次a的caputo时间分数阶导数和阶次为β的riesz空间分数阶导数分别近似整数阶偏微分方程中的时间、空间偏导数，得到时-空分数阶扩散方程：

21、

22、式(5)中，为时间caputo分数阶导数，为空间riemann-liouville分数阶导数，u(xi,tn)表示d1(c)经n次迭代滤波得到的信号；xi表示空间模板方向上第i个采样点，其中xi＝ih；tn表示时间模板方向上迭代n次，迭代层时间步长τ＝1，其中tn＝nτ；时间阶次a∈(0,1)，空间阶次β∈(1,2)；式(6)中，d1(c)表示vmd滤波后三时段tem信号；

23、g(u(xi,tn))为扩散函数，表示为：

24、

25、对式(5)中方程左端caputo时间分数阶使用差分离散，同时对式(5)中方程右端riemann-liouville分数阶导数使用带位移grunwald-letnikov逼近，建立离散差分方程，得到tsfdm滤波模型：

26、

27、式(8)表示输入信号经tsfdm滤波器第一次迭代滤波结果；式(9)表示tsfdm滤波器第n此迭代滤波将结果；bj＝(j+1)1-a-j1-a；近似为u(xi,tn)；由时间分数阶得到，相当于对历史迭代结果一种加权；平滑矩阵an和bn下所示：

28、

29、

30、式(10)和式(11)中，表示含有扩散函数的平滑矩阵权重因子；grunwald-letnikov逼近系数：g0＝1，gn＝(1-(β+1/n))gn-1；平滑矩阵系数k1、k2为非负数且k1+k2>0，平滑矩阵阶数(m-1)等于分段信号长度。

31、优选地，由于各时段tem信号电动势幅值衰减变化不一致，tsfdm处理前、中期信号时，a、b平滑矩阵系数k1、k2取值分别为如下式中的列向量：

32、

33、

34、向量中元素值呈线性递增，调节平滑矩阵中权重因子ri，以适应信号在衰减过程中信噪比减小趋势，达到较好的平滑滤波效果；在处理后期信号时，信号衰减平缓，此时k1、k2取为常数。

35、优选地，步骤s4中，使用叠加平均求最值法求出tsfdm滤波器输出三段滤波信号间拼接点位置包括：

36、

37、式中，un(1)，un(2)，un(3)分别表示前、中、后期滤波信号，i1 min表示前、中期滤波信号拼接点，i2 min表示中、后期信号拼接点；

38、计算完整信号滤波结果un：

39、

40、式(15)中，通过式(14)得到拼接点i1 min和i2 min，相邻滤波序列由拼接点首尾连接，得到完整信号滤波结果un。

41、本发明提供的联合变分模态分解与时-空分数阶扩散模型的瞬变电磁信号分段滤波方法的有益效果如下：

42、1，本发明将信号分段，以便调节各段信号滤波所需的tsfdm参数与平滑矩阵系数选取，增强算法鲁棒性；

43、2，本发明使用vmd对信号进行自适应分解，去除高频分量，用tsfdm模型抑制初次滤波信号中残留的噪声干扰，该方法具有分数阶的记忆特性，引入信号的先验信息，通过包含扩散函数的平滑算子在迭代滤波过程中考虑当前和历史信号梯度变化结果进行加权更新，滤除噪声引起的虚假梯度值，同时实现特征保护，有效解决了经验模态分解中模态混叠问题，并且滤波信号后期为纳伏特量级，信号衰减特征明显，降噪量得到提升。