一种综合约束下水下无人艇的安全轨迹跟踪控制方法

本发明涉及水下无人艇轨迹跟踪控制，具体涉及一种综合约束下水下无人艇的安全轨迹跟踪控制方法。

背景技术：

1、随着时代的进步和新兴技术的发展，复杂环境下的轨迹跟踪控制研究逐渐成为高端智能装备行业的焦点问题之一。面对复杂多变的海底环境，水下无人艇的安全轨迹跟踪控制研究在军事应用，海洋观测，海洋侦探等方面具有广泛应用前景。实际应用中，为实现各种复杂任务，在需要满足明确的运动要求外，还存在各种边界限制，例如水下无人艇穿过海峡时，不能与海峡两侧发生碰撞，即运动范围不能超过某一界限。然而，现有的控制方法只能单独处理等式约束、不等式约束，或者将不等式约束转化为等式约束进行统一处理，而无法同时独立地处理等式约束和不等式约束。

2、因此，现需要一种能够分别实现水下无人艇在等式和不等式约束下的安全轨迹跟踪控制方法。

技术实现思路

1、本发明的主要目的在于提供一种综合约束下水下无人艇的安全轨迹跟踪控制方法，以解决现有技术中的控制方法只能单独处理等式约束、不等式约束，或者将不等式约束转化为等式约束进行统一处理，而无法同时独立地处理等式约束和不等式约束的问题。

2、为实现上述目的，本发明提供了一种综合约束下水下无人艇的安全轨迹跟踪控制方法，具体包括如下步骤：

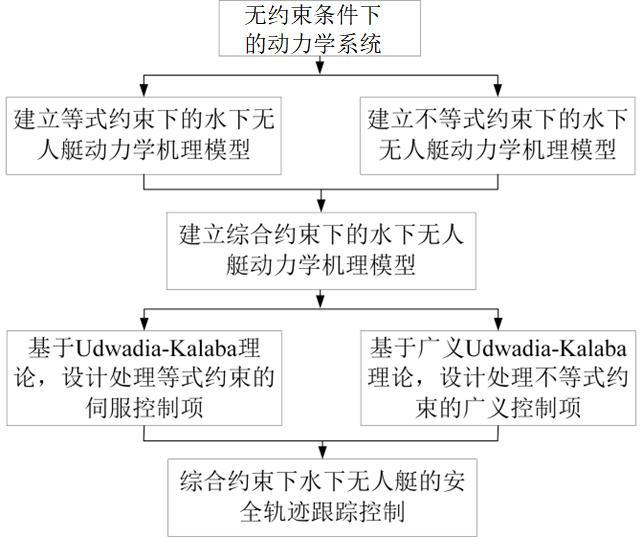
3、s1，建立等式约束下的水下无人艇动力学机理模型。

4、s2，建立不等式约束下的水下无人艇动力学机理模型。

5、s3，根据步骤s1和步骤s2，建立综合约束下，即等式约束和不等式约束下的水下无人艇动力学机理模型。

6、s4，基于udwadia-kalaba理论，设计处理等式约束的伺服控制项。

7、s5，基于广义udwadia-kalaba理论，设计处理不等式约束的广义控制项。

8、进一步地，步骤s1具体包括如下步骤：

9、s1.1，无约束条件下的动力学系统满足：

10、                 （1）；

11、其中， 为动力学系统的惯性矩阵，为正整数，表示动力学系统不受约束时受到的力，为动力学系统的广义坐标，为动力学系统的速度向量，为动力学系统的加速度向量，t表示时间。

12、s1.2，假设动力学系统受到公式（2）的约束：

13、                  （2）；

14、其中，表示第个约束，为正整数，为动力学系统的第个广义坐标，为动力学系统的第个速度向量，对公式（2）进行微分处理，则得到等式约束的一阶和二阶矩阵形式：

15、；                           （3）；

16、其中，为系数矩阵，；表示一阶微分后的常数项，表示包含二阶微分后的一阶项和常数项。

17、s1.3，基于udwadia-kalaba理论，求解等式约束力：

18、                                   （4）；

19、式（4）中，为名义部分控制力，为处理动力学系统初始条件不相容问题的控制力。

20、s1.4，根据式（1）和（4），等式约束下的水下无人艇动力学机理模型为：

21、                                      （5）。

22、进一步地，步骤s2具体包括如下步骤：

23、s2.1，假设动力学系统受到如公式（6）所示不等式的约束：

24、                      （6）；

25、式（6）中，为不等式约束的下界，为不等式约束的上界，为动力学系统在不等式约束下的实际状态，为正整数。

26、s2.2，求解不等式约束力：

27、                               （7）；

28、式（7）中，为的广义逆，是设计控制项。

29、根据式（1）、（4）和（7），动力学系统的运动学方程表示为：

30、             （8）。

31、根据式（7）有：

32、         （9）。

33、s2.3，为处理如公式（6）所示不等式的约束，进行微分同胚变换：

34、                           （10）；

35、其中，代表转换后的动力学系统状态向量，为转换函数，表示微分同胚变换过程。

36、s2.4，根据式（10），定义有界等式状态：

37、                                      （11）；

38、式（11）中，<mi>ξ=</mi><msup><mrow><mi>[</mi><msub><mi>ξ</mi><mn>1</mn></msub><mi>,</mi><msub><mi>ξ</mi><mn>2</mn></msub><mi>,...,</mi><msub><mi>ξ</mi><mi>n</mi></msub><mi>]</mi></mrow><mi>t</mi></msup><mi>,</mi><mi>ϕ=</mi><msup><mrow><mi>[</mi><msub><mi>ϕ</mi><mn>1</mn></msub><mi>,</mi><msub><mi>ϕ</mi><mn>2</mn></msub><mi>,...,</mi><msub><mi>ϕ</mi><mi>n</mi></msub><mi>]</mi></mrow><mi>t</mi></msup>。

39、s2.5，对式（11）进行求导：

40、                                       （12）。

41、s2.6，对式（12）进行求导，得到式（13）：

42、  （13）。

43、式（13）中，，<mi>ζ=</mi><msup><mrow><mi>[ξ,</mi><mover><mi>ξ</mi><mo stretchy="true">̇</mo></mover><mi>]</mi></mrow><mi>t</mi></msup>，根据式（11）和（12），进一步定义矩阵，转换后的动力学系统为：

44、   （14）；

45、式（14）中，，。

46、进一步地，步骤s3具体为：

47、根据式（1）、（5）和（7），综合约束下的水下无人艇动力学机理模型为：

48、                （15）。

49、进一步地，步骤s4具体包括如下步骤：

50、s4.1，针对如公式（5）所示的等式约束下的水下无人艇动力学机理模型，设计伺服控制项：

51、                      （16）；

52、式（16）中，为名义部分控制器，为处理初始条件不相容的控制器。

53、s4.2，基于udwadia-kalaba理论：

54、         （17）；

55、式（17）中，，对于给定的和，式（3）至少存在一个解。

56、s4.3，为处理动力学系统初始条件不相容问题，设计：

57、 （18）。

58、式（18）中，为可调参数，满秩，为可调矩阵，为动力学系统的性能误差，用于衡量系统实际状态与理想状态之间的轨迹偏差：

59、               （19）。

60、进一步地，步骤s5具体包括如下步骤：

61、s5.1，根据式（14），得到：

62、    （20）。

63、式（20）中，，控制矩阵渐进稳定，且满足lyapunov方程：

64、                              （21）；

65、式（21）中，为给定的正定矩阵，当<msub><mi>h</mi><mn>1</mn></msub><mi>=</mi><msup><mrow><mi>[0,</mi><msub><mi>h</mi><mn>1</mn></msub><mi>]</mi></mrow><mi>t</mi></msup>为赫维茨矩阵时，方程解存在且唯一。

66、令，根据式（13），分解为：

67、                                     （22）。

68、式（22）中，，即为包含大于零的项，为包含非大于零的项；存在一个已知函数：

69、                                       （23）。

70、此外，存在一个常数矩阵：

71、                                     （24）；

72、式（24）中，为可调控制参数，；其中，代表矩阵的最小特征值，是公式（23）中的已知函数，为定义的新函数。

73、根据式（20），设计控制输入项：

74、                                 （25）。

75、式（25）中，为可控设计项。

76、                             （26）。

77、本发明具有如下有益效果：

78、本发明提出一种综合约束下的水下无人艇安全轨迹跟踪控制方法。该方法基于generalized udwadia-kalabal（guk）理论，考虑具有等式约束和不等式约束的动力学系统，设计互不干扰的伺服控制项和广义控制项，分别实现动力学系统在等式约束和不等式约束下的安全轨迹跟踪控制。