视觉引导非合作移动平台飞行器动态着陆控制方法

本发明涉及飞行器控制，具体而言，涉及一种视觉引导非合作移动平台飞行器动态着陆控制方法。

背景技术：

1、飞行器可以依靠无线遥控或预先设定的飞行控制系统来执行任务，如无人机。飞行器的着陆过程往往成为事故发生的高风险时刻，因此，自主着陆的精准度和成功率至关重要，直接关系到任务的成败。目前，飞行器面临传感器的局限性、外部环境干扰以及对着陆平台的不熟悉或未知模式等挑战，在面对移动的着陆平台时，存在无法安全准确着陆的问题。

技术实现思路

1、有鉴于此，本技术实施例的目的在于提供一种视觉引导非合作移动平台飞行器动态着陆控制方法，能够改善的问题。

2、为实现上述技术目的，本技术采用的技术方案如下：

3、本技术实施例提供了一种视觉引导非合作移动平台飞行器动态着陆控制方法，所述方法包括：

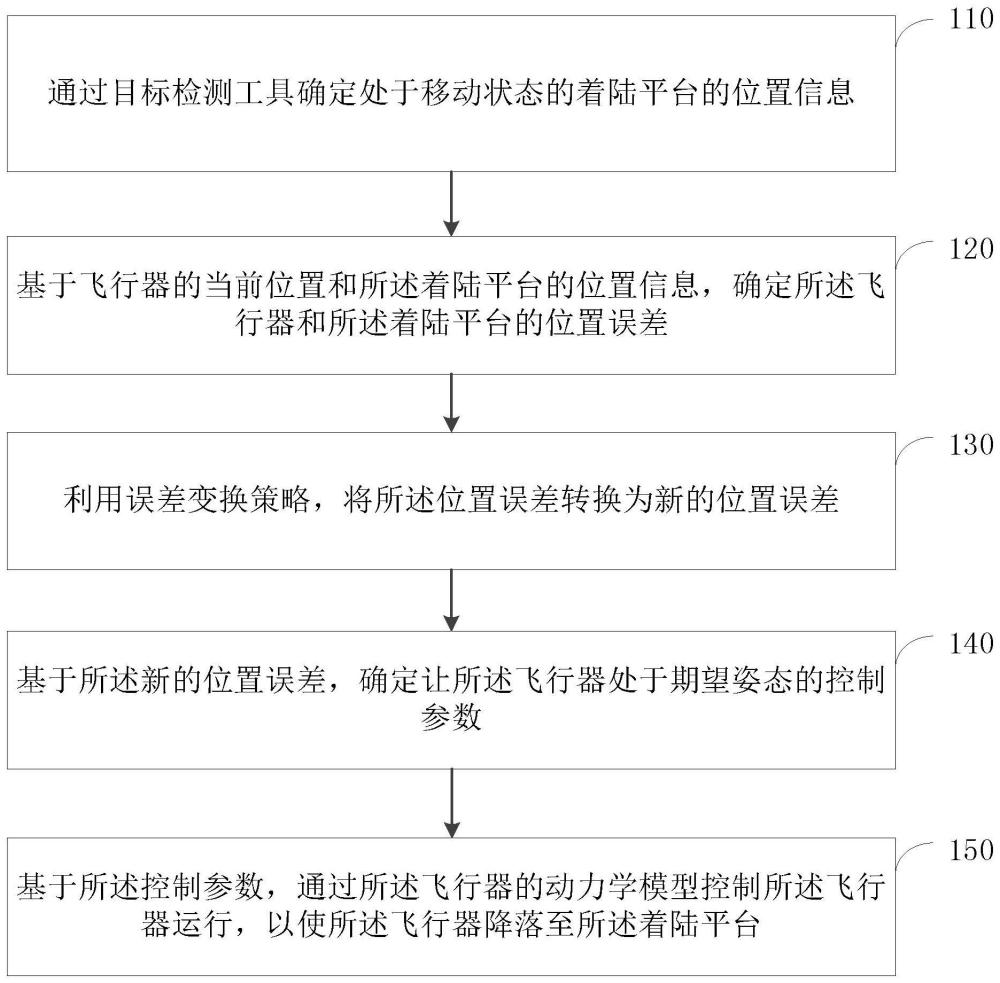
4、通过目标检测工具确定处于移动状态的着陆平台的位置信息；

5、基于飞行器的当前位置和所述着陆平台的位置信息，确定所述飞行器和所述着陆平台的位置误差；

6、利用误差变换策略，将所述位置误差转换为新的位置误差；

7、基于所述新的位置误差，确定让所述飞行器处于期望姿态的控制参数；

8、基于所述控制参数，通过所述飞行器的动力学模型控制所述飞行器运行，以使所述飞行器降落至所述着陆平台。

9、在一些可选的实施方式中，在通过目标检测工具确定处于移动状态的着陆平台的位置信息之前，所述方法还包括：

10、基于世界坐标系机体系和相机坐标系利用牛顿-欧拉公式，创建所述飞行器的动力学模型，表示为：

11、

12、

13、

14、

15、其中，ep＝[x y z]t，表示飞行器的质心位置；ev＝[vx vy vz]t，表示飞行器的速度；g＝[0 0 g]t表示重力矢量；e3＝[0 0 1]t表示一个沿z轴的单位矢量；表示从机体系到世界坐标系的旋转矩阵；表示飞行器的惯性矩阵；表示三维扭矩输入；f表示飞行器在机体系中的推力；τ表示机体系中的扭矩矢量，表示飞行器的螺旋桨的陀螺扭矩；bω＝[ωx ωy ωz]t，表示在机体系下的角速度；bω×指bω的斜对称矩阵，表示为：

16、

17、其中，ωx、ωy、ωz分别指在机体系中，x轴、y轴和z轴的角速度分量。

18、在一些可选的实施方式中，通过目标检测工具确定处于移动状态的着陆平台的位置信息，包括：

19、通过所述飞行器上安装的ros软件工具，对标记有apriltags的陆平台进行识别，得到apriltag中心在相机坐标系中的位置，记为cp；

20、对位置cp进行坐标转换，得到所述着陆平台在世界坐标系中的坐标，表示为：

21、

22、式中，指从相机坐标系到世界坐标系的旋转矩阵；是相机坐标系相对于机体系的已知固定旋转变换；为相机坐标系中的原点oc在机体系下的位置；所述着陆平台的速度记为

23、在一些可选的实施方式中，基于飞行器的当前位置和所述着陆平台的位置信息，确定所述飞行器和所述着陆平台的位置误差，包括：

24、利用误差计算公式，确定所述飞行器和所述着陆平台的位置误差ep，表示为：

25、ep＝p-pd        (7)

26、式中，p为所述飞行器的当前位置，pd为所述飞行器的期望位置，所述期望位置为所述着陆平台的位置信息。

27、在一些可选的实施方式中，利用误差变换策略，将所述位置误差转换为新的位置误差，包括：

28、利用预先创建的指定变换公式，将所述位置误差转换为所述新的位置误差，记为εp＝[εp1 εp2 εp3]t，其中，εp1 εp2 εp3分别指在三维坐标系的x轴、y轴、z轴三个方向上的误差分量；所述指定变换公式为：

29、

30、式中，εi指变换后的新的误差；ei指待变换的误差参数；ρi指性能参数；

31、所述新的位置误差的导数为：

32、

33、式中，qp＝diag(qp1 qp2 qp3)；

34、

35、

36、式中，j∈1，2，3；

37、基于反步控制算法，引入中间虚速度变量得到：

38、

39、式中，k1>0，是正参数；为与和εp对应的转换矩阵；

40、基于中间虚速度变量得到线速度误差信号ev，表示为：

41、

42、式中，ev＝[ev1 ev2 ev3]t，v指飞行器的线速度；

43、基于所述指定变换公式，对所述线速度误差信号进行变换，得到新的线速度误差，记为εv＝[εv1εv2εv3]t，其中，所述新的线速度误差的时间导数为：

44、

45、式中，qv＝diag(qv1 qv2 qv3)；

46、

47、

48、式中，j∈1，2，3。

49、在一些可选的实施方式中，在通过目标检测工具确定处于移动状态的着陆平台的位置信息之前，所述方法还包括：

50、创建所述指定变换公式。

51、在一些可选的实施方式中，创建所述指定变换公式，包括：

52、创建性能函数ρi(t)，表示为：

53、

54、式中，ρi(0)>0时，表示最大允许跟踪误差大小为正参数；初始误差为-ρi(t)≤‖ei(t)‖<ρi(0)；ρi(t)的递减速率取决于常数l，l>0；0表示稳态性能；li为一个正的常数，表示指数的衰减速率；性能函数关于时间t的数学表达式，由以下不等式表示：

55、

56、式中，ei(t)指变换前的误差；i代表不同的情况的一个下标；

57、ei(t)＝t(εi)ρi(t)       (19)

58、式中，t(εi)指误差变换函数，为新误差εi的光滑严格递增函数，且存在t(εi)对εi的反函数；t(εi)满足以下条件：

59、

60、

61、

62、选择双曲正切函数作为候选函数t(εi)，表示为：

63、

64、令基于公式ei(t)＝t(εi)ρi(t)和得到所述指定变换公式为：

65、在一些可选的实施方式中，基于所述新的位置误差，确定让所述飞行器处于期望姿态的控制参数，包括：

66、基于所述新的线速度误差，确定所述飞行器的推力f，表示为：

67、

68、其中，k2>0，为正增益；

69、从f中提取所需旋转矩阵rd＝[rd1,rd2,rd3]，得到：

70、

71、式中，a＝[cos(ψ*) sin(ψ*) 0]t；旋转矩阵rd用于计算期望的四元数qdes；

72、创建误差四元数qe，表示为：

73、qe＝q-1·qdes        (26)

74、通过以下控制律计算期望的角速度，表示为：

75、

76、基于角速度误差eω，采用反馈线性化控制策略计算期望转矩τdes，表示为：

77、τdes＝j·patteω+b ω×jb ω       (28)

78、式中，patt＝diag(pp,pq,pr)，pp,pq,pr分别为滚转、俯仰、偏航三个通道的常数增益，pp＝pq；eω＝ωdes-bω，ωdes指期望的角速度；bω指飞行器在机体系下的角速度，所述期望姿态的控制参数包括推力f、期望的角速度ωdes和期望转矩τdes。

79、在一些可选的实施方式中，基于所述控制参数，通过所述飞行器的动力学模型控制所述飞行器运行，包括：

80、将推力f、期望的角速度ωdes和期望转矩τdes输入所述飞行器的控制器，由所述控制器基于推力f、期望的角速度ωdes、期望转矩τdes和所述动力学模型，通过pwm算法对所述飞行器的电机进行控制。

81、采用上述技术方案的发明，具有如下优点：

82、在本技术提供的技术方案中，通过目标检测工具确定处于移动状态的着陆平台的位置信息；基于飞行器的当前位置和着陆平台的位置信息，确定飞行器和着陆平台的位置误差；利用误差变换策略，将位置误差转换为新的位置误差；基于新的位置误差，确定让飞行器处于期望姿态的控制参数；基于控制参数，通过飞行器的动力学模型控制飞行器运行，以使飞行器降落至着陆平台。在本方案中，用误差变换方式，处理控制过程的中间信号，可以实现低复杂度的基于位置的视觉伺服控制，使飞行器能够在运动的着陆平台上实现安全着陆。