适用于宽工况范围的高负荷涡轮损失修正模型的构建方法

本发明属于航空发动机/燃气轮机涡轮，具体的涉及一种适用于宽工况范围的高负荷涡轮损失修正模型的构建方法。

背景技术：

1、轴流涡轮作为一种叶轮式做功机械，已广泛应用于各种能源动力领域。为实现高效轴流涡轮设计，必须进行气动性能的准确预测。人们先后发展了损失预测模型、通流分析以及三维数值模拟等方法，使数值研究更贴合涡轮内部强三维非定常粘性流动。考虑到涡轮设计具有多参数非线性耦合特点，并且设计流程需要精细、反复调整，损失预测模型显得尤为重要，可以为低维仿真、优化和设计提供重要指导，并大大缩短研发周期。通常涡轮损失估算有四种方法，分别为采用损失模型估算损失、根据已有的损失数据估算损失、通过数值模拟估算损失以及通过实验估算损失，其中，采用损失模型估算损失可以大幅度节省时间，因而国内外诸多学者在损失模型的建立，修正和完善过程中做了大量的工作并取得了一定的成果。然而不同的损失模型预估的准确性和结果不同，所以有必要对损失模型进行研究，找到适合的损失模型或者是恰当的修正方法，以提高损失模型预估的准确性，以期可以快速而准确的预估损失，同时还可以通过已有的损失数据，或者通过数值模拟和实验的方法对原有的损失模型进行修正。

2、但现有的各种损失模型在基本假设、计算方法、损失预测精度和适用范围等方面都存在差异，有研究表明不同损失模型的选择对优化设计结果造成很大影响。而传统模型本身在高负荷宽工况涡轮的适应性就不好。因此追求更准确、适用性更好的高负荷宽工况涡轮的损失预测方法一直都是国内外学者研究的重点课题。

3、如叶栅kacker-okapuu(k-o)模型，是一个用于预测和分析涡轮机叶片通道内部流动损失的经验模型。这个模型由ajay kacker和marko okapuu提出，主要用于气体涡轮发动机中叶片的气动设计和优化过程。k-o模型能够为设计师提供一个相对简单且有效的工具，以评估不同设计变量对叶栅气动性能的影响，尤其是在预测叶片通道内部的总压损失方面。k-o模型基于大量的实验数据和经验关系，通过考虑叶片几何形状、流动条件(如雷诺数和马赫数)以及叶栅配置(比如叶片间距、攻角等)的影响，来估计流动损失。它特别适用于初步设计阶段，当需要快速评估不同设计方案时，可以提供有用的指导和参考。模型的核心在于它能够合理简化复杂的流动现象，使得在没有进行完整的数值流体动力学(cfd)模拟的情况下，也能够对叶栅的气动性能进行初步的评估。然而，需要注意的是，虽然k-o模型在工业界广泛应用，但它仍然是一个基于经验的模型，其准确性依赖于模型参数的选取和适用范围。

4、可见单就叶型损失来说，传统损失模型在高负荷宽工况涡轮的范围内适用性并不好，这是由于高负荷宽工况涡轮的损失与传统涡轮的损失存在差异。因此关于攻角修正的高负荷宽工况涡轮叶型损失修正模型迫在眉睫。

技术实现思路

1、为克服上述现有技术的不足，本发明提供了提出了一种适用于宽工况范围的高负荷涡轮损失修正模型的构建方法，基于现有的实验数据，通过增加修正因子，着重修正了攻角对损失的影响，完善和改进传统的ko模型，实现更精确预测涡轮的气动性能。

2、本发明为解决其技术问题所采用的解决技术方案为：

3、本发明的一种适用于宽工况范围的高负荷涡轮损失修正模型的构建方法，包括以下步骤：

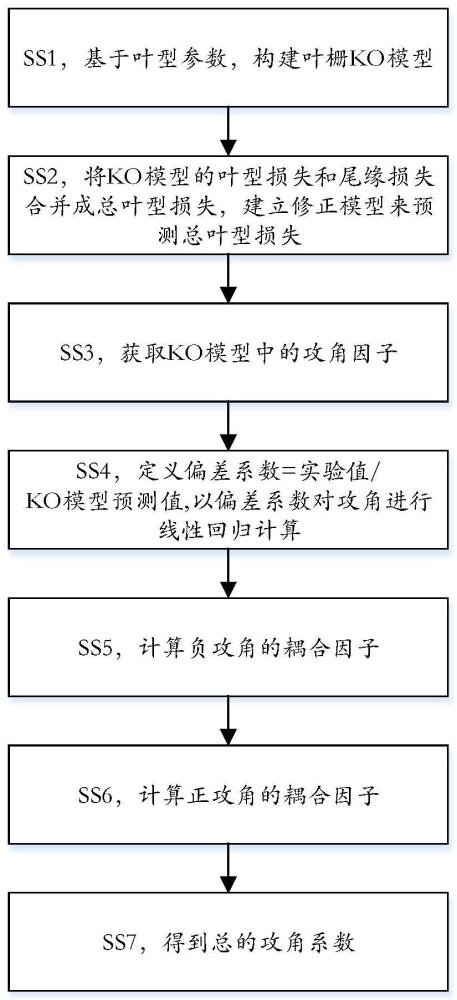
4、ss1，基于叶型参数，构建叶栅ko模型，如公式(1)所示：

5、

6、其中,yp为ko模型的叶型损失，χi为ko模型的攻角修正因子；y′p,am是am模型中的叶型损失，kp是马赫数修正因子，yshock是激波损失，y′tet是尾缘损失；

7、ss2，将ko模型的叶型损失和尾缘损失合并成总叶型损失，建立修正模型来预测总叶型损失，如公式(2)所示：

8、

9、其中，yp是修正模型的总叶型损失，k′p是新修正的马赫数因子，χ′i是修正模型的攻角修正因子，χ′re是修正模型的雷诺因子；

10、ss3，获取ko模型中的攻角因子，如公式(3)所示：

11、

12、ss4，定义偏差系数＝实验值/ko模型预测值,以偏差系数对攻角进行线性回归计算，如公式(4)所示：：

13、χ＝-4×105×(i)3-0.0019×(i)2+0.031×i+2.1408(i<0)  (4)

14、ss5，计算负攻角的耦合因子：观察残差的情况，发现负攻角已经基本稳定，和雷诺数已经没有关系，实现了解耦，只和正攻角和负攻角攻角有关，因此残差对正攻角和负攻角再进行回归，得到负攻角的耦合因子，如公式(5)所示：

15、

16、ss6，计算正攻角的耦合因子：正攻角的残差仍然随着雷诺数和攻角同时变化,因此先对雷诺数回归，观察到re<50k和re>50k的耦合因子相差较大；因此分成两类后，再以残差对对正攻角和负攻角再回归一次，如公式(6)和(7)所示：

17、

18、

19、ss7，得到总的攻角系数，如公式(8)所示：

20、

21、优选的，其中，步骤ss3中获取ko模型中的攻角因子的过程为：

22、α1是进口气流角，β1是进口金属角，α2是出口气流角，β2是出口金属角，s指的是栅距，c指的是弦长；

23、以55<α1<60为例，

24、

25、

26、

27、i＝is+δis。

28、优选的，步骤ss2中的叶型损失和尾缘损失合并成叶型损失的过程中，引入了叶型因子，其中包括对尾缘损失的修正。

29、优选的，步骤ss4中定义的偏差系数是通过最小二乘法对实验数据和ko模型预测值进行线性回归分析得到。

30、优选的，步骤ss5中计算负攻角的耦合因子时，进一步包括对残差进行分析以确定负攻角的稳定性，并基于此确定负攻角与雷诺数的解耦关系。

31、优选的，步骤ss6中计算正攻角的耦合因子时，进一步包括根据雷诺数的不同范围对正攻角的残差进行分类，并分别对不同雷诺数范围内的残差进行回归分析，以得到适用于不同雷诺数范围的正攻角耦合因子。

32、优选的，步骤ss4进一步包括以下步骤：

33、ss41、收集一系列实验数据，包括在不同工况下的涡轮叶型损失值。并通过ko模型中的公式计算出ko模型的预测值；

34、ss42、利用最小二乘法对实验数据和ko模型预测值进行线性拟合，以确定线性回归方程中的系数；

35、ss43、在进行线性回归分析时，考虑到实验数据可能存在的误差和偏差，采用加权最小二乘法对数据进行处理，以提高回归方程的准确性和可靠性；

36、ss44、得到描述实验值与ko模型预测值之间关系的数学模型，该模型能够量化两者之间的偏差，即偏差系数；

37、ss45、利用得到的偏差系数对原有的ko模型进行修正，以便更准确地预测在宽攻角条件下涡轮叶型的损失。

38、本发明与现有技术相比所具有的优点：

39、(1)本发明针对高负荷宽工况涡轮叶型损失的修正模型，能够在宽雷诺数和宽攻角的条件下，更精确地预测涡轮的损失。传统的涡轮损失模型在高负荷宽工况下的适用性有限，而本发明通过引入修正因子和耦合因子，显著提高了预测的准确性。

40、(2)本发明的模型不仅适用于常规的涡轮设计条件，还能够应对极端工况，如高攻角和高雷诺数的情况。这种广泛的适用性使得本发明的模型在不同类型的涡轮设计中都具有很高的实用价值，可应对多变的设计挑战。

41、(3)通过本发明的修正模型，可以更准确地预测涡轮的气动性能，有助于减少设计迭代次数，缩短研发周期，降低成本，并最终提高涡轮的整体性能和效率。

42、(4)本发明通过对攻角和雷诺数耦合影响的深入分析，提供了对涡轮叶型损失机理更深层次的理解。这种理解有助于指导未来的研究方向，推动涡轮气动设计理论的发展，并为新型涡轮的设计提供理论基础。

43、(5)本发明在构建修正模型的过程中，充分利用了现有的实验数据。通过最小二乘法和线性回归分析，本发明能够有效地从实验数据中提取有用的信息，并将其转化为模型的修正参数。通过对实验数据的有效利用，提高了模型的准确性。

44、(6)本发明的模型特别考虑了攻角和雷诺数的耦合效应对涡轮叶型损失的影响。通过分别计算负攻角和正攻角的耦合因子，本发明能够更准确地描述这种耦合效应，并将其纳入损失预测中。