一种方程式赛车转向梯形机构的优化方法

：本发明专利涉及方程式赛车，具体为一种方程式赛车转向梯形机构的优化方法。

背景技术

0、背景技术：

1、formu1a sae(fsae)是一项面向大学生的综合性工程教育赛事，自1978年开办以来，距今已有40多年时间，赛事遍及美国、加拿大、德国、中国等国家。中国大学生方程式系列赛事创立于2009年，创立至今，中国大学生方程式系列赛事已经发展为fscc、fsec、bsc、fsac四个分赛项目。近年来，越来越多的高校参与到该赛事中，该赛事为中国汽车工业培养了大量人才。对于任何一项fsae赛事，都需要设计一套结构简单且满足比赛需求的转向系统，以保证赛车具有良好的操纵稳定性与过弯能力。

2、转向梯形机构是转向系统中的主要传动机构，常见的转向梯形机构有整体式转向梯形机构、齿轮齿条式转向机构，方程式赛车通常采用齿轮齿条式转向机构，齿轮齿条式转向梯形机构由转向横拉杆、梯形臂、齿轮齿条转向器中的齿条和前桥组成，属于断开式转向梯形机构。根据齿轮齿条式转向器和转向梯形相对前轴位置的不同，分为后方后置、后方前置、前方后置和前方前置四种布置形式。转向梯形机构设计的好坏直接影响了赛车的转向性能，为了减小转向梯形机构设计的误差，提高赛车的转向性能，有必要对转向梯形机构进行优化设计。

3、目前，对转向梯形机构的优化设计研究已经取得了很多成果。在转向梯形的确定性优化设计研究中，翟建华等使用改进的粒子群算法对转向梯形进行了优化设计，李子朋等基于免疫算法对断开式转向梯形进行了优化设计，这些优化算法在转向梯形的确定性优化设计中都得到了验证，优化后的转向梯形与目标阿克曼转向模型的吻合度很高。然而，转向梯形机构在制造、加工和安装的过程中存在大量的不确定性，梯形参数的细微偏差都会对转向系统的性能产生影响。因此，采用考虑不确定性因素的转向梯形稳健性优化设计方案更符合工程实际。史天泽等基于6σ稳健性对电动汽车断开式转向梯形进行了优化设计，结果表明，稳健性优化结果比确定性优化结果具有更高的稳健性和可靠性。对于大部分方程式赛车车队，由于条件的限制，转向梯形机构的装配、安装过程都只能借助一些简单的定位夹具，梯形参数的偏差和波动会较大。因此，在方程式赛车转向梯形的优化设计过程中需要考虑到梯形参数的不确定。目前，针对系统模型的稳健性优化设计方案通常都是在确定性优化的基础上进行的，即在确定性优化结果的基础上使用梯度下降法等局部搜索优化算法进行稳健性优化。对于转向梯形这样复杂的非线性模型，基于确定性优化结果的局部搜索优化算法的稳健性优化设计方案有时并不能得到一个理想的解，使得转向梯形稳健性优化还存在优化不佳的问题。

技术实现思路

0、技术实现要素：

1、本发明的的目的是为了克服现有技术的不足，提出一种方程式赛车转向梯形机构的优化方法，对方程式赛车转向梯形的参数进行稳健性优化设计，在保证转向梯形符合目标阿克曼转角关系的前提下，具有更高的稳健性和可靠性。

2、第一方面，本发明提供一种方程式赛车转向梯形机构的优化方法，其包括以下步骤：

3、步骤一、获取转向梯形机构的已知参数。

4、步骤二、构建确定性优化模型和稳健性优化模型。

5、步骤三、对转向梯形机构被优化的各个设计参数进行sobol灵敏度分析，并将各个设计参数按照灵敏度从大到小排序。

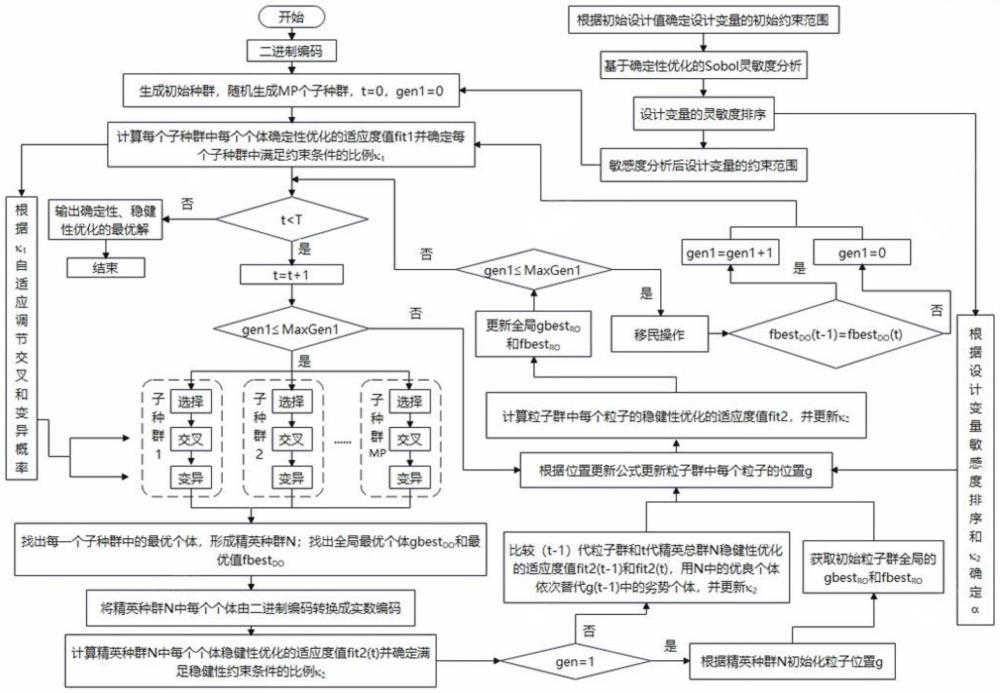
6、步骤四、对转向梯形机构同时进行确定性优化和稳健性优化。利用多种群遗传算法进行确定性优化获得精英种群，并为粒子群算法提供初始化粒子群；利用粒子群算法进行稳健性优化；迭代过程中精英种群中的精英个体迁移到粒子群中替换劣势个体。

7、多种群遗传算法中，每个子种群在交叉、变异操作中使用的交叉概率pc和变异概率pm根据子种群中满足确定性优化模型约束条件的比例k1调整。

8、粒子群算法中，更新粒子群位置时强度缩放系数α根据子种群中满足稳健性优化模型约束条件的比例κ2调整。

9、步骤五、取步骤四得到的全局最优个体中的值作为转向梯形机构的各个设计参数的优化结果。

10、作为优选，交叉概率pc和变异概率pm的表达式如下：

11、

12、其中，ρ1和ρ2为交叉概率pc和变异概率pm的自适应调节因子；pcmin和pcmax分别为最小交叉概率、最大交叉概率；pmmin和pmmax分别为最小变异概率和最大变异概率。

13、作为优选，强度缩放系数α的表达式如下：

14、

15、其中，φj为自适应随机性强度缩放控制因子，取值范围为(0，l0]；四个设计参数对应的φj从大到小的排序与敏感度从大到小的排序一致。

16、作为优选，步骤四的具体过程如下：

17、4-1.生成包括mp个子种群的初始种群；mp为子种群数目；初始化局迭代次数t；种群迭代序数gen1。

18、4-2.计算每个子种群中每个个体确定性优化的适应度值fit1，并确定每个子种群中满足确定性优化模型约束条件的比例κ1。

19、构建确定性优化的适应度函数为：

20、fit1(x)＝fdo(x)+χsum(|g′i(x)|)

21、

22、其中，fdo(x)为确定性优化模型的目标函数；χ为惩罚因子；ζ为精度控制因子。gi(x)为确定性优化模型中的约束条件。

23、4-3.若满足终止判断条件，则终止迭代，输出确定性和稳健性优化的最优解。其中，t为最大迭代次数；否则，将t增大1。终止判断条件为：t≥t。

24、4-4.若gen1≤maxgen1，执行步骤4-5；否则，停止确定性优化，直接执行步骤4-9。其中，genmax1为最优解保持代数。

25、4-5.每一个子种群分别进行选择、交叉、变异操作。

26、4-6.找出每一个子种群中的最优个体，形成精英种群；找出全局最优个体gbestdo和最优值fbestdo。

27、4-7：计算第t代精英种群n中每个个体稳健性优化的适应度值fit2(t)，并确定精英种群中满足稳健性优化模型约束条件的比例k2。构建稳健性优化的适应度函数为：

28、fit2(x)＝fro(x)+χsum(|g′i(x)|)  (23)

29、

30、其中，fro(x)为稳健性优化模型的目标函数；

31、4-8：判断。若t＝1，根据精英种群初始化粒子群位置；将粒子群代入稳健性优化模型，获取初始粒子群中的全局最优个体gbestro和全局最优值fbestro；否则，比较第(t-1)代粒子群和第t代精英种群稳健性优化的适应度值fit2(t-1)和fit2(t)；用第t代精英种群中的优良个体依次替换第(t-1)代粒子群中的劣势个体，得到更新后的第(t-1)代粒子群。

32、4-9.更新得到第t代粒子群的位置如下：

33、

34、其中，分别为第t、(t-1)代粒子群位置；p的取值为0.1～0.7；∈d为服从均值为0，标准差为1的正态分布的d维随机向量；d等于设计变量的个数；

35、4-10.计算第t代粒子群中每个粒子的稳健性优化的适应度值fit2，并更新比例κ2。

36、4-11.将第t代粒子群代入稳健性优化模型，获取第t代粒子群中的全局最优个体gbestro和全局最优值fbestro。

37、4-12.在gen1≤maxgen1的情况下，执行移民操作，若第t代粒子群的fbestdo(t)等于第(t-1)代粒子群的fbestdo(t-1)，则将gen1增大1，否则gen1＝0。之后重新执行步骤4-2至4-11，直到满足步骤4-3终止判断条件。

38、在gen1>maxgen1的情况下，则重新执行步骤4-3至4-11，直到满足步骤4-3终止判断条件。

39、作为优选，设计参数共有四个，分别为梯形臂长度r、梯形底角λ、齿条拉杆长度m、齿条轴线与k线之间的距离h。

40、作为优选，步骤三中sobol灵敏度分析的过程如下：

41、步骤3-1.采用准随机sobol序列进行采样，对设计参数进行2p次抽样，生成2个p×d的输入矩阵，分别为矩阵a和b；其中，p为采样点数；d为设计参数的个数。

42、步骤3-2.用矩阵b中的第i列替换矩阵a中的第i列，构造p×d的矩阵abi，i＝1，2，...，d；得到d+2个样本矩阵，将d+2个样本矩阵代入确定性优化模型中进行计算，可以得到d+2个输出向量。

43、步骤3-3.根据步骤3-2求取的d+2个输出向量求取各设计参数对应的第1阶灵敏度指数和总阶灵敏度指数，并对各设计参数进行排序。

44、作为优选，步骤一采集的己知参数包括轴距l、两主销与转向梯形平面交点的距离k、最大外轮转角θomax、阿克曼率ra、许用齿条行程[δm]。

45、作为优选，所述的确定性优化模型如下：

46、minimize fdo(r，λ，h，m)

47、subjectto

48、

49、其中，g1(x)、g2(x)、g3(x)分别为三个约束值，其表达式为g1(x)＝δmmax-[δm]、δmmax为最大齿轮行程；[δm]为许用齿条行程；r为梯形臂长度；λ为梯形底角；m为齿条拉杆长度；h为齿条轴线与k线之间的距离；θimax为内轮最大转角；n为横拉杆长度。

50、作为优选，所述的稳健性优化模型如下：

51、minimize fro＝ημ(δ∈)+(1-η)σ(δ∈)

52、subjectto

53、

54、其中，η为权重系数；μ(δ∈)和σ(δ∈)分别为优化目标的均值和标准差；μ[gi]、σ[gi]分别为约束值gi(x)的均值和标准差；σ(n)为横拉杆长度的标准差；n为横拉杆长度。

55、第二方面，本发明提供一种方程式赛车转向梯形机构，其通过前述的优化方法得到。

56、与现有技术相比，本发明的有益效果为：

57、1.针对方程式赛车转向梯形机构优化问题，基于种群中满足约束条件的比例，在标准遗传算法sga和多种群遗传算法mpga中引入了自适应调节的交叉概率和变异概率，提出了aga、ampga算法，改进后的标准遗传算法和多种群遗传算法在方程式赛车转向梯形机构优化时具有更高的全局寻优能力和收敛性能，提出的ampga算法在多种群少个体的情况下依旧具有较高的全局寻优能力；

58、2.针对方程式赛车转向梯形机构优化问题，基于sobol灵敏度分析结果和粒子群体中满足约束条件的比例，在apso算法引入了自适应随机性强度缩放参数，提出了改进的apso算法apso ii，改进后的apso算法在方程式赛车转向梯形机构优化中具有更高的全局寻优能力，能够有效的避免陷入局部最优解；

59、3.针对方程式赛车转向梯形机构的稳健性优化问题，在上述改进的优化算法ampga和apso ii的基础上，提出了一种ampga-apso ii的方程式赛车转向梯形机构稳健性优化设计方法，ampga-apsoⅱ算法可以同时求出方程式赛车转向梯形机构确定性和稳健性优化设计的结果，ampga算法用于求解确定性优化的结果，apsoⅱ算法用于求解稳健性优化的结果。ampga-apsoⅱ算法的两部分并不是独立执行的，在ampga算法执行的确定性优化部分与apsoⅱ算法执行的稳健性优化部分存在一定的联系，ampga算法为apsoⅱ算法提供精英初始化粒子群，在迭代进化过程中ampga算法将优良个体迁移到apsoⅱ算法的粒子群中替换掉apsoⅱ算法中的劣势个体，可以有效的提升稳健性优化的全局寻优能力，有效的避免出现早熟收敛和陷入局部最优解的情况。与一般的稳健性优化方法相比，基于ampga-apsoⅱ算法的方程式赛车转向梯形机构的稳健性优化结果具有更高的稳健性和可靠性。