一种基于顶装式旋转激光定位系统的坐标系标定方法

本发明属于电子信息标定，涉及一种坐标系标定方法，具体涉及一种基于顶装式旋转激光定位系统的坐标系标定方法。

背景技术：

1、本背景技术提供的仅仅是与本发明相关的背景信息，其并不必然构成现有技术。

2、激光定位系统在大型工业测量领域得到广泛应用，而激光定位系统的多台激光发射站的坐标的统一化是当前激光定位系统所面临的关键技术问题。

3、目前最常见的坐标统一方法是采用标准尺法。该方法利用已知长度的标准尺摆放在测量空间的多个位置上，通过基于标准尺的长度约束求解标准尺两端接收器的坐标，从而通过坐标的转换来实现激光发射站的坐标系的统一。

4、然而，当前标准尺法为了达到较高的标定精度，需要将标准尺分布在测量空间的多个位置。以一个空间尺寸为3.5m×4.0m×2.0m的区域为例，在距离两激光发射站约6m远的位置，就需要使用16个参考位置才能将尺长测量误差控制在0.25mm以内。因此，该方法效率较低。

5、鉴于当前技术的上述不足，迫切需要研发一种新型的激光定位系统坐标统一化方法。

技术实现思路

1、本发明旨在克服现有技术的缺陷，提供一种基于顶装式旋转激光定位系统的坐标系标定方法，旨在提高原始激光发射站的坐标统一的效率。

2、为了实现上述目的，本发明提供如下技术方案：

3、一种基于顶装式旋转激光定位系统的坐标系标定方法，其特征在于，包括以下步骤：

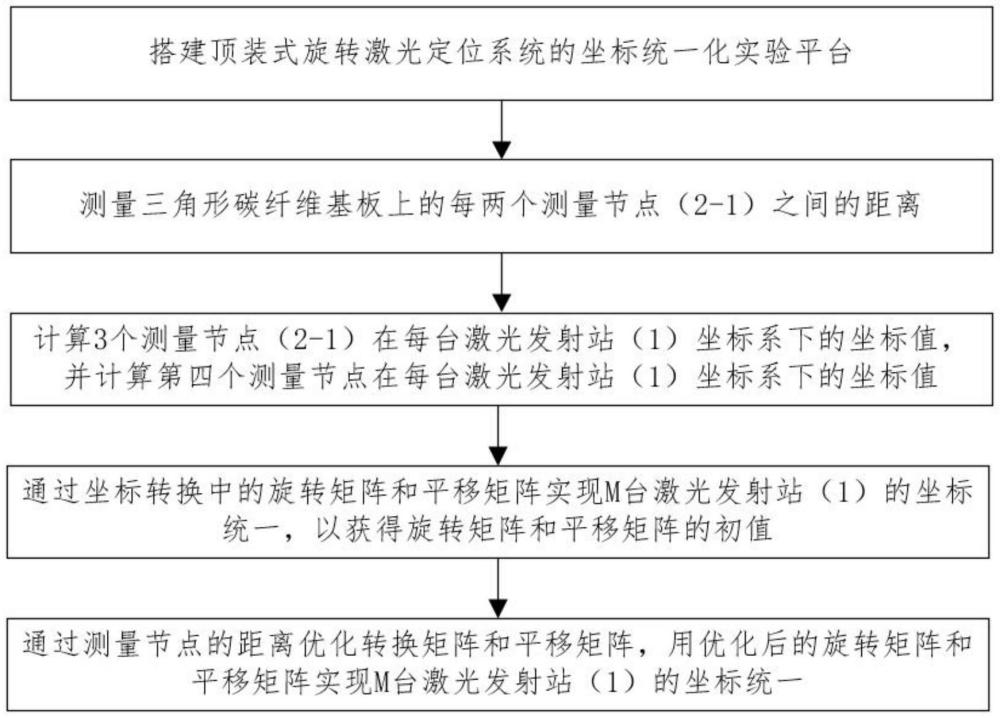
4、1)搭建顶装式旋转激光定位系统的坐标统一化实验平台，所述坐标统一化实验平台包括m台激光发射站和一个标定板，其中，m≥2，所述标定板设置在所述m台激光发射站的公共可视范围内且所述标定板包括三角形碳纤维基板和固定于所述三角形碳纤维基板上的3个测量节点；

5、2)利用测量距离仪器测量所述三角形碳纤维基板上的每两个所述测量节点()之间的距离；

6、3)用所述m台激光发射站分别测量3个所述测量节点在每台所述激光发射站的坐标系下的俯仰角，并结合步骤2)测量的距离计算出3个所述测量节点在每台所述激光发射站的坐标系下的坐标值，且基于3个所述测量节点在每台所述激光发射站的坐标系下的坐标值计算出第四个测量节点在每台所述激光发射站的坐标系下的坐标值；

7、4)根据4个所述测量节点在每台所述激光发射站的坐标系下的坐标值，通过坐标转换中的旋转矩阵和平移矩阵实现所述m台激光发射站的坐标统一，以获得所述旋转矩阵和平移矩阵的初值；

8、5)通过所述测量节点的距离优化所述转换矩阵和平移矩阵，用优化后的旋转矩阵和平移矩阵实现所述m台激光发射站的坐标统一。

9、优选地，所述步骤1)中，所述顶装式旋转激光定位系统的坐标统一化实验平台的公共可视范围为椭圆测量场区，在所述椭圆测量场区内放置所述标定板，所述三角形碳纤维基板的三个角各固定一个所述测量节点，分别记为a1、a2、a3。

10、优选地，所述步骤2)中，利用测量距离仪器分别测量所述标定板的测量节点a1、a2、a3之间的距离，其中，测量节点a1和a2之间距离记为l12、测量节点a1和a3之间的距离记为l13，测量节点a2和a3之间的距离记为l23。

11、优选地，所述步骤3)具体为：

12、3.1)将所述标定板放置在所述椭圆测量场区内，其中一台所述激光发射站扫描到所述测量节点时，当前所述激光发射站的两个扇面激光在各个测量节点a1、a2、a3处分别交汇成一条从当前所述激光发射站到各个测量节点a1、a2、a3的射线，获得当前所述激光发射站到测量节点a1与a2的射线的夹角α1、到测量节点a1与a3的射线的夹角β1、到测量节点a2与a3的射线的夹角γ1；

13、3.2)将当前所述激光发射站到各个测量节点a1、a2、a3的距离分别设为s11、s12、s13，结合已知的距离l12、l23、l13，再由余弦定理计算出s11、s12、s13；

14、3.3)根据各个测量节点a1、a2、a3之间的距离l12、l23、l13，以及当前所述激光发射站到各个测量节点a1、a2、a3的距离s11、s12、s13，计算出各个测量节点a1、a2、a3在当前所述激光发射站的坐标系下的坐标值；

15、3.4)根据各个测量节点a1、a2、a3在当前所述激光发射站的坐标系下的坐标值，得到向量另设一点q为第四测量节点，且点q满足以下公式：

16、

17、计算得到对其单位化，设为最终可以得到第四个测量节点a4及其在当前所述激光测量站的坐标系下的坐标值；

18、3.5)重复上述步骤3.1)-3.4)，得到四个所述测量节点a1、a2、a3和a4在每台所述激光发射站的坐标系下的坐标值。

19、优选地，所述步骤4)具体为：

20、四个测量节点a1、a2、a3和a4可列公式(1)，共4个方程，由于每个测量节点的坐标值都是三维的，因此，每个方程根据三维坐标，又可以分成3个方程，因此，将有12个线性方程，然而旋转矩阵r有9个未知数，平移矩阵t有3个未知数，12个方程能够用最小二乘法求解旋转矩阵r和平移矩阵t的近似值，即，解算出旋转矩阵r和平移矩阵t的初值，

21、

22、式中，a11、a21、a31和a41分别表示测量节点a1、a2、a3和a4在第1号激光发射站的坐标系下的坐标值；a12、a22、a32和a42分别表示测量节点a1、a2、a3和a4在第2号激光发射站的坐标系下的坐标值。

23、优选地，所述步骤5)具体为：

24、5.1)将所述标定板放置于所述m台激光发射站的公共可视范围内的n个位置上，其中，在每个位置上，用每台所述激光发射站分别测量所述三角形碳纤维基上的测量节点；

25、5.2)确定所述标定板在第n个位置时第m台激光发射站扫描到第i个测量节点时的距离约束为：

26、

27、式中，[ankm bnkm cnkm dnkm](k＝1,2)为所述标定板在第n个位置时第m台激光发射站的第k个激光平面扫到坐标为ani的测量节点时的平面系数；rtxgk和ttxgk为全局坐标系到第k台激光发射站的坐标系的旋转矩阵和平移矩阵；

28、5.3)确定所述标定板在第n个位置时第i个测量节点与第j个测量节点之间的距离约束为：

29、dnij＝||anianj||-lij (3)

30、式中，dnij表示所述标定板在第n个位置时第i个测量节点与j个测量节点的测距误差，||aiaj||表示所述标定板在第n个位置时第i个测量节点与j个测量节点之间的欧式距离，lij表示所述标定板在第n个位置时第i个测量节点与j个测量节点之间的测量距离；

31、5.4)确定第m台激光发射站的坐标系到全局坐标系的旋转矩阵的正交约束为：

32、

33、其中，旋转矩阵r表示为的形式，m＝1,2,...,m，其为第m台激光发射站的坐标系到全局坐标系的旋转矩阵，p、q是旋转矩阵r中的行标；

34、5.5)联合以上约束，建立优化目标函数为：

35、

36、5.6)将解算出的旋转矩阵r和平移矩阵t的初值作为所述优化目标函数的迭代初值，根据非线性优化算法迭代求解上述优化目标函数，以获得旋转矩阵r和平移矩阵t的最优解，并用所述旋转矩阵r和平移矩阵t的最优解进行坐标系的标定；

37、其中，n＝1,2,...,n表示所述标定板移动到第n个位置，m＝1,2,...,m表示第m台激光发射站，k＝1,2表示激光发射站的第k个激光扇面，i＝1,2,3表示所述标定板中的第i个测量节点。

38、优选地，n≥9。

39、与现有技术相比，本发明的基于顶装式旋转激光定位系统的坐标系标定方法具有如下有益技术效果中的一者或多者：

40、1、本发明使用带有三个测量节点的三角形碳纤维基板作为标定板，标定时需要保证每个激光发射站可以扫描测量节点，无需对标定板的姿态有任何要求，但是需要求取第四个点的坐标，避免了求解坐标转换关系时，线性方程组的系数矩阵不满秩的情况。

41、2、本发明在求解激光发射站的坐标系的转换关系时，通过在标定板放置更多的参考位置，系统标定的精度呈正相关，但是若太多位置会增加计算速度，因此在一个6m×5m×2m的测量区域内，将标定板移动至9个不同的参考位置进行3台激光发射站的标定，长度测量的平均误差保持在不大于0.224mm的范围内。

42、3、本发明无需对标定板的摆放位姿有任何要求，既可以实现顶装式旋转激光定位系统的坐标系标定，并且随着标定板移动位置的增加，坐标统一化的精度也随之提高，从而提高了坐标统一的效率。