一种塑性起始点的计算方法及装置与流程

本发明涉及塑性材料测试，尤其涉及一种塑性起始点的计算方法及装置。

背景技术：

1、弹塑性固体材料在受力后产生变形，从变形开始到破坏一般要经历弹性变形和塑性变形这两个阶段。根据材料力学性质的不同，有的弹性阶段较明显，而塑性阶段很不明显；有的则弹性阶段很不明显，从开始变形就伴随着塑性变形，弹塑性变形总是耦连产生。而大部分固体材料都呈现出明显的弹性变形阶段和塑性变形阶段。在工程分析及材料应用评估过程中，对材料塑性起始点(弹塑转变点)的确定尤为重要。

2、一般弹性变形与塑性变形的区别是：卸除载荷后，变形可以完全恢复是弹性变形的基本特征，而变形的不可恢复性是塑性变形的基本特征。弹性与塑性的基本区别不在于它们的应力-应变关系是否线性。普遍的方法是依据经验公式进行换算或材料本构模型公式拟合，然后人为判定得出塑性起始点，尤其是对于黏性的弹塑性塑料材料，经验和人为判定的差异非常大。

3、由上述可得，现有技术中，对于弹塑性固体材料的塑性起始点的确定方法存在精度不高的问题。

技术实现思路

1、本发明实施例提供一种塑性起始点的计算方法及装置，提高了确定弹塑性固体材料的塑性起始点的精度。

2、本技术实施例的第一方面提供了一种塑性起始点的计算方法，包括：

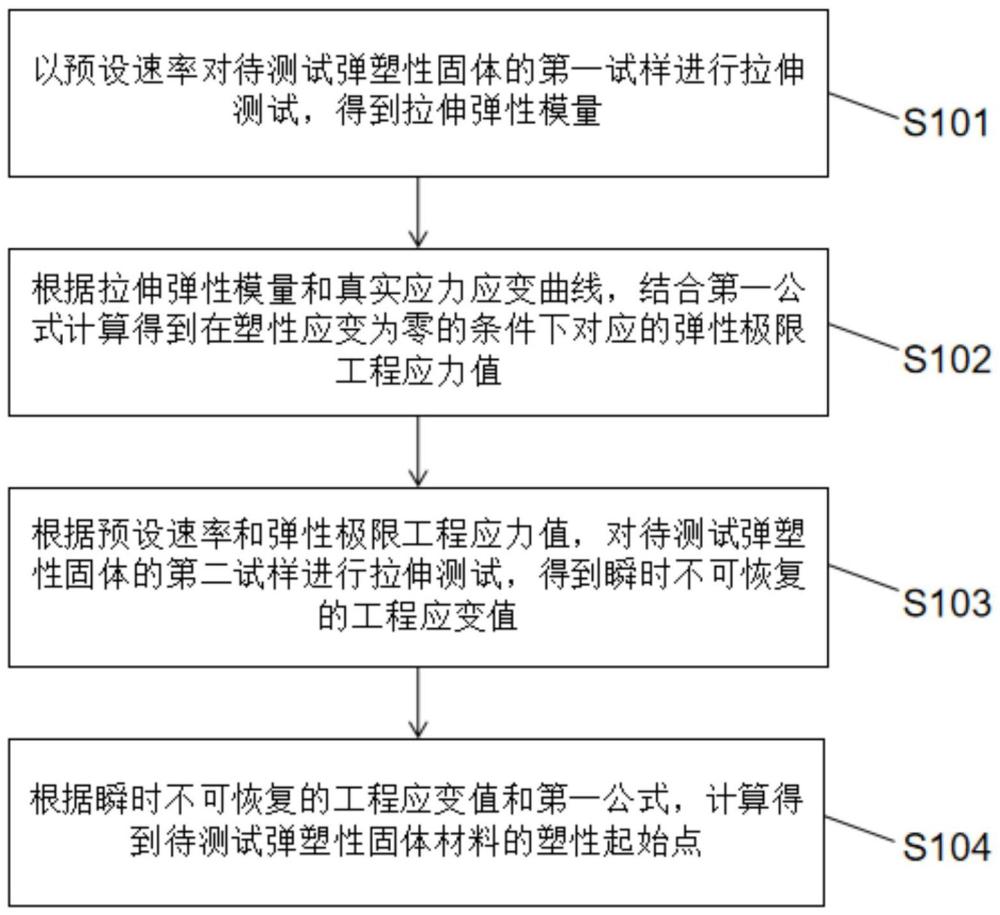
3、以预设速率对待测试弹塑性固体的第一试样进行拉伸测试，得到拉伸弹性模量；

4、根据拉伸弹性模量和真实应力应变曲线，结合第一公式计算得到在塑性应变为零的条件下对应的弹性极限工程应力值；

5、根据预设速率和弹性极限工程应力值，对待测试弹塑性固体的第二试样进行拉伸测试，得到瞬时不可恢复的工程应变值；

6、根据瞬时不可恢复的工程应变值和第一公式，计算得到待测试弹塑性固体材料的塑性起始点。

7、在第一方面的一种可能的实现方式中，以预设速率对待测试弹塑性固体的第一试样进行拉伸测试，得到拉伸弹性模量，具体为：

8、以预设速率对待测试弹塑性固体的第一试样进行拉伸测试，得到待测试弹塑性固体的第一试样的拉伸工程应力应变曲线；

9、根据拉伸工程应力应变曲线计算第一斜率后，将第一斜率作为拉伸弹性模量；其中，第一斜率为拉伸工程应力应变曲线的最小二乘回归线性拟合的斜率。

10、在第一方面的一种可能的实现方式中，真实应力应变曲线的计算过程具体为：

11、σt＝σe(1+εe)；

12、εt＝ln(1+εe)；

13、其中，σt和εt构成真实应力应变曲线；σe为工程应力；εe为工程应变；σt为真实应力；εt为真实应变。

14、在第一方面的一种可能的实现方式中，第一公式，具体为：

15、

16、其中，εp为塑性应变；σt和εt构成真实应力应变曲线；e为拉伸弹性模量。

17、在第一方面的一种可能的实现方式中，对待测试弹塑性固体的第二试样进行拉伸测试，得到瞬时不可恢复的工程应变值，具体为：

18、以预设速率将待测试弹塑性固体的第二试样的载荷加载至弹性极限工程应力值后，再以预设速率将待测试弹塑性固体的第二试样的载荷卸载至0，得到瞬时不可恢复的工程应变值。

19、在第一方面的一种可能的实现方式中，得到待测试弹塑性固体的第一试样的拉伸工程应力应变曲线，具体为：

20、根据预设实验参数调试试验机的拉伸测试程序；其中，预设实验参数包括：预设速率、间距、标距、和采集频率；

21、将待测试弹塑性固体的第一试样安装在试验机的夹具上，启动所拉伸测试程序，通过力值传感器记录待测试弹塑性固体的第一试样的载荷信息，通过引伸计测量待测试弹塑性固体的第一试样的标距段伸长，自动记录得到拉伸工程应力应变曲线。

22、本技术实施例的第二方面提供了一种塑性起始点的计算装置，包括：第一测试模块、获取模块、第二测试模块和计算模块；

23、其中，第一测试模块用于以预设速率对待测试弹塑性固体的第一试样进行拉伸测试，得到拉伸弹性模量；

24、获取模块用于根据拉伸弹性模量和真实应力应变曲线，结合第一公式计算得到在塑性应变为零的条件下对应的弹性极限工程应力值；

25、第二测试模块用于根据预设速率和弹性极限工程应力值，对待测试弹塑性固体的第二试样进行拉伸测试，得到瞬时不可恢复的工程应变值；

26、计算模块用于根据瞬时不可恢复的工程应变值和第一公式，计算得到待测试弹塑性固体材料的塑性起始点。

27、在第二方面的一种可能的实现方式中，以预设速率对待测试弹塑性固体的第一试样进行拉伸测试，得到拉伸弹性模量，具体为：

28、以预设速率对待测试弹塑性固体的第一试样进行拉伸测试，得到待测试弹塑性固体的第一试样的拉伸工程应力应变曲线；

29、根据拉伸工程应力应变曲线计算第一斜率后，将第一斜率作为拉伸弹性模量；其中，第一斜率为拉伸工程应力应变曲线的最小二乘回归线性拟合的斜率。

30、在第二方面的一种可能的实现方式中，真实应力应变曲线的计算过程具体为：

31、σt＝σe(1+εe)；

32、εt＝ln(1+εe)；

33、其中，σt和εt构成真实应力应变曲线；σe为工程应力；εe为工程应变；σt为真实应力；εt为真实应变。

34、在第二方面的一种可能的实现方式中，第一公式，具体为：

35、

36、其中，εp为塑性应变；σt和εt构成真实应力应变曲线；e为拉伸弹性模量。

37、相比于现有技术，本发明实施例提供的一种塑性起始点的计算方法及装置，所述方法包括：以预设速率对待测试弹塑性固体的第一试样进行拉伸测试，得到拉伸弹性模量；根据拉伸弹性模量和真实应力应变曲线，结合第一公式计算得到在塑性应变为零的条件下对应的弹性极限工程应力值；根据预设速率和弹性极限工程应力值，对待测试弹塑性固体的第二试样进行拉伸测试，得到瞬时不可恢复的工程应变值；根据瞬时不可恢复的工程应变值和第一公式，计算得到待测试弹塑性固体材料的塑性起始点。

38、其有益效果在于：本发明实施例根据待测试弹塑性固体的第一试样的拉伸弹性模量和真实应力应变曲线，结合第一公式计算得到在塑性应变为零的条件下对应的弹性极限工程应力值；根据预设速率和弹性极限工程应力值，对待测试弹塑性固体的第二试样进行拉伸测试，得到瞬时不可恢复的工程应变值；最后根据瞬时不可恢复的工程应变值和第一公式，计算得到待测试弹塑性固体材料的塑性起始点。本发明通过拉伸测试后，得到弹性极限工程应力值和瞬时不可恢复的工程应变值，并进一步根据瞬时不可恢复的工程应变值计算得到待测试弹塑性固体材料的塑性起始点，能够有效避免现有技术中由于人为判定塑性起始点而导致的精度不高的问题，本发明通过拉伸测试数据计算弹塑性固体材料的塑性起始点，保证了计算过程的客观性，有效提高了确定弹塑性固体材料的塑性起始点的精度。

39、进一步地，本发明思路新颖，结构简单，操作便捷，直指弹塑性力学本质；且通过静态拉伸测试和循环加载卸载测试之间的力学变形相关性，综合探究和分解材料力学特性，拓展了测试方法的应用。

40、再者，本发明结合理论公式与实际测试，从定义和变形机理出发，建立了塑性起始点的直接测试方法，填补了技术空白；结合理论知识与实际测试相结合，找出曲线关系，建立了材料弹塑性段辨别和对应的数据处理方法。

41、最后，本发明明确操作流程，大大提升了材料塑性起始点的直接测试装置及方法的可操作性。且本发明可推广应用于其他材料或压缩、剪切等其他力学性能的塑性起始点和弹塑性分段界定的直接测试，具有较高的普适性。