适用于壁挂炉的基于史密斯预估器的非线性内模控制方法

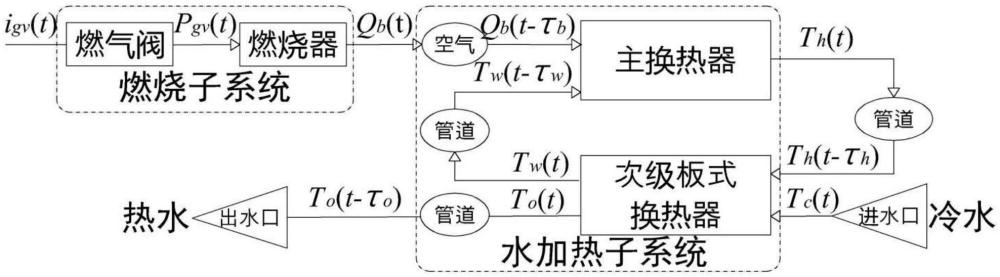
本发明涉及壁挂炉，具体涉及一种适用于壁挂炉的基于史密斯预估器的非线性内模控制方法。

背景技术：

1、随着“碳达峰、碳中和”要求的提出，燃气供给设施在中小城市进一步普及，燃气壁挂炉的市场需求也进一步扩大。近年来，我国燃气壁挂炉市场逐步从“普及型消费”向“舒适性消费”转变，着重从用户体验方向谋求产品升级。事实上，用户对产品舒适性的要求贯穿了燃气壁挂炉的整个发展历程。在人们不断追求高品质生活的今天，对舒适性的要求更是提升到了前所未有的高度。产品是否达到舒适性要求，甚至决定了燃气壁挂炉的市场命运。为响应世界节能减排号召、满足市场日益多元化的产品需求，喜德瑞集团作为欧洲领先的供热/热水设备制造商之一，从各方面对产品进行了质量提升，包括恒温控制、换热效率、燃烧噪音、保温时长、烟气处理、安全保障、使用寿命、产品外观等。其中，水温调节的快速性、稳定性和鲁棒性是影响用户舒适性的决定性因素之一，也是产品质量测评的重要指标。因此，燃气壁挂炉的温度控制技术理所当然地被放在了产品核心技术中的首要位置。

2、由于用户需求日益丰富，燃气壁挂炉衍生出了各种各样的产品型号，不同产品间的尺寸、功率、结构等都有较大差异，影响温度控制性能的因素更加复杂。为实现精确的水温控制，基于工程经验改进的传统pid控制算法日趋复杂臃肿。尽管控制算法的计算量倍增，但仍旧难以满足各种不同容量、功率、结构产品在不同工况下的恒温控制系统高性能要求，亟需设计更加简洁高效的先进控制算法替代传统的工程pid算法。

3、基于上述情况，本发明提出了一种适用于壁挂炉的基于史密斯预估器的非线性内模控制方法，可有效解决以上问题。

技术实现思路

1、本发明的目的在于提供一种适用于壁挂炉的基于史密斯预估器的非线性内模控制方法。本发明的适用于壁挂炉的基于史密斯预估器的非线性内模控制方法嵌入了三种控制技术：反馈线性化控制、基于史密斯预估器的控制和内模控制，分别用于处理系统非线性、时延、模型参数变化及外部干扰的影响。该方案能够有效保证壁挂炉系统在复杂工况下温度控制的精确性和稳定性，既能合理抵消系统非线性和时延对闭环系统稳定性的影响，又能灵活适应系统参数的大幅度变化、充分消除模型不确定性和外部干扰对控制精度的影响，最终保证整个温度控制系统的安全可靠运行。此外，本发明提供了完备的控制参数整定方案，只一个待调节参数。

2、本发明通过下述技术方案实现：

3、适用于壁挂炉的基于史密斯预估器的非线性内模控制方法，包括：

4、步骤s1：总结两用型燃气壁挂炉系统dhw模式下的热传递过程，建立非线性模型；

5、步骤s2：使用反馈线性化方法将非线性模型转换为线性模型，以处理执行器非线性的对闭环系统稳定性的影响；

6、步骤s3：对线性模型设计基于史密斯预估器的控制结构，以处理时延对闭环系统的影响；

7、步骤s4：基于内模控制原理推导出参数整定方法；

8、步骤s5：对闭环系统进行稳定性分析；

9、步骤s6：基于测试数据，获得线性模型的各部分辨识结果；

10、步骤s7：对水温调节系统进行冷启动测试、停水测试和水流量变化测试。

11、本发明的适用于壁挂炉的基于史密斯预估器的非线性内模控制方法嵌入了三种控制技术：反馈线性化控制、基于史密斯预估器的控制和内模控制，分别用于处理系统非线性、时延、模型参数变化及外部干扰的影响。该方案能够有效保证壁挂炉系统在复杂工况下温度控制的精确性和稳定性，既能合理抵消系统非线性和时延对闭环系统稳定性的影响，又能灵活适应系统参数的大幅度变化、充分消除模型不确定性和外部干扰对控制精度的影响，最终保证整个温度控制系统的安全可靠运行。此外，本发明提供了完备的控制参数整定方案，只一个待调节参数。

12、优选的，所述步骤s1具体步骤包括：

13、步骤s11：在忽略燃气阀调节和燃烧过程的瞬时动态，并忽略燃气阀回程的微小偏差的情况下，热功率qb(t)与燃气压力pgv(t)之间的关系满足：

14、

15、其中，ζ可被视为一个近似恒定的系数，与燃气的热值、喷嘴系数、喷嘴直径以及燃气的相对密度有关；

16、步骤s12：燃气压力pgv(t)与驱动电流igv(t)之间的非线性关系可以近似表示为：

17、

18、其中，imin与imax分别是燃气阀最小和最大的操作电流，pmin与pmax分别是燃气阀可供给的最小和最大燃气压力，iop和ist分别对应着燃气阀的实际开启电流和到达饱和时的电流，c1、c2、c3为常值系数；

19、步骤s13：忽略内部水流循环过程中的微小能量损失，即假设tω(t)＝tω(t-τh-τω)，水加热系统的能量守恒方程可被概括为：

20、

21、其中，η是燃烧过程的热转换效率，ρ(kg/m3)是水的密度，m(kg)是次级板换中生活水容量的质量(与wf成线性关系)，ce(j/kg·℃)是水的比热容；

22、步骤s14：将x(t)＝to(t)-tc视为系统状态，igv(t)视为主动输入(即控制信号)，并将tc视为被动输入(即负载)，综合式(1)～(3)，可推导出两用型壁挂炉系统在dhw模式下的非线性模型：

23、

24、其中，τ＝τb+τh且

25、请注意，用于测量to的温度传感器位于次级板式换热器的出口处，τh与水流速率wf成线性关系，tc这一项可以被视为y(t)的初始值。

26、优选的，所述步骤s2具体步骤包括：

27、步骤s21：由于存在f(·)，为了线性化非线性模型，这里引入一个中间控制信号vm，其定义为vm(t)＝f[igv(t)]；vm的物理含义是气体压力的平方根值，即此外，定义模型参数α＝ρwf/m和β＝ηζ/mce，则可以将(4)改写为：

28、

29、若水流速wf不变，则参数α和β为定常数，故在水流速wf不变的情况下，通过上述反馈线性化过程，非线性模型被转化为了线性模型；

30、步骤s22：当针对线性模型设计的控制信号确定后，作用于真实非线性模型的物理控制信号，即燃气阀电流，应通过下式计算：

31、igv(t)＝finv[vm(t)]＝f-1[vm(t)]  (6)

32、其中，f(·)和finv(·)通过系统辨识获得。

33、优选的，所述步骤s3的具体步骤为：

34、步骤s31：对线性模型进行拉普拉斯变换：

35、

36、其中，x(s)、y(s)和vm(s)分别是x(t)、y(t)和vm(t)的s域形式；

37、步骤s32：基于此，在零初始条件下，线性模型的传递函数可以提取为：

38、

39、其中，km＝β/α＝η/(ζρcewf)且hm＝1/α＝m/(ρwf)；

40、步骤s33：将gm(s)分解为纯时延部分e-τs和无时延部分gm0：

41、

42、步骤s34：基于由系统辨识获得的模型(2)、(8)以及无时延模型(9)，设计一个基于史密斯预估器的控制结构，史密斯预估器的传递函数可归纳为：

43、gsp(s)＝gm0(s)-gm(s)＝gm0(s)(1-e-τs)   (10)

44、其中，用于预估器计算的模型参数(km，hm以及时延τ)是基于系统辨识结果和水流速测量值wf实时计算的；

45、反馈控制器c(s)的设计如下：

46、

47、其中，kp和ki分别是控制器的比例增益和积分增益。

48、优选的，所述步骤s4具体步骤为：

49、步骤s41：基于史密斯预估器的控制结构与imc结构的等效条件是设计c(s)使得下式成立：

50、

51、步骤s42：由此可推导出，要使基于史密斯预估器的控制结构具有经典imc结构的等效特性，即模型适应和干扰抑制能力，控制器c(s)需满足：

52、

53、步骤s43：为一阶时延模型(8)设计该等效内模控制器cimc(s)，模型(8)可以被因式分解为gm(s)＝gm0(s)e-τs，其中gm0是一阶最小相位系统；理想情况下，内模控制器cimc(s)应当是gm0(s)的逆，由此可使闭环系统在gp(s)＝gm(s)时满足y(s)/tset(s)＝1，从而实现参考信号的完美跟踪；然而，由于是非真的，即控制器是物理不可实现的；

54、因此，这里在cimc(s)中进一步引入了一阶滤波器q(s)＝1/(λs+1)，λ为滤波器时间常数，从而将控制器cimc(s)转换为半真模型；综上，控制器cimc(s)的最终形式为：

55、

56、步骤s44：结合(13)与(14)可得控制器c(s)的具体期望形式为：

57、

58、步骤s45：结合控制器c(s)的原始形式(11)与期望形式(15)，推导出比例系数kp和积分系数ki的自整定方案：

59、

60、其中，模型参数km，hm和τ应基于系统辨识结果和水流速测量值wf实时计算，会随着水流速wf的波动而变化。

61、优选的，所述步骤s5的具体步骤为：

62、步骤s51：由于基于史密斯预估器的控制结构的传递函数如下：

63、

64、因此，闭环系统满足：

65、

66、其中，d(s)表示d(t)在s域中的形式；

67、步骤s52：设gp(s)中的无时延部分为gp0(s)(即gm0(s)对应的真实模型)，系统的真实时延为τp(即总时延τ的真实值)，将(15)、(17)代入(18)可得：

68、

69、从公式(19)和(20)中可以看出，如果gm≈gp，则闭环系统可以分解为一个无时延部分cgp0/[1+c(gm0-gm+gp)]和一个纯时延部分

70、因为当所以从(19)和(20)可以推断出：

71、

72、即s→0时，输出y(s)将到达tset(s)，且干扰d(s)对输出y(s)的影响为0；

73、步骤s53：将系统非线性finv和f的模型误差视为模型不确定性和外部干扰的一部分，则结合最终值定理，由(19)可知，如果输入信号tset(t)和d(t)是有界且稳定的，即使存在时延、模型不确定性、外部干扰以及由于wf变化引起的参数变化，随着t→∞，系统输出y(t)＝to(t)依然将准确达到设定值tset，且干扰对输出的影响将被彻底消除。

74、优选的，所述步骤s6的具体步骤为：

75、步骤s61：在水流量不变时，v(t)＝pb(t)＝f[igv(t)]到to(t)的传递函数可概括为：

76、

77、其中，km＝β/α＝η/(ζρcewf)且hm＝1/α＝m/(ρwf)；

78、步骤s62：基于测试数据，利用matlab的curve fitting工具箱进行拟合，获得系统模型的各部分辨识结果：

79、

80、τ≈2.04s。

81、本发明与现有技术相比，具有以下优点及有益效果：

82、1、提供了两用壁挂炉系统生活热水模式下的多工况建模方法，该方法综合考虑了执行器非线性、系统参数随水流量变化、时延等复杂因素。

83、2、对系统模型参数进行辨识，有效提高模型精度、增强控制质量。

84、3、嵌入了反馈线性化控制技术，有效处理了执行器非线性对温度控制稳定性的影响。

85、4、嵌入了基于史密斯预估器的控制技术，有效处理了变化的大时延对温度控制稳定性的影响。

86、5、嵌入了内模控制技术，能灵活适应系统参数的大幅度变化，充分消除模型不确定性和外部干扰对控制精度的影响，有效保证了系统在冷热启动、水流速大幅度变化等恶劣工况下温度控制的稳定性和精确性。

87、6、基于内模控制原理设计了完备的参数整定方案，仅一个待调节参数，极大地减少了控制参数数量，降低了一线调试人员的工作量，提升了产品的智能化程度。

88、7、严谨分析了所设计的闭环系统的稳定性、控制精度和抗干扰性能。整个控制方案有效提高了燃气壁挂炉系统的温度收敛速度和稳态控制精度等关键指标。