一种风力发电机组载荷重构方法与流程

本发明涉及风力发电机组在线监测，特别涉及一种风力发电机组载荷的重构方法。

背景技术：

1、在风力发电机组在线监测领域，风力发电机组的载荷变化对于机组的安全运行至关重要。现有的载荷监测和重构方法由于成本高昂、设备复杂，尚未得到广泛应用。实际运行中，载荷会受到多种不确定性因素的影响，这使得载荷的规律变化非常复杂。因此，对载荷的监测和分析对确保机组的安全运行和运维具有重要意义。

2、现有技术主要采用两种载荷重构方法：一是利用实测载荷和机器学习方法相结合的预测方法；二是结合物理模型和scada数据的仿真计算方法。前者面临数据稀缺和成本高的问题，而后者虽然拥有大量的scada系统运行数据，但由于运行工况的复杂性，缺乏准确的运行工况和运行边界数据(如风廓线、湍流风速)，导致重构精度受到不确定性的影响。

3、因此，有必要开发一种新型的能够有效实现载荷快速计算，且考虑多源不确定的风力发电机组载荷重构方法。

技术实现思路

1、本发明的目的是提供一种风力发电机组载荷重构方法，以实现风力发电机组载荷的快速计算，并预测结果的置信度，将其应用于风力发电机组的在线监测和运维中。

2、根据本发明的第一方面，提供一种风力发电机组载荷重构方法，其特征在于，包括以下步骤：

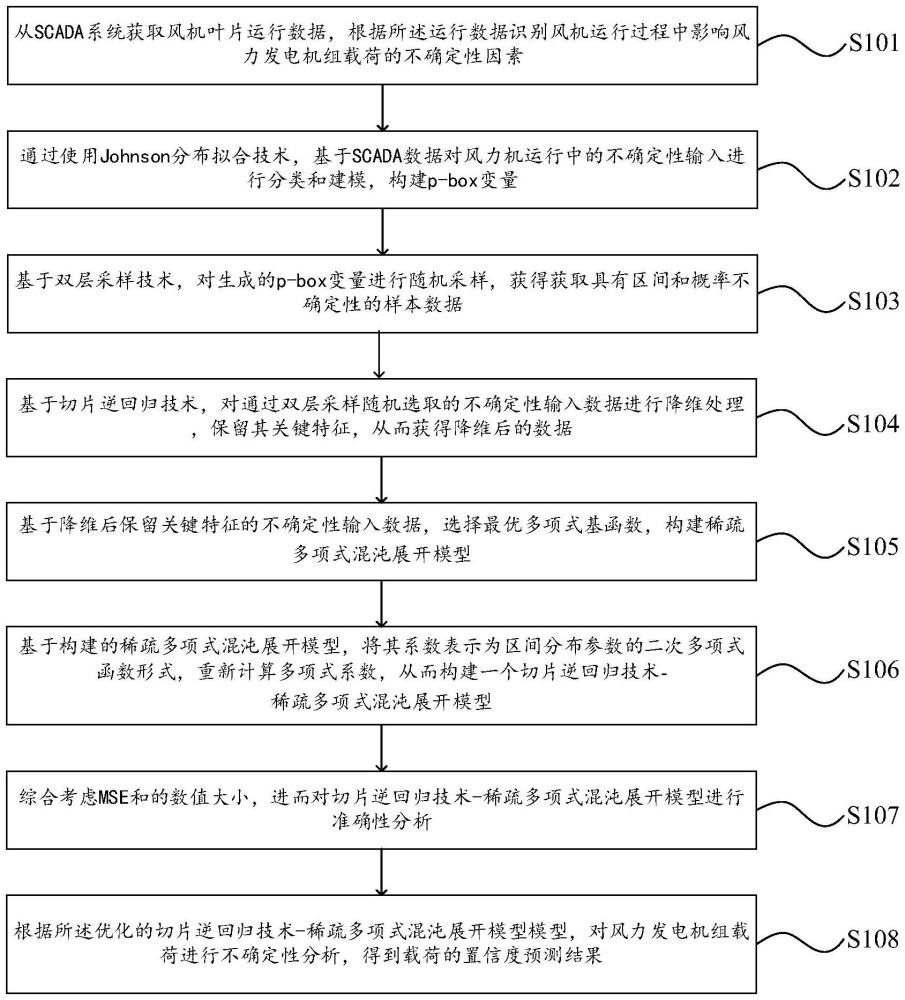
3、从scada系统获取风机叶片运行数据，根据所述运行数据识别风机运行过程中影响风力发电机组载荷的不确定性因素；

4、通过使用johnson分布拟合技术，基于scada数据对风力机运行中的不确定性输入进行分类和建模，构建p-box变量，以准确描述不确定性因素对风力发电机组载荷的影响；

5、基于双层采样技术，对生成的p-box变量进行随机采样，获得获取具有区间和概率不确定性的样本数据，所述样本数据包含风速、风向角、温度、湍流风速和风廓线；

6、基于切片逆回归技术，对通过双层采样随机选取的不确定性输入数据进行降维处理，保留其关键特征，从而获得降维后的数据；

7、基于降维后保留关键特征的不确定性输入数据，选择最优多项式基函数，构建稀疏多项式混沌展开模型；

8、基于构建的稀疏多项式混沌展开模型，将其系数表示为区间分布参数的二次多项式函数形式，重新计算多项式系数，从而构建一个切片逆回归技术-稀疏多项式混沌展开模型；

9、综合考虑mse和r2的数值大小，进而对切片逆回归技术-稀疏多项式混沌展开模型进行准确性分析，通过调整模型的多项式阶数p和基函数数量，以优化模型的精度和计算效率的最佳平衡；

10、根据所述优化的切片逆回归技术-稀疏多项式混沌展开模型模型，对风力发电机组载荷进行不确定性分析，得到载荷的置信度预测结果。

11、如上所述的方面和任一可能的实现方式，进一步提供一种实现方式，所述运行数据包括风速、风向、温度以及转速；

12、所述影响风力发电机组载荷的不确定性因素包括稳态风速、湍流风速、风向角以及温度。

13、如上所述的方面和任一可能的实现方式，进一步提供一种实现方式，所述基于双层采样技术，对生成的p-box变量进行随机采样，获得获取具有区间和概率不确定性的样本数据，所述样本数据包含风速、风向角、温度、湍流风速和风廓线，包括：

14、使用拉丁超立方体采样(lhs)方法生成个外层样本θ(w)＝(θ1(w),θ2(w),...,θn(w)),其中下标1,2，...n表示不确定性输入变量的数量，每个样本表示不确定性输入的区间分布参数；

15、对于外层的每个样本θ(w)，采用稀疏插值配置点方法选择有效的样本点，生成内层样本ξ，具体采用稀疏插值值配置点方法的稀疏插值：

16、

17、其中，表示张量积，ι表示配置水平，|i|＝i1+i2+...in表示多指标的和，表示第ik维的配置点，其可以通过高斯求积或者clenshaw-curtis规则获得；

18、然后从稀疏插值点集合ξ中选择m个样本点x(v)＝(x1(v),x2(v),...,xn(v))，其中v＝1,2，...,m用于线性回归计算；为了获得稳定性的结果，样本点数m需大于或等于多项式系数的2倍，即m≥2q。。

19、如上所述的方面和任一可能的实现方式，进一步提供一种实现方式，其中，采用切片逆回归技术的关键计算如下：

20、采用双层采样生成的样本数据，作为不确定输入参数输入到气-弹-机-电耦合模型计算得到输出响应y；

21、对每个输入变量进行标准化处理，使其均值为零、方差为1，计算标准化后的输入矩阵x(v)的协方差矩阵

22、

23、其中x1(i)为第x1(v)个输入变量，为输入数据的均值向量，m为样本数；

24、将输出响应y分成h个切片，每个切片内的样本数量为nh(v)，对于每个切片，计算输入变量的切片均值mh(v)：

25、

26、其中，sh(v)表示属于第h个切片的样本集合，j表示切片sh的样本索引；

27、使用切片均值计算协方差矩阵γ(v)，该矩阵反映了切片之间的差异：

28、

29、通过解广义特征值问题γβ＝λξβ，求解特征值λ和特征向量β；

30、其中，特征向量β是切片逆回归方法的有效维数回归方向，反映了最具代表性的低维特征方向；

31、选择具有最大特征值的前q个特征向量β1，β2，...，βq，将高维输入数据x(v)投影到低维空间，得到降维后的数据矩阵z(v)＝(z1(v),z2(v),...,zq(v))，其中每个zi是独立的变量：

32、z＝xb

33、其中，b＝[β1,β2,...,βq]是由选定特征向量组成的矩阵。

34、如上所述的方面和任一可能的实现方式，进一步提供一种实现方式，所述构建的稀疏多项式混沌展开模型表示为：

35、

36、其中，y(t)表示风力发电机组载荷随时间t的变化，z表示基于sir算法处理后的输入变量，表示与xi最相关的多项式基函数，表示多项式系数。

37、如上所述的方面和任一可能的实现方式，进一步提供一种实现方式，最终构建的切片逆回归技术-稀疏多项式混沌展开模型为：

38、

39、其中，表示多项式系数，表示与zi最相关的多项式基函数，即最优多项式基函数，q是多项式展开阶数，n是不确定性输入变量的总数量，θ表示外层分布变量，ai,0、bi,j、di,j是二次多项式的系数。

40、如上所述的方面和任一可能的实现方式，进一步提供一种实现方式，所述综合考虑mse和r2的数值大小，进而对切片逆回归技术-稀疏多项式混沌展开模型进行准确性分析，通过调整模型的多项式阶数p和基函数数量，以优化模型的精度和计算效率的最佳平衡，包括：

41、计算第一输出载荷的均值；

42、将已将通过双层采样策略和切片逆回归技术生成了的降维后的不确定性输入数据输入到切片逆回归技术-稀疏多项式混沌展开模型，得到第二输出载

43、^

44、荷y；

45、基于以下式子分别计算均方误差mse和判定系数r2：

46、

47、其中，是第二输出载荷，yi是第一输出载荷，是第一输出载荷的均值。

48、相比于现有技术，本发明具有以下有益效果：

49、(1)传统方法往往依赖于精确的输入数据，但在实际操作中，由于环境条件、设备状态等多种因素的复杂性，获取精确的数据通常较为困难。本发明通过引入不确定性建模技术，采用johnson分布拟合技术和p-box建模成功解决了在实际运行的仿真分析中输入参数难以精确量化的问题。通过结合切片逆回归(s ir)技术和稀疏混沌多项式展开(spce)技术，本发明能够有效降维并保留输入数据的关键特征，同时量化这些不确定性因素，显著提高了载荷计算的准确性和可靠性；

50、(2)本发明在载荷重构过程中，能够提供不同置信度水平下的预测结果置信区间，使得决策者在实际应用中可以根据不同的置信度等级做出更为可靠的运维决策，从而有效提升风力发电机组运行的安全性和稳定性；

51、(3)本发明通过结合切片逆回归(sir)和稀疏混沌多项式展开(spce)技术，成功解决了传统pce方法在处理高维输入空间时常遇到的“维数灾难”问题。随着输入变量的增多，传统方法通常导致多项式项数量急剧增加，计算负担过重。通过sir技术的降维和对关键特征的选取，本发明构建了一个更加紧凑且高效的代理模型，显著提升了模型的计算效率和预测能力。因此，本发明的方法突破了传统pce的局限，为风电领域的不确定性分析提供了创新且高效的解决方案。

52、应当理解，技术实现要素：部分中所描述的内容并非旨在限定本发明的实施例的关键或重要特征，亦非用于限制本发明的范围。本发明的其它特征将通过以下的描述变得容易理解。